Содержание
- 2. Цель работы Техническая цель работы: практическое освоение принципов дискретно-цифрового автоматического управления непрерывным объектом. Для этой цели
- 3. 2. Учебное задание а) Разработка математической модели по функциональной и принципиальной схемам системы. б) Ознакомление с
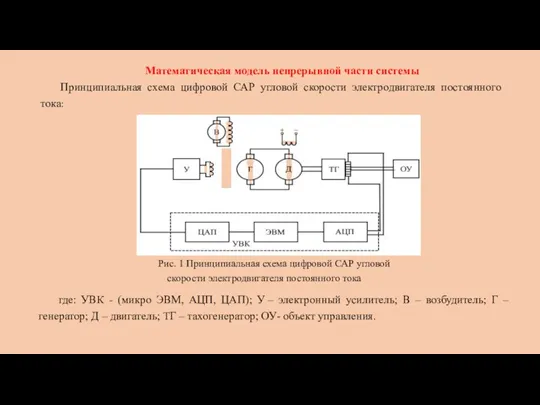
- 4. Математическая модель непрерывной части системы Принципиальная схема цифровой САР угловой скорости электродвигателя постоянного тока: где: УВК
- 5. Рис. 2 Функциональная схема цифровой САР угловой скорости электродвигателя постоянного тока Функциональная схема и числовые значения
- 6. Передаточные функции объекта регулирования (двигателя совместно с рабочим механизмом) по регулирующему и задающему воздействиям соответственно Передаточная
- 7. Передаточная функция исполнительного органа 2 (генератора)
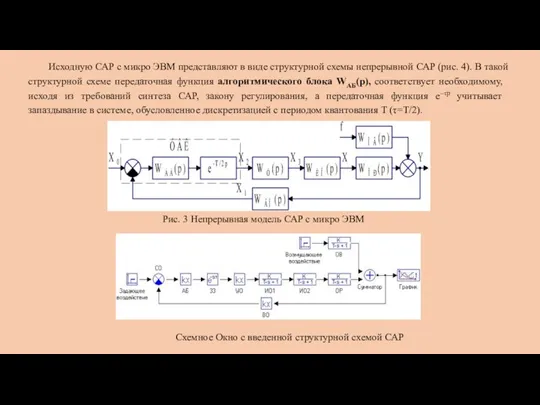
- 8. Исходную САР с микро ЭВМ представляют в виде структурной схемы непрерывной САР (рис. 4). В такой
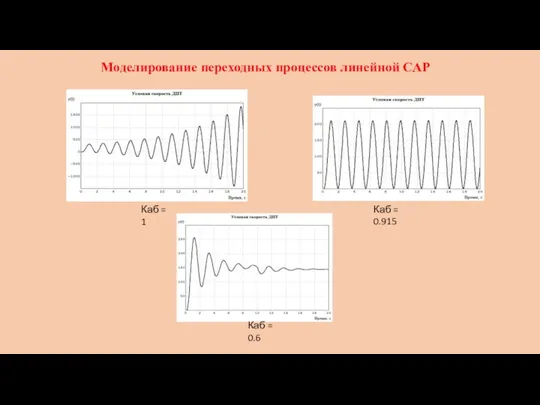
- 9. Моделирование переходных процессов линейной САР Каб = 1 Каб = 0.915 Каб = 0.6
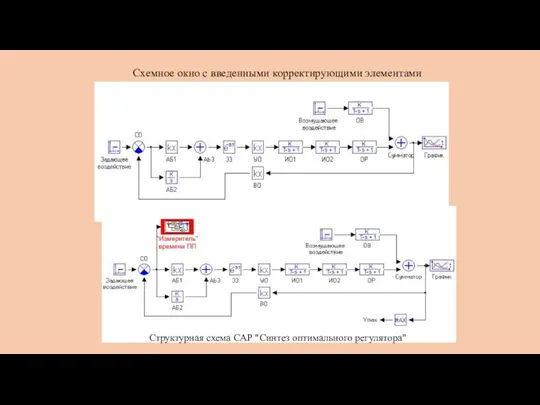
- 10. Схемное окно с введенными корректирующими элементами Структурная схема САР "Синтез оптимального регулятора"
- 11. Запускаем задачу на расчет с новыми значениями kab1=0,1025; kab2=0,08726 Запускаем задачу на расчет с новыми значениями
- 12. Моделирование переходных процессов САР с дискретным регулятором
- 13. Структурная схема непрерывно-дискретной модели САР с ПИ-регулятором Диалоговое окно блока Дискретная передаточная функция общего вида "АБ(z)"
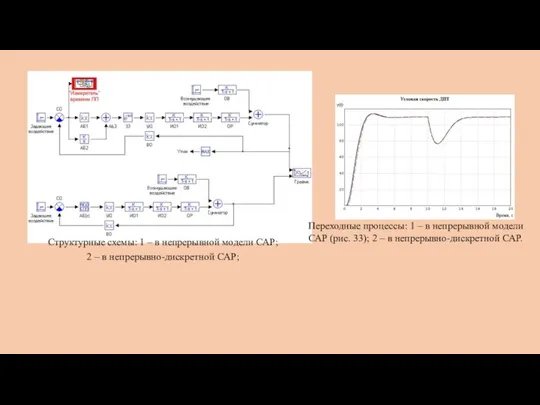
- 14. Структурные схемы: 1 – в непрерывной модели САР; 2 – в непрерывно-дискретной САР; Переходные процессы: 1
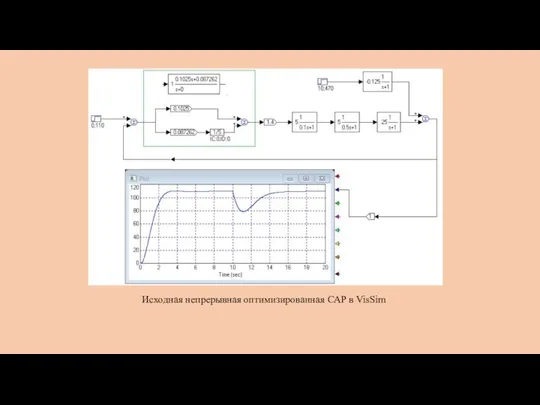
- 15. Исходная непрерывная оптимизированная САР в VisSim
- 16. Замена непрерывного регулятора дискретным в VisSim'е. Для выбора периода дискретизации нужно обратиться к постоянным времени объекта
- 17. Аналоговая и дискретная модель ПИ-регулятора Выбранный период дискретизации, равный 0.001 сек обеспечивает полную эквивалентность САР с
- 18. Тем не менее, полезно посмотреть на поведение САР и при больших значениях периода дискретизации, что позволит
- 19. Определение алгоритма работы цифрового регулятора На цифровой регулятор подается непрерывный сигнал ошибки с устройства сравнения (сумматора).
- 20. Ниже приведен пример получение формулы вычисления значений решетчатой функции выходного сигнала дискретного регулятора Полученная формула указывает
- 22. Скачать презентацию













 История развития Интернета
История развития Интернета Пакет подготовки презентаций Microsoft Power Point
Пакет подготовки презентаций Microsoft Power Point Кодирование информации
Кодирование информации Помехоустойчивое кодирование
Помехоустойчивое кодирование Диагностика по CAN
Диагностика по CAN i-Genius: School Management ERP Software
i-Genius: School Management ERP Software Введение в тестирование
Введение в тестирование Технология мультимедиа
Технология мультимедиа Способы записи алгоритмов
Способы записи алгоритмов Управление внедрением систем
Управление внедрением систем Cisco CCNA and CCNP
Cisco CCNA and CCNP Архитектура ORACLE. Установление соединения по сети
Архитектура ORACLE. Установление соединения по сети Технологии реализации интерфейсов
Технологии реализации интерфейсов Решение задания повышенного уровня сложности С1 (3 балла)
Решение задания повышенного уровня сложности С1 (3 балла) Основы искусственных нейтронных сетей
Основы искусственных нейтронных сетей Компьютерные игры в культурном контексте: от классического понимания до постмодерна
Компьютерные игры в культурном контексте: от классического понимания до постмодерна Сравнительный анализ сайтов
Сравнительный анализ сайтов YouTube
YouTube День информатики
День информатики История и возможности социальной сети
История и возможности социальной сети Множество. Повторение. 3 класс
Множество. Повторение. 3 класс Делегаты в C#
Делегаты в C# Информационно-технологическая инфраструктура организации. Программное обеспечение
Информационно-технологическая инфраструктура организации. Программное обеспечение Профилактика киберпреступлений и борьба с ними
Профилактика киберпреступлений и борьба с ними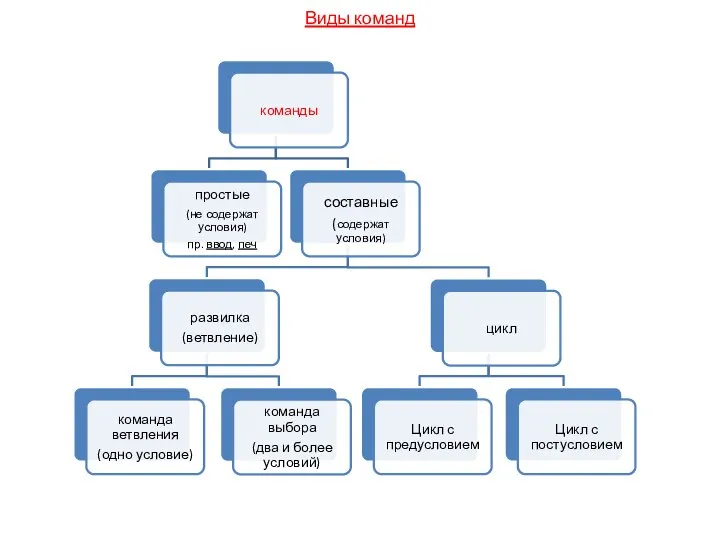 Основные виды команд
Основные виды команд Введение в блокчейн
Введение в блокчейн Защита моего ПК
Защита моего ПК Библиотека – чудесная страна
Библиотека – чудесная страна