Содержание
- 2. Переводы из двоичной: 11010010101001010010100102 = ?16 1101001010100101001010010 СТРОГО СПРАВА!!! 000 А2 = А16 1 A 5
- 3. Переводы из двоичной 11010010101001010010100102 = ?8 1101001010100101001010010 СТРОГО СПРАВА!!! 00 А2 = А8 1 5 1
- 4. Переводы из двоичной 11010010101001010010100102 = ?4 1101001010100101001010010 СТРОГО СПРАВА!!! 0 А2 = А4 1 2 2
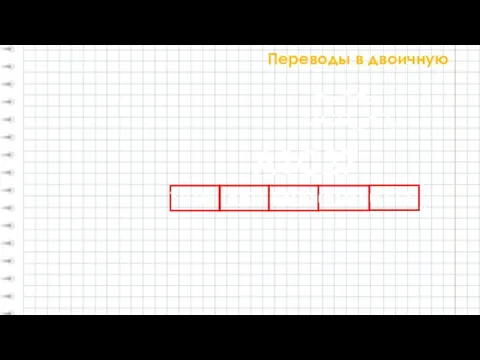
- 5. Переводы в двоичную A1C2716 = ?2 А16 = А2 0001 1010 2 A1C27 1100 0010 0111
- 6. Переводы в двоичную 734678 = ?2 А8 = А2 011 111 2 73467 100 110 111
- 7. Переводы в двоичную 12231314 = ?2 А4 = А2 2 1223131 01 11 01 11 10
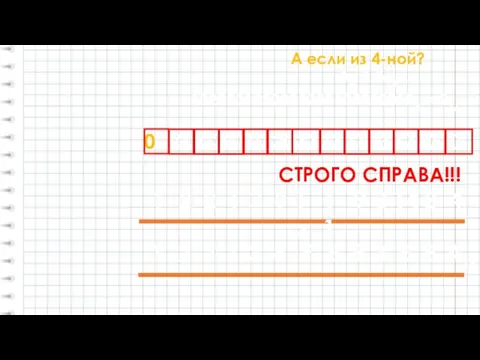
- 8. А если из 4-ной? 10202010220332321033220104 = ?16 1020201022033232103322010 СТРОГО СПРАВА!!! 0 А4 = А16 1 2
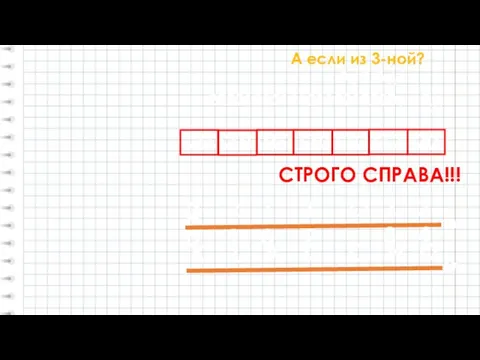
- 9. А если из 3-ной? 2022101011101102122203 = ?27 202210101110110212220 СТРОГО СПРАВА!!! А3 = А27 20 10 21
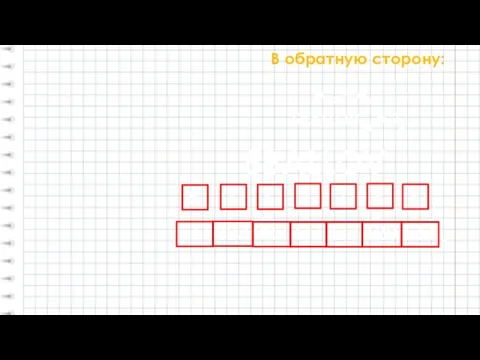
- 10. В обратную сторону: 18256389 = ?3 А9 = А3 3 1825638 22 10 20 12 02
- 11. В обратную сторону: 5BALLOV64 = ?4 А64 = А4 10 5BALLOV 31 24 21 21 10
- 12. Системы с нестандартным принципом перехода через разряд Обычно: 135 7 Принцип: Наполнение каждого разряда по 7
- 13. А если взять совсем другой принцип?: 135 ы Принцип: В мешки – по 6, в телеги
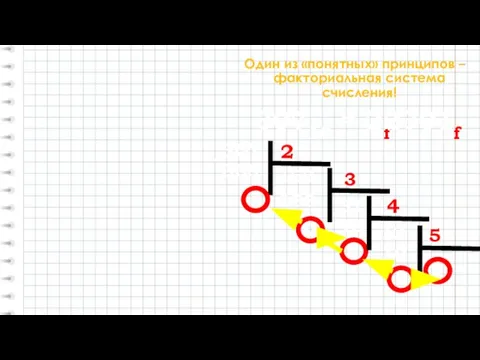
- 14. Один из «понятных» принципов – факториальная система счисления! 2321f = 1! 2! 3! 4! =2×4!+3×3!+2×2!+1×1!= =48+18+4+1=71
- 15. Один из «понятных» принципов – факториальная система счисления! 30710 = ?f 1 2 0 3 51
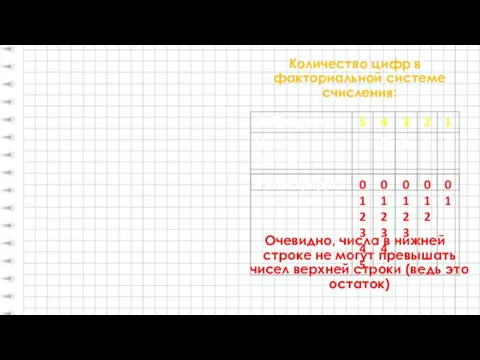
- 16. Количество цифр в факториальной системе счисления: Очевидно, числа в нижней строке не могут превышать чисел верхней
- 17. Количество цифр в факториальной системе счисления: 54321f - возможно 12345f - невозможно 30221f - 10422f -
- 18. Фибоначчиева система счисления Алфавит: только цифры 0 и 1 Числа Фибоначчи нумеруют разряды: 1, 2, 3,
- 19. Фибоначчиева система счисления 10101fib= 1 2 3 5 =1×8+0×5+1×3+0×2+1×1= =8+3+1=12 8
- 20. Фибоначчиева система счисления! 32510 = ?fib 32510 = 101000000100fib Выписываем числа Фибоначчи справа налево: … 377,
- 21. Ещё один пример: 8710 = ?fib 8710 = 101010100fib Выписываем числа Фибоначчи справа налево: … 144,
- 22. Проблемная зона 100fib = 310 11fib = 310 Правило: В Фибоначчиевой СС строго ЗАПРЕЩЕНО ставить две
- 23. Пожалуйста, выполните тестирование №1 и №2.
- 24. Слайд для записей
- 25. Подготовка к контрольной работе (на следующем занятии) Переводы в 10СС и обратно (с дробями) Арифметические действия
- 26. Нестандартная задача №1: Перечислите по возрастанию все основания систем счисления, в которых запись числа 3110 оканчивается
- 27. Задания других типов: Перечислите по возрастанию все основания систем счисления, в которых запись числа 2710 оканчивается
- 28. Задания других типов: Перечислите по возрастанию все числа (в 10-ичной системе), не превосходящие 31, запись которых
- 29. Задания других типов: Перечислите по возрастанию все числа (в 10-ичной системе), не превосходящие 50, запись которых
- 30. Задания других типов: Дано А=В816 и В=2728 Найдите такое С (в 2-ичной системе), что А Переведём
- 31. Задания других типов: Самостоятельно: Дано А=22223 и В=1228 Найдите такое С (в 2-ичной системе), чтобы оно
- 32. Задания других типов: А также, быстрые переводы: Переведите двоичное число в 16-ичную систему: 1110111011101110...1110 (40 знаков)
- 33. Ну и сюрпризы тоже будут
- 34. Пожалуйста, выполните последнее тестирование. Для его выполнения, создайте, пожалуйста, отдельную вкладку в браузере, чтобы не «потерять»
- 35. Слайд для записей
- 37. Скачать презентацию




























 Модель черного ящика
Модель черного ящика Информационно-аналитическая система SCIENCE INDEX
Информационно-аналитическая система SCIENCE INDEX Графы. Общие понятия
Графы. Общие понятия Уровни программной конфигурации ПК
Уровни программной конфигурации ПК Временные ограничения цифровых схем
Временные ограничения цифровых схем Разработка программы для проектирования плана города
Разработка программы для проектирования плана города 5_Arrays_Lubchenko
5_Arrays_Lubchenko Vom Modell zur relationalen Datenbank
Vom Modell zur relationalen Datenbank Как воспользоваться электронной книгой. 1 - Виды форматов электронных книг 2- Программы для чтения электронных книг 3- Как скача
Как воспользоваться электронной книгой. 1 - Виды форматов электронных книг 2- Программы для чтения электронных книг 3- Как скача Integer Programming Example #1 - Combinatorics
Integer Programming Example #1 - Combinatorics Моделирование, формализация. Визуализация
Моделирование, формализация. Визуализация Операции с изображением на уровне растра
Операции с изображением на уровне растра Методы и средства сбора, передачи, хранения и поиска информации
Методы и средства сбора, передачи, хранения и поиска информации Контактный центр будущего
Контактный центр будущего Творческая работа на уроке информатики
Творческая работа на уроке информатики Электронные таблицы. Обработка числовой информации в электронных таблицах
Электронные таблицы. Обработка числовой информации в электронных таблицах Текст как информационный объект. Автоматизированные средства и технологии организации текста
Текст как информационный объект. Автоматизированные средства и технологии организации текста Естественные и искусственные источники информации. 3 класс
Естественные и искусственные источники информации. 3 класс Популяризация внутреннего туризма в РФ через внедрение современных медийных и репортажных технологий
Популяризация внутреннего туризма в РФ через внедрение современных медийных и репортажных технологий Информационная безопасность
Информационная безопасность Цикл с параметром в Pascal. Lazarus
Цикл с параметром в Pascal. Lazarus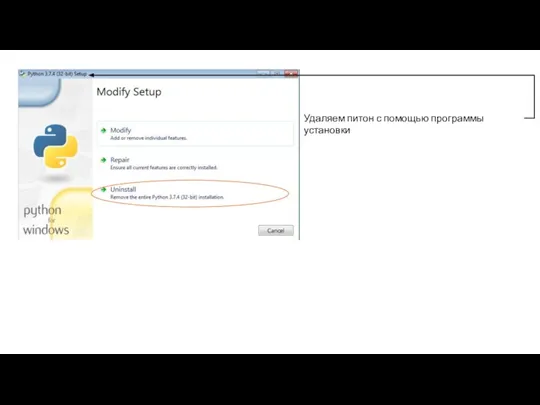 Как установить Пайчарм
Как установить Пайчарм Презентация на тему Охрана труда и техника безопасности
Презентация на тему Охрана труда и техника безопасности 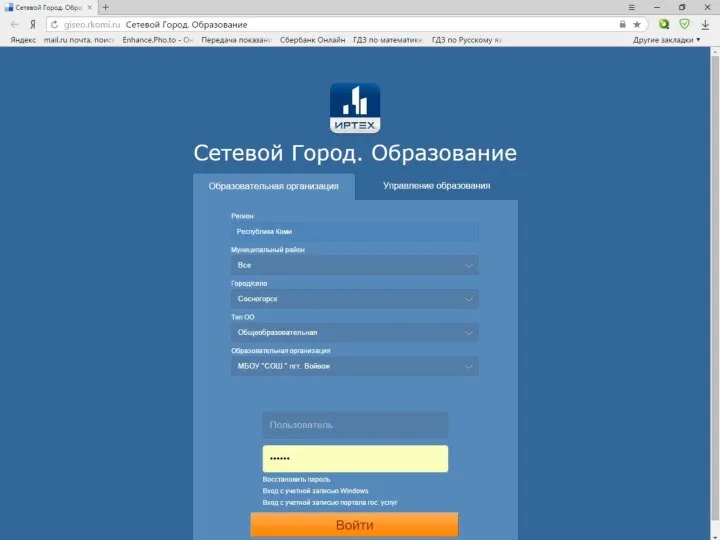 Сетевой город. Образование
Сетевой город. Образование Написание программы
Написание программы Современные периферийные устройства виртуальной реальности
Современные периферийные устройства виртуальной реальности Компьютерные сети
Компьютерные сети Экспериментальное проектирование и процедура
Экспериментальное проектирование и процедура