Дискретные игры двух игроков с полной информацией. Тема 2.4.4

Человек с самого детства и всю жизнь играет в игры.
И если некоторое представление о детских, логических и компьютерных играх имеют все, то далеко не все знают, что, например, выбор банка, в котором следует открыть счет, — это тоже игра
Определимся сразу, что мы будем рассматривать не все игры, а только их определенный класс.
Нас будут интересовать игры с противоречивыми интересами сторон (антагонистические игры) и полной информацией об игре, и в первую очередь такая разновидность подобных игр, как игра двух лиц с нулевой суммой.

В рассматриваемых нами играх участвуют два игрока, которые ходят по очереди, причем оба они обладают полной информацией о текущей игровой ситуации (это определение исключает большинство карточных игр) и о возможных ходах очередного игрока. Игра считается оконченной, если достигнута позиция, являющаяся согласно правилам игры “терминальной” (конечной, заключительной), например, матовая позиция в шахматах. Правилами игры также устанавливается, каков исход игры в этой терминальной позиции.
Игра двух лиц (в дальнейшем будем называть их первый игрок и второй игрок, подразумевая игроков, которые ходят первым и вторым соответственно) с нулевой суммой означает, что выигрыш одного игрока является проигрышем другого (в ряде игр возможна ничья).

При этом в игре не должно быть бесконечных партий (бесконечных последовательностей позиций, в которых игроки ходят по правилам, но так и не попадают в заключительную позицию).
Чтобы задать конечную игру с полной информацией, нужно:
· указать конечное множество, элементы которого называются позициями игры;
· указать начальную позицию игры;
· указать множество заключительных позиций и задать результат игры в каждой из них;
· для каждой из остальных позиций указать возможные ходы, т.е. позиции, которые могут случиться после хода первого или второго игрока соответственно (в некоторых играх возможные ходы не зависят от того, какой именно игрок ходит).

Примерами рассматриваемых нами игр являются большинство настольных игр: шахматы, шашки, го, крестики-нолики, реверси и многие другие.
Если к тому же ни в каких аспектах игры (правилах, возможности или очередности ходов, определении момента завершения игры или результата) не участвует элемент случайности, такая игра будет еще и детерминированной.

Пусть в нашей игре не бывает “ничьих” и игроки ходят по очереди. Нетерминальная позиция называется выигрышной, если в ней существует какой-нибудь разрешенный ход, приводящий к выигрышу. С другой стороны, некоторая нетерминальная позиция является проигранной для игрока, если все разрешенные ходы из этой позиции ведут к позициям, в которых возможен выигрыш противника. Запишем это более формально.
Нетерминальная позиция x называется выигрышной для игрока, которому предоставлен ход, если существует хотя бы один ход, переводящий игру в проигрышную позицию. Нетерминальная позиция x называется проигрышной, если все ходы из позиции x ведут в выигрышные позиции.
Классификация позиций и стратегии игроков

Стратегией в конечной игре с полной информацией называется правило, указывающее, как следует игроку ходить в каждой из позиций, где ход за ним. Понятие стратегии не надо отождествлять с понятием хода.
Стратегия определяет полный план действий игрока при всевозможных ситуациях, могущих возникнуть в игре.
Стратегия называется выигрышной для игрока, если все партии, в которых он придерживается этой стратегии, заканчиваются выигрышем этого игрока.
Покажем, что в рассматриваемом нами классе игр обязательно существует выигрышная стратегия для одного из игроков, а все позиции игры можно разделить на выигрышные и проигрышные.
Классификация позиций и стратегии игроков

Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в два раза.
Например, имея кучу из 15 камней, за один ход можно получить кучу из 16 или 30 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится не менее 22.
Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 22 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 21.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока – значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.
Выполните следующие задания. Во всех случаях обосновывайте свой ответ.
Задача

Петя может выиграть за один ход.
При S≥22 игра завершается. Пети может:
добавить в кучу один камень (+1),
увеличить количество камней в куче в два раза (*2).
Рассмотрим каждый вариант:
(+1):S= 22−1=21
(*2): S=22\2=11 =>S∈[11;21]
11*2=22
12*2=24 (>22)
...
21*2=42 (>22)
Получим следующие стратегии:
при S∈[11;20] надо удвоить количество камней
при S=21 надо добавить один камень или удвоить количество камней
а) Укажите все такие значения числа S, при которых Петя может выиграть в один ход. Обоснуйте, что найдены все нужные значения S, и укажите выигрывающий ход для каждого указанного значения S.

Ваня может выиграть за один ход при любом ходе Пети.
Используем решение предыдущей задачи. Ваня может выиграть при S≥11. Но Ваня ходит 2-м, а Петя 1-м.
Нам нужно подобрать S.
11 можно получить следующим образом:
10+1
Построим дерево решений для S=10:
Получили, S=10.
Стратегия будет такой:
б) Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом. Опишите выигрышную стратегию Вани.

Петя не может выиграть 1-м ходом, он может выграть за 2 хода при любом ходе Вани:
Используем решение задачи части (б).
Дерево решений имеет вид:
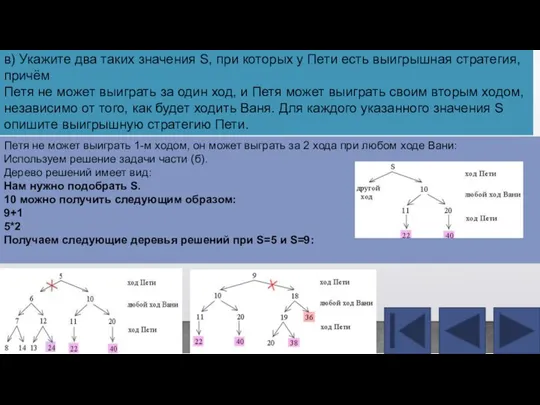
Нам нужно подобрать S.
10 можно получить следующим образом:
9+1
5*2
Получаем следующие деревья решений при S=5 и S=9:
в) Укажите два таких значения S, при которых у Пети есть выигрышная стратегия, причём
Петя не может выиграть за один ход, и Петя может выиграть своим вторым ходом, независимо от того, как будет ходить Ваня. Для каждого указанного значения S опишите выигрышную стратегию Пети.