Содержание
- 2. Логика – наука о законах мышления и его формах. Происходит от греческого слова логос – речь.
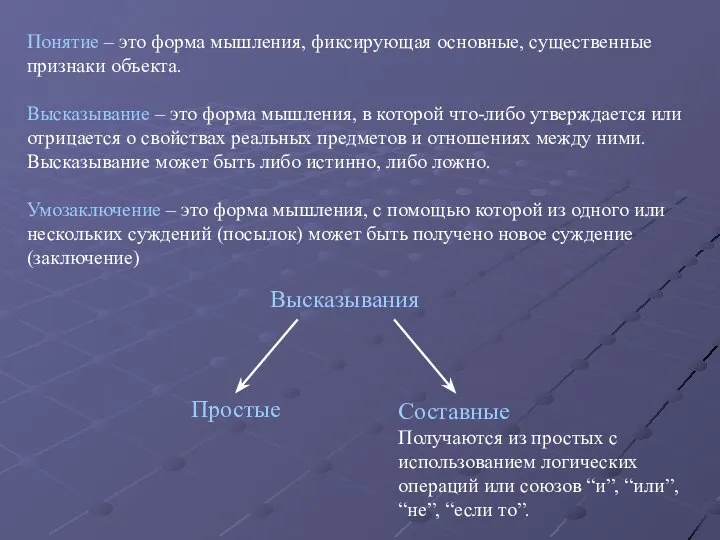
- 3. Понятие – это форма мышления, фиксирующая основные, существенные признаки объекта. Высказывание – это форма мышления, в
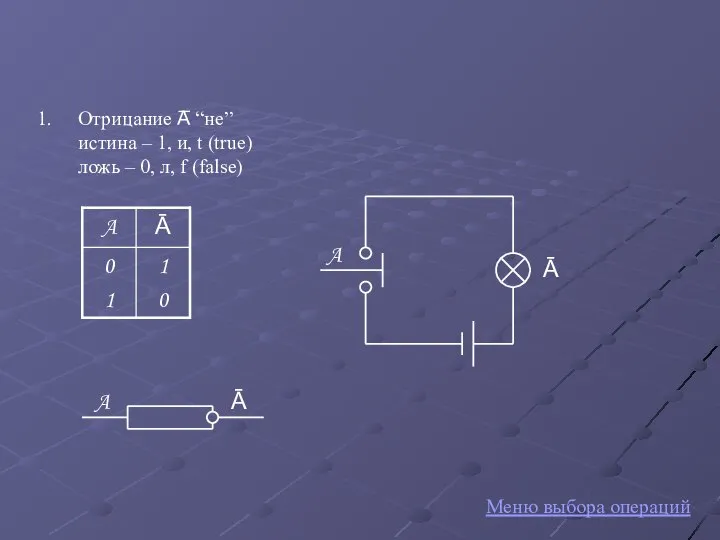
- 4. Простейшие логические операции Отрицание Конъюнкция Дизъюнкция Импликация Эквивалентность Штрих Шеффера Стрелка Пирса
- 5. Меню выбора операций
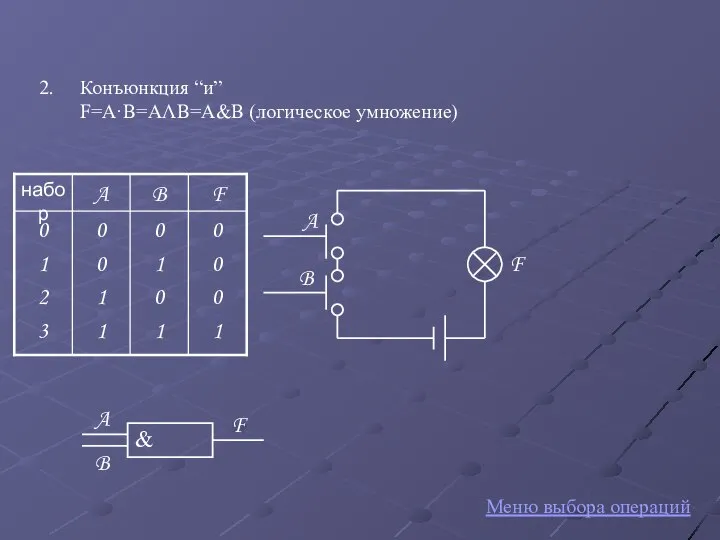
- 6. Конъюнкция “и” F=A·B=AΛB=A&B (логическое умножение) F A B Меню выбора операций
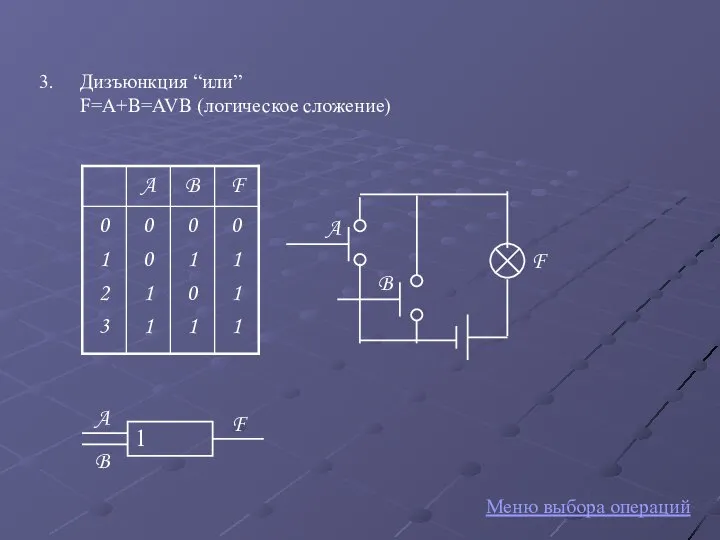
- 7. Дизъюнкция “или” F=A+B=AVB (логическое сложение) F A B Меню выбора операций
- 8. Импликация “если … то” F=A→B Импликация ложна тогда, когда предшествующее высказывание истинно, а последующее ложно. Меню
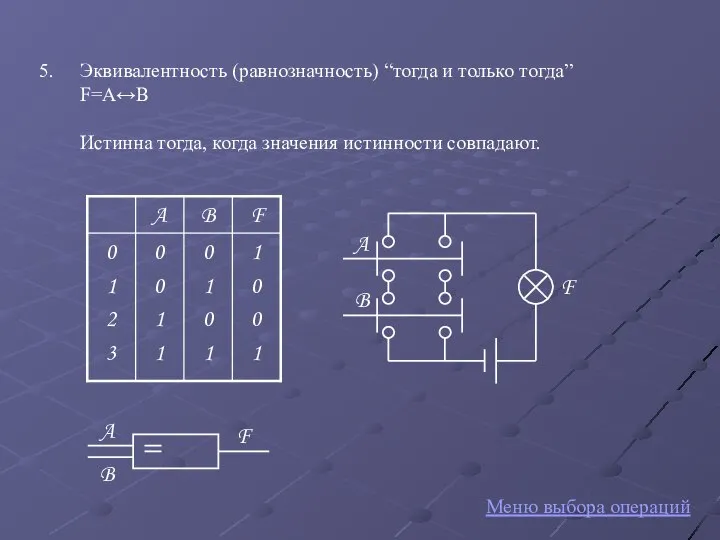
- 9. Эквивалентность (равнозначность) “тогда и только тогда” F=A↔B Истинна тогда, когда значения истинности совпадают. F A B
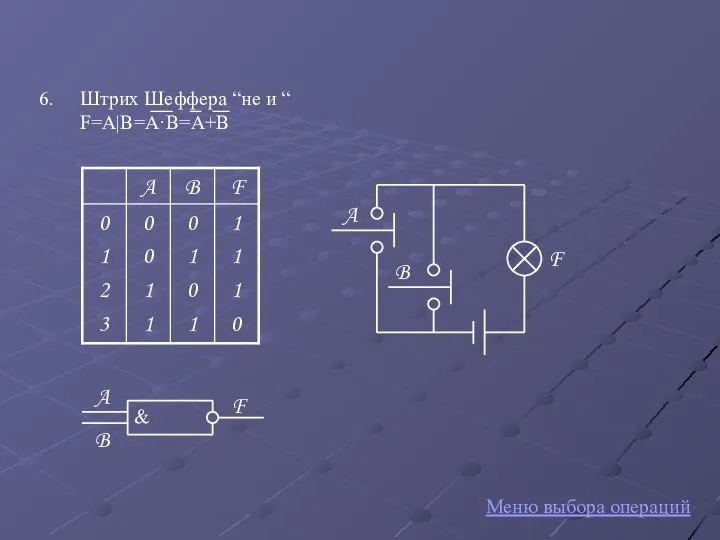
- 10. Меню выбора операций
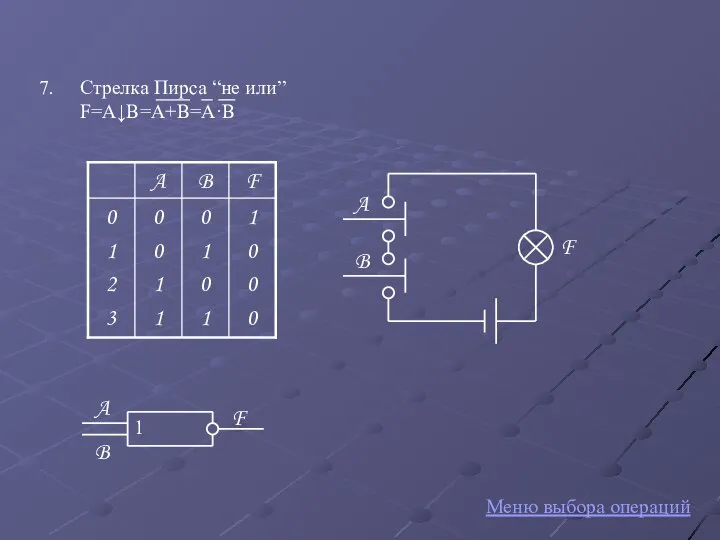
- 11. Меню выбора операций
- 12. Законы логики
- 13. Следствия из законов
- 14. Составление таблиц истинности по логическим формулам 1-ый способ 2-ой способ
- 15. Составление формул по заданным таблицам истинности Получение совершенно нормальной дизъюнктивной формы (СНДФ) Получение совершенной Получение совершенной
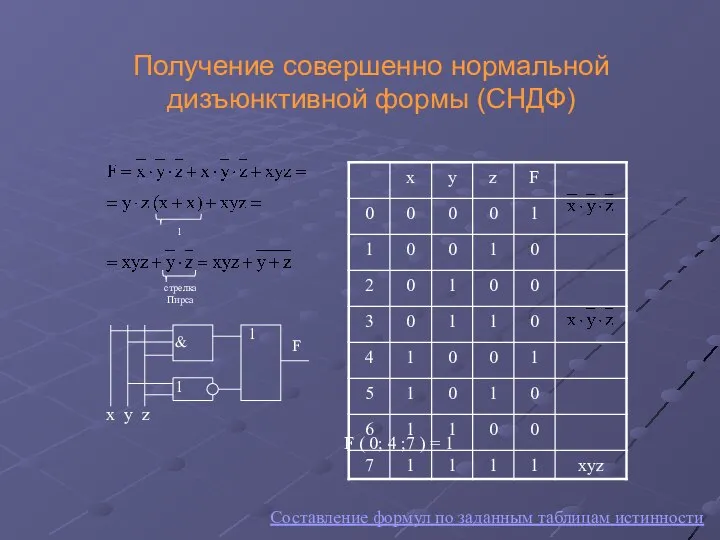
- 16. Получение совершенно нормальной дизъюнктивной формы (СНДФ) Составление формул по заданным таблицам истинности 1 стрелка Пирса F
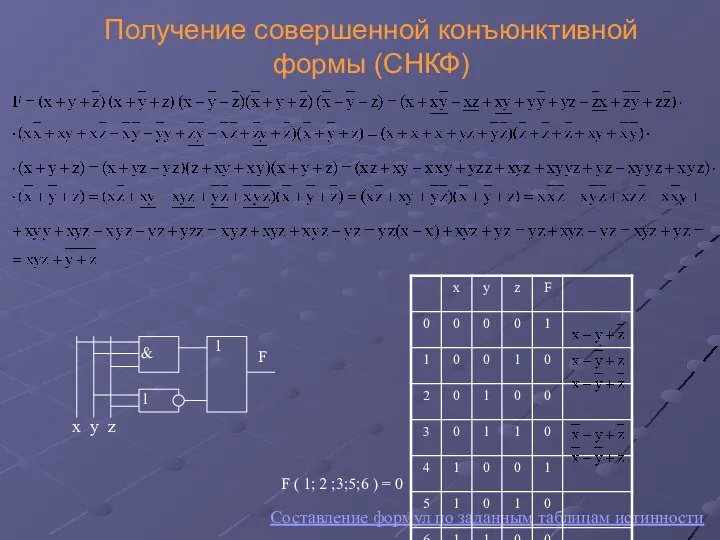
- 17. Получение совершенной конъюнктивной формы (СНКФ) Составление формул по заданным таблицам истинности F ( 1; 2 ;3;5;6
- 18. Схема одноразрядного сумматора
- 20. Скачать презентацию








 Алгоритмы и алгостихи
Алгоритмы и алгостихи Разработка сайта для привлечения молодежи к культуре тюркоязычного коренного народа
Разработка сайта для привлечения молодежи к культуре тюркоязычного коренного народа Презентация на тему Что такое программирование 9 класс
Презентация на тему Что такое программирование 9 класс  Роль материаловедения в графическом дизайне
Роль материаловедения в графическом дизайне Использование интернет-платформ в период дистанционного обучения
Использование интернет-платформ в период дистанционного обучения Мастерская записи и обработки звука Прямой эфир
Мастерская записи и обработки звука Прямой эфир Авторитарный протокол в сетевых боевиках
Авторитарный протокол в сетевых боевиках Статистическая обработка данных
Статистическая обработка данных Моделирование как метод познания
Моделирование как метод познания GET и POST запросы в MVC5
GET и POST запросы в MVC5 Вселенная коллекционера
Вселенная коллекционера Нанотехнологии в информатике
Нанотехнологии в информатике Федеральный мобильный гид по экообъектам, услугам и мероприятиям
Федеральный мобильный гид по экообъектам, услугам и мероприятиям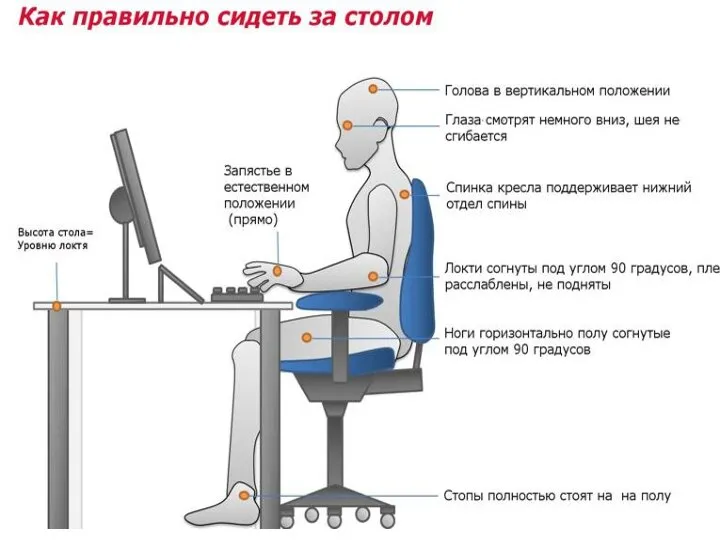 Как правильно сидеть за компьютером
Как правильно сидеть за компьютером Кооперация процессов и основные аспекты её логической организации
Кооперация процессов и основные аспекты её логической организации Привилегии баз данных
Привилегии баз данных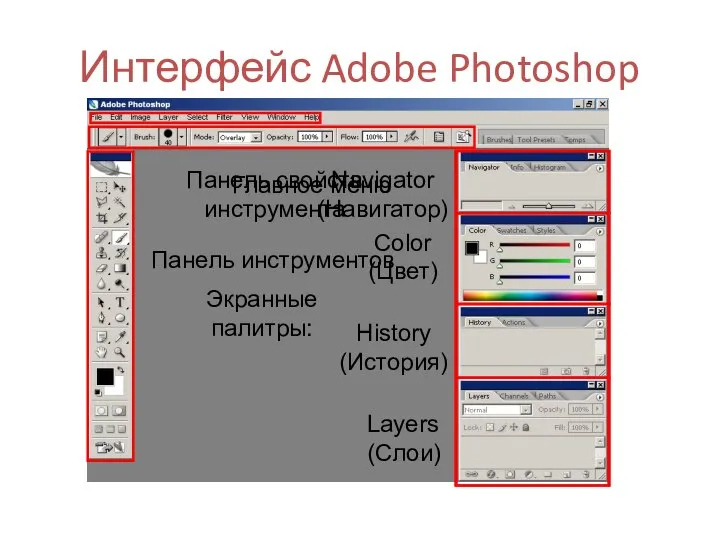 Интерфейс Adobe Photoshop
Интерфейс Adobe Photoshop Классификации ПО. Общие сведения
Классификации ПО. Общие сведения Внешние и внутренние компоненты ПК. Тема 13
Внешние и внутренние компоненты ПК. Тема 13 Курс Базы данных
Курс Базы данных Методы массивов. Метод массива splice
Методы массивов. Метод массива splice Введение в язык С
Введение в язык С Мониторинг деятельности классного коллектива средствами школьного СМИ
Мониторинг деятельности классного коллектива средствами школьного СМИ Debian. Выпуски Debian
Debian. Выпуски Debian Базіка - сервіс чат ботів
Базіка - сервіс чат ботів Двумерные массивы
Двумерные массивы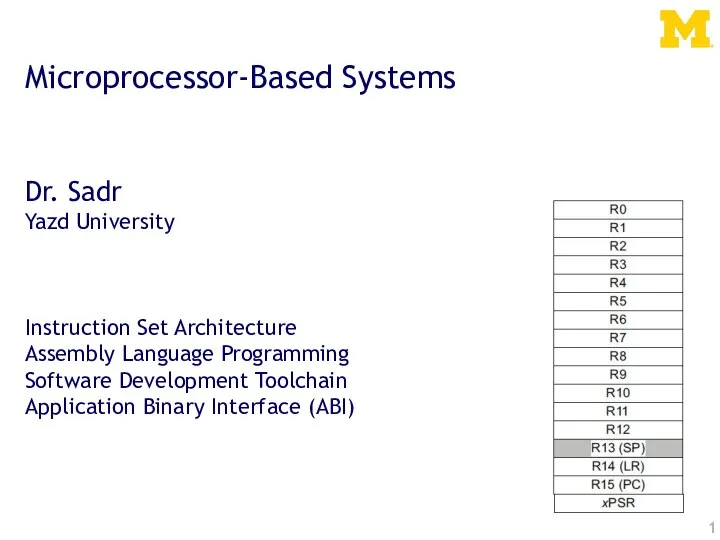 Microprocessor-Based Systems
Microprocessor-Based Systems Возможности текстового процессора WORD
Возможности текстового процессора WORD