формализующее элементарную теорию чисел. Наиболее популярная формализация основана на подходе Пеано, предложенном им в 1889 г. Язык этого исчисления кроме логических связок и равенства содержит нелогическую константу 0, двухместные функциональные символы +,⋅+,⋅, одноместный функциональный символ ′I′
Термы строятся из константы 0 и переменных с помощью функциональных символов; в частности, натуральные числа изображаются термами вида 0''^{\ldots}'0''^{\ldots}'
Атомарные формулы — это равенство термов; остальные формулы строятся из атомарных с помощью логических связок. В качестве аксиом выбираются логические аксиомы, это аксиомы формализованного исчисления предикатов и следующие нелогические (арифметические) формулы:
x=y→(x=z→y=z), ¬(x′=0);x=y→x′=y′,x′=y′→x=y;x+0=x,x+y′=(x+y)′;x⋅0=0,x⋅y′=(x⋅y)+x;(F(0)∧(∀x)(F(x)→F(x′)))→(∀x)(F(x)),x=y→(x=z→y=z), ¬(x′=0);x=y→x′=y′,x′=y′→x=y;x+0=x,x+y′=(x+y)′;x⋅0=0,x⋅y′=(x⋅y)+x;(F(0)∧(∀x)(F(x)→F(x′)))→(∀x)(F(x)),
где F(x)F(x) — произвольная формула теории с одной свободной предметной переменной xx
. Последняя формула есть схема аксиом, называемаясхемой аксиом индукции.
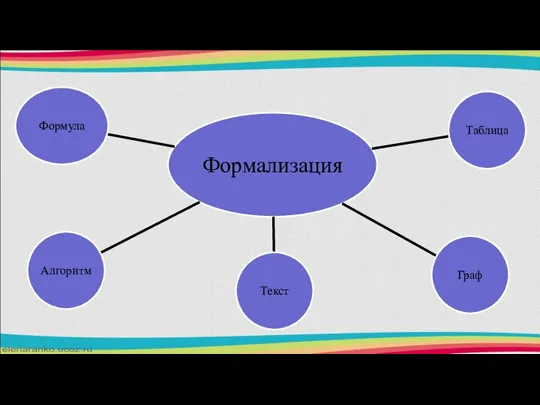
Формулы:
Терм — выражение формального языка (системы) специального вида. Понятие терма определяется индуктивно:
1, всякая индивидная константа есть терм;
2, всякая свободная переменная есть терм;











 Вход в Google Classroom Meet
Вход в Google Classroom Meet Модели жизненного цикла ПО. Жизненный цикл
Модели жизненного цикла ПО. Жизненный цикл Пакеты в Каталоге
Пакеты в Каталоге Операционная система Windows
Операционная система Windows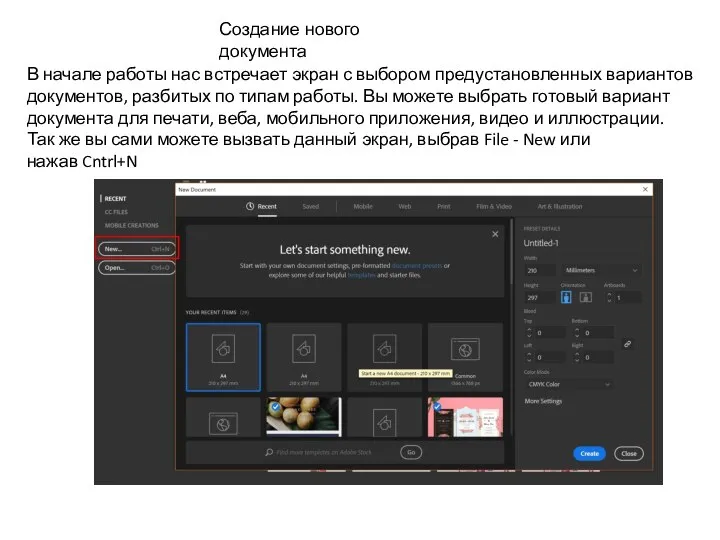 Создание нового документа
Создание нового документа Устройство компьютера
Устройство компьютера Идея приложения Flip
Идея приложения Flip неделя 1
неделя 1 Прикладной проект 3D-евятое царство
Прикладной проект 3D-евятое царство Продвижение библиотеки в социальных сетях
Продвижение библиотеки в социальных сетях Путешествуй. Блог
Путешествуй. Блог Журналистика
Журналистика Информатизация системы образования
Информатизация системы образования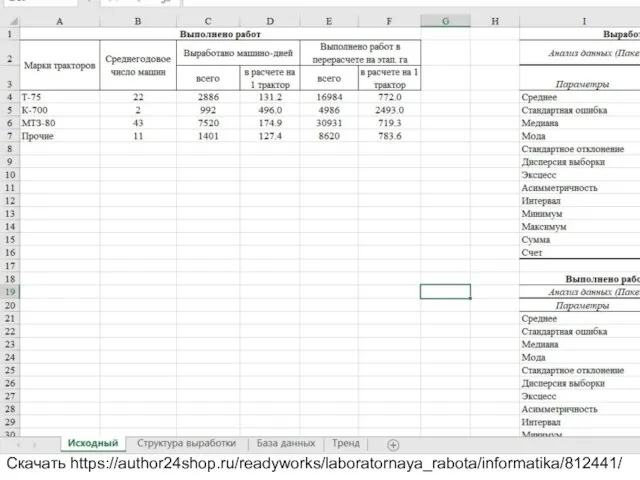 Вызвать Excel. Создать новую рабочую книгу
Вызвать Excel. Создать новую рабочую книгу Анимация. 8-9 класс
Анимация. 8-9 класс Информационные технологии тесты 1-13 (ответы)
Информационные технологии тесты 1-13 (ответы) Архитектура базы данных. Физическая и логическая независимость
Архитектура базы данных. Физическая и логическая независимость Одномерный массив
Одномерный массив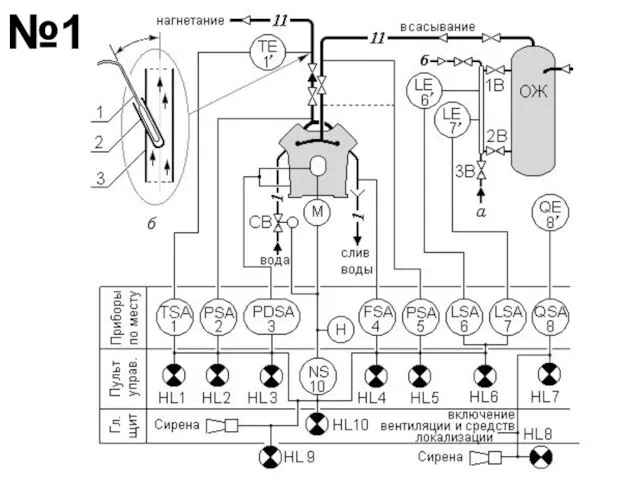 Системы автоматики
Системы автоматики Круглый стол. Цифровая 3D-медицина. Тенденции развития научно-исследовательской работы студентов Арзамасского филиала ННГУ
Круглый стол. Цифровая 3D-медицина. Тенденции развития научно-исследовательской работы студентов Арзамасского филиала ННГУ Ростейшие преобразования изображений
Ростейшие преобразования изображений Анализ соцсети
Анализ соцсети Игровой аркадный автомат
Игровой аркадный автомат Средства массовой информации (СМИ)
Средства массовой информации (СМИ) Безопасность в интернете
Безопасность в интернете 1666246426895__a84q6r
1666246426895__a84q6r Приклади застосування ГІС в аграрному секторі України
Приклади застосування ГІС в аграрному секторі України Создать БД Видеосалон
Создать БД Видеосалон