Геометрическое моделирование и компьютерная графика

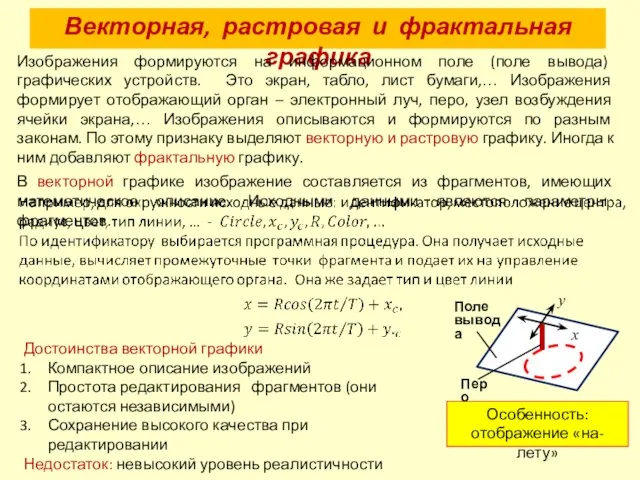
Векторная, растровая и фрактальная графика
Изображения формируются на информационном поле (поле вывода) графических устройств. Это экран, табло, лист бумаги,… Изображения формирует отображающий орган – электронный луч, перо, узел возбуждения ячейки экрана,… Изображения описываются и формируются по разным законам. По этому признаку выделяют векторную и растровую графику. Иногда к ним добавляют фрактальную графику.
В векторной графике изображение составляется из фрагментов, имеющих математическое описание. Исходными данными являются параметры фрагментов.
Достоинства векторной графики
Компактное описание изображений
Простота редактирования фрагментов (они остаются независимыми)
Сохранение высокого качества при редактировании
Недостаток: невысокий уровень реалистичности
Особенность: отображение «на-лету»

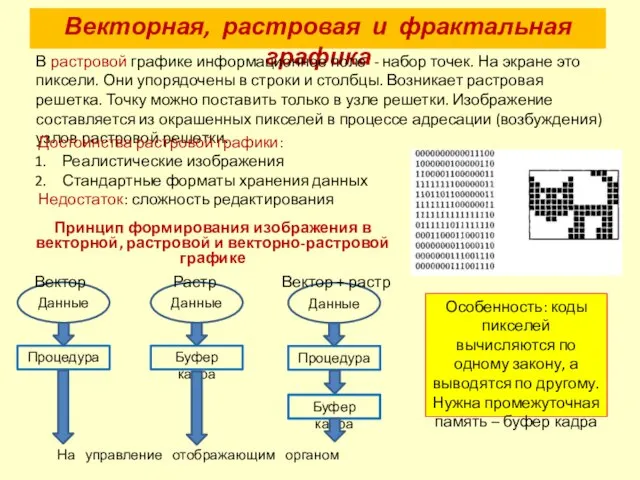
Векторная, растровая и фрактальная графика
В растровой графике информационное поле - набор точек. На экране это пиксели. Они упорядочены в строки и столбцы. Возникает растровая решетка. Точку можно поставить только в узле решетки. Изображение составляется из окрашенных пикселей в процессе адресации (возбуждения) узлов растровой решетки.
Особенность: коды пикселей вычисляются по одному закону, а выводятся по другому. Нужна промежуточная память – буфер кадра
Достоинства растровой графики:
Реалистические изображения
Стандартные форматы хранения данных
Недостаток: сложность редактирования

Векторная, растровая и фрактальная графика
Вычисления повторяются многократно, в идеале – до бесконечности, а реально – до достижения желаемого качества изображений. Это – отличительная особенность фрактальной графики.
В компьютерной графике фракталы используются для получения изображений узоров, текстур и геометрии природных объектов.
Снежинка Коха Папоротник Барнсли Метод смещения средней точки

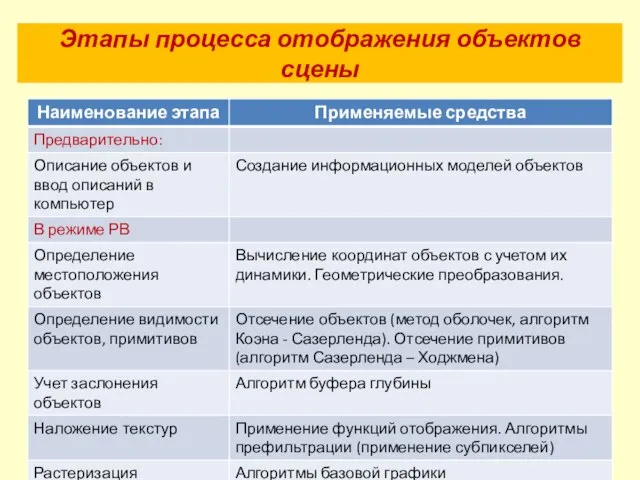
Этапы процесса отображения объектов сцены

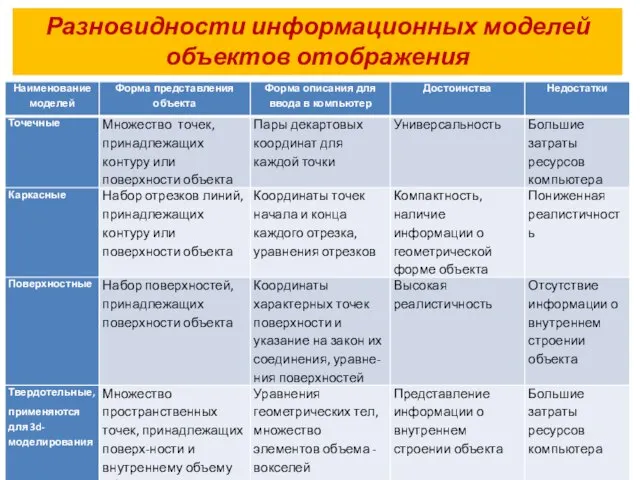
Разновидности информационных моделей объектов отображения

Иерархическая полигональная модель

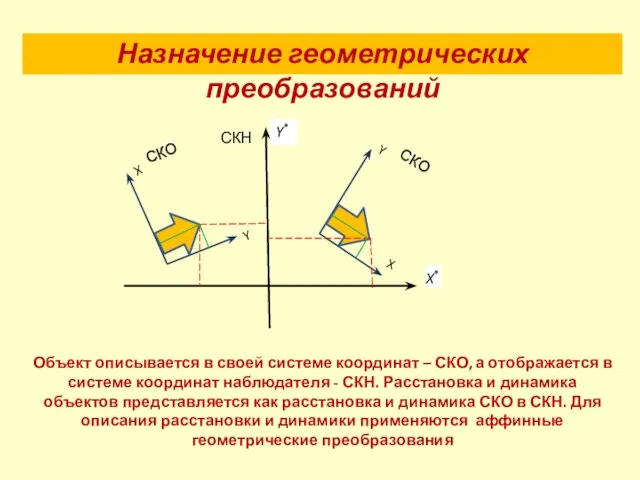
Объект описывается в своей системе координат – СКО, а отображается в системе координат наблюдателя - СКН. Расстановка и динамика объектов представляется как расстановка и динамика СКО в СКН. Для описания расстановки и динамики применяются аффинные геометрические преобразования
Назначение геометрических преобразований

Математическое описание аффинных преобразований
Общая форма координатного описания аффинных преобразований
x, y – координаты точки в «старой», а x*, y* – в «новой» системе координат, например в СКО и СКН
Частное преобразование поворота
ϕ – угол поворота СКО в СКН
Частное преобразование сдвига
x0*, y0* – координаты начала СКО в СКН
Частное преобразование масштабирования
k x , k y ≠ 0 – коэффициенты преобразования по координатным осям
Частное преобразование симметрии
α - угол наклона оси симметрии, проходящей через начало координат

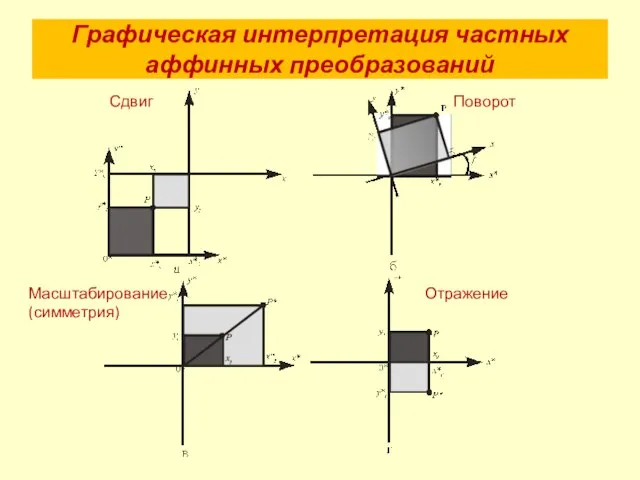
Графическая интерпретация частных аффинных преобразований
Сдвиг Поворот
Масштабирование Отражение (симметрия)

Немного о матрицах
При умножении на число каждый элемент матрицы умножается на это число

Перемножение матриц

Перемножение матриц
Учитывая правила перемножения, можно сформулировать признак возможности перемножения матриц: если одна матрица имеет размер А×В, а вторая – размер С×D, то для возможности перемножения нужно, чтобы В=С. Тогда результатом будет матрица размером А×D.
А×В С×D
Например, при перемножении матриц, имеющих размеры 5×3 и 3×4 получится матрица размера 5×4, матриц, имеющих размеры 1×3 и 3×3 – матрица размера 1×3, матриц, имеющих размеры 1×3 и 3×1 – матрица размера 1×1, т.е. просто число (скаляр).
В общем случае матрица S умножается на матрицу R по следующему правилу. Чтобы получить элемент результирующей матрицы, стоящий на пересечении i-ой строки и j-го столбца, нужно умножить i-ю строку S на j-й столбец R.
Должны быть одинаковыми
Размер результирующей матрицы

Однородные координаты
Однородным представлением n-мерного объекта в математике, в общем случае,
называют его представление в (n+1)-мерном пространстве, полученное добавлением
еще одной координаты – скалярного множителя. Однородные координаты на
плоскости определяются следующим образом.
Пусть на плоскости в аффинной системе координат задана точка P с координатами
(x, y). Однородными координатами этой точки называется любая тройка одновременно
не равных нулю чисел [w1 w2 w3], связанных с координатами точки P соотношениями:
Безразмерное число w3
называется скалярным
множителем.

Матричное описание аффинных преобразований в однородных координатах
Теперь аффинное преобразование в общем виде будет выглядеть следующим образом:
Перемножив матрицы, получим
Любое частное аффинное преобразование в матричной форме имеет вид
, где Т – матрица преобразования
Матрицы преобразований
сдвига поворота масштабирования отражения
Проверка
соответствия
для поворота

Суперпозиция матричных аффинных преобразований
A
A*
Использовав обозначения матриц, получим:
Произведение матриц, выделенное жирным, называется суперпозицией

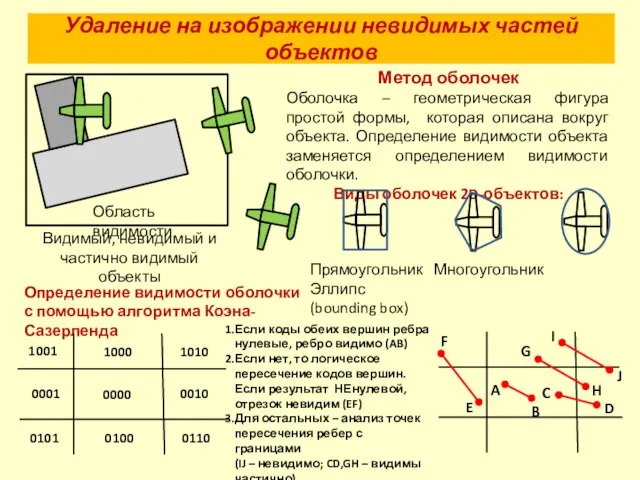
Удаление на изображении невидимых частей объектов
Метод оболочек
Оболочка – геометрическая фигура простой формы, которая описана вокруг объекта. Определение видимости объекта заменяется определением видимости оболочки.
Виды оболочек 2D-объектов:
Прямоугольник Многоугольник Эллипс
(bounding box)
Видимый, невидимый и частично видимый объекты
Определение видимости оболочки
с помощью алгоритма Коэна-Сазерленда
Если коды обеих вершин ребра нулевые, ребро видимо (AB)
Если нет, то логическое пересечение кодов вершин. Если результат НЕнулевой, отрезок невидим (EF)
Для остальных – анализ точек пересечения ребер с границами
(IJ – невидимо; CD,GH – видимы частично)

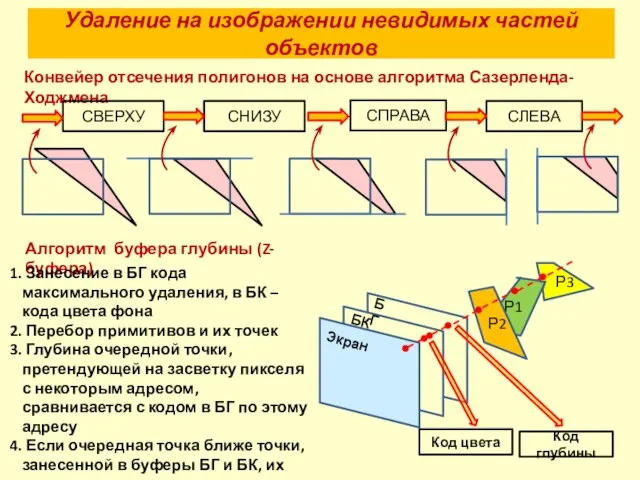
Удаление на изображении невидимых частей объектов
Конвейер отсечения полигонов на основе алгоритма Сазерленда-Ходжмена
Алгоритм буфера глубины (Z-буфера)
Занесение в БГ кода максимального удаления, в БК – кода цвета фона
Перебор примитивов и их точек
Глубина очередной точки, претендующей на засветку пикселя с некоторым адресом, сравнивается с кодом в БГ по этому адресу
Если очередная точка ближе точки, занесенной в буферы БГ и БК, их содержимое заменяется, иначе остается неизменным

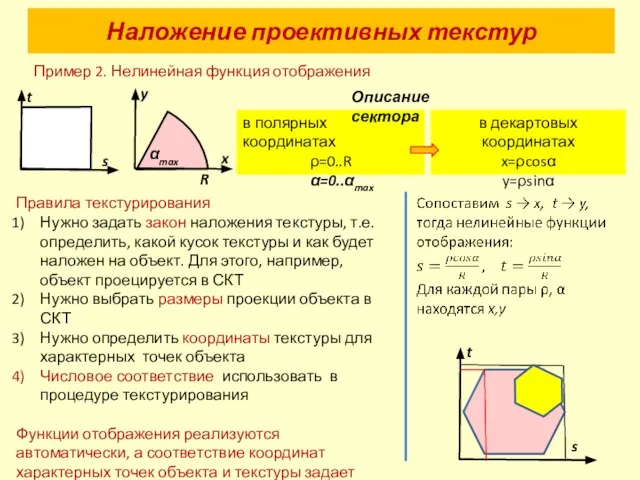
Наложение проективных текстур
Текстура – это характерный рисунок объекта, узор на его поверхности.
Текстура располагается в своей системе координат s,t (СКТ) и накладывается на объект, размещенный в его системе координат x,y (СКО).
Наложение текстуры (текстурирование) – это установление соответствия между элементами текстуры – текселями (texel) – и элементами растра – пикселями (pixel).
Другими словами, это установление соответствия между координатами s,t и координатами x,y, т.е. между координатами точек узора и координатами геометрии объекта. Описание такого соответствия – функция отображения: s=f(x,y), t=f(x,y).
Функции отображения бывают линейными и нелинейными
Пример 1. Линейная функция отображения
s
t
x
y
0.5
0.5
1
1
1
0
0
1
2
3
1
2
3
0=a·0+b·0+c c=0
0=d·0+e·0+f f=0
0.5=a·0+b·1+c b=0.5
1=d·0+e·1+f e=1
1=a·1+b·0+c a=1
0=d·1+e·0+f d=0
s=ax+by+c, s=x+0.5y,
t=dx+ey+f, t= y
Подставив в полученные выражения
координаты (x,y) любой точки объекта, найдем для нее s,t
Применение найденных коэффициентов дает искаженную текстуру.
А как не исказить?

Наложение проективных текстур
Пример 2. Нелинейная функция отображения
в декартовых координатах
x=ρcosα
y=ρsinα
в полярных координатах
ρ=0..R α=0..αmax
Описание сектора
Правила текстурирования
Нужно задать закон наложения текстуры, т.е. определить, какой кусок текстуры и как будет наложен на объект. Для этого, например, объект проецируется в СКТ
Нужно выбрать размеры проекции объекта в СКТ
Нужно определить координаты текстуры для характерных точек объекта
Числовое соответствие использовать в процедуре текстурирования
Функции отображения реализуются автоматически, а соответствие координат характерных точек объекта и текстуры задает разработчик

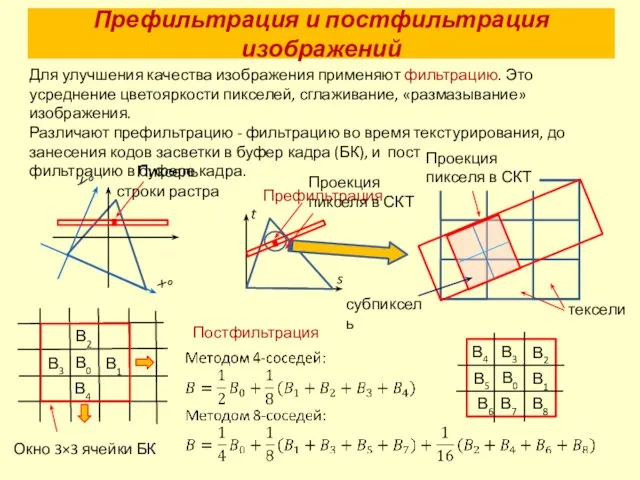
Префильтрация и постфильтрация изображений
Для улучшения качества изображения применяют фильтрацию. Это усреднение цветояркости пикселей, сглаживание, «размазывание» изображения.
Различают префильтрацию - фильтрацию во время текстурирования, до занесения кодов засветки в буфер кадра (БК), и постфильтрацию – фильтрацию в буфере кадра.
Префильтрация
Постфильтрация
Окно 3×3 ячейки БК
В2
В4
В6
В8

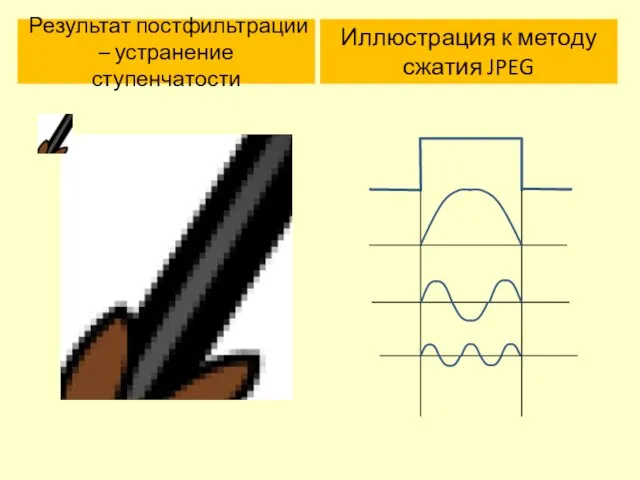
Результат постфильтрации – устранение ступенчатости
Иллюстрация к методу сжатия JPEG

Сжатие (компрессия) изображений и текстур
Сжатие изображений
Методы сжатия делятся на две группы: сжатие с потерями и сжатие без потерь (качества, информации). Первыми появились методы сжатия без потерь:
метод Хаффмана (Huffman), метод группового кодирования (run length encoding – RLE), метод Лемпеля – Зива - Уэлча (Lempel-Ziv-Welch – LZW).
Метод Хаффмана создан для сжатия текста, применяется в графике как вспомогательный. Для часто встречающихся в тексте символов используются короткие коды. Сжатие идет в 2 этапа: 1) анализ частоты повторения символов в сжимаемом тексте, составление таблицы кодирования; 2) замена символов текста их кодами из таблицы. Декомпрессия текста идет в обратном порядке. Коэффициент сжатия – до 8.
Метод RLE. Последовательность одинаковых по цветояркости пикселей заменяется двумя байтами: первый – количество одинаковых пикселей, второй – код цветояркости. Запись для изображения-примера: 4А2В3С. Коэффициент сжатия зависит от изображения и может достигать 32.
Запись изображения в память компьютера (в виде кодов цветояркости R-G-B) можно выполнять последовательно – пиксель за пикселем. Возникает цепочка троек кодов R-G-B. Это формат bmp. Буквенная запись показанного примера изображения:
AAAABBCCC. Сжатия нет. Объем памяти для хранения большой.
Сжатие изображений и текстур выполняется разными методами.

Сжатие (компрессия) изображений и текстур
Метод LZW. В строке изображения отыскиваются повторя-ющиеся фрагменты, расположение которых (адреса в строке) фиксируется в таблице. Исходное изображение заменяется кодами этих фрагментов и адресами их расположения. При декомпрессии фрагменты расставля-ются в строке по их адресам. Метод асимметричный. Коэффициент сжатия 5 – 7, но может достигать 100.
Позднее появился эффективный метод сжатия JPEG (Joint Photographic Experts Group).
Метод – с потерями, он отбрасывает в сигнале изображения до 50% информации о цвете (кодирует ее с меньшей разрядностью), а яркостный сигнал кодирует с большей разрядностью. Метод заменяет сходные оттенки цвета одним оттенком.
Метод JPEG реализуется по этапам
1. Переход от цветовой модели R-G-B к цветовой модели YUV (или - YCrCb).
2. Разбиение изображения на квадраты размером 8×8 пикселей.
3. Для каждого квадрата – переход от цветояркости пикселей к скорости (частоте) изменения цветояркости. Результат – числа, описывающие параметры частотных сигналов. Для этого применяется дискретное косинусное преобразование – ДКП. Компоненты с высокими частотами отбрасываются.
4. Полученные числа сжимаются методом RLE, а результат – еще методом Хаффмана.
При декомпрессии порядок действий обратный. Метод несимметричный. Коэффициент сжатия – до 100 и может задаваться.

Сжатие (компрессия) изображений и текстур
Метод сжатия текстур S3TC (Texture Compression фирмы S3)
Особенность работы с текстурами – произвольный доступ. Поэтому при сжатии текстуры разбиваются на фрагменты и сжимаются по этим фрагментам. При сжатии методом S3TC текстура разбивается на блоки размером 4×4 текселя.
10
10
10
10
01
01
01
01
01
00
00
00
00
00
В итоге, сжатый образ фрагмента – два 16-разрядных и шестнадцать 2-разрядных кодов, объем 64 бита. Образ без сжатия – шестнадцать 24-разрядных кодов, объем 384 бит. Коэффициент сжатия равен 6.
Декомпрессия выполняется схемными интерполяторами по приведенной формуле. Восстанавливаются не исходные цветояркости, а разрешенные уровни.
Метод S3TC – метод сжатия с потерями.

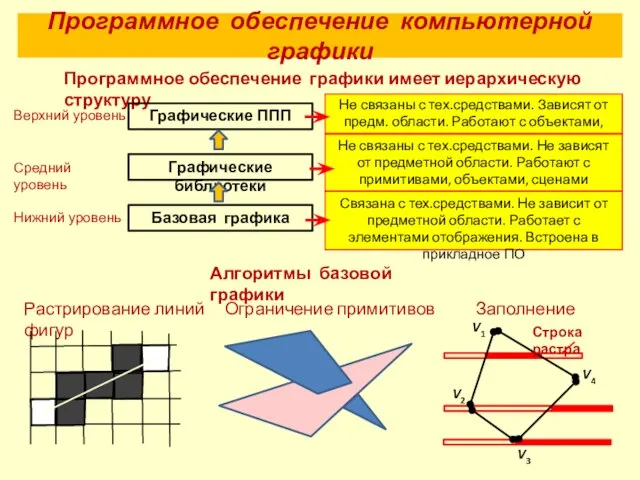
Программное обеспечение компьютерной графики
Программное обеспечение графики имеет иерархическую структуру
Не связаны с тех.средствами. Зависят от предм. области. Работают с объектами, сценами
Не связаны с тех.средствами. Не зависят от предметной области. Работают с примитивами, объектами, сценами
Связана с тех.средствами. Не зависит от предметной области. Работает с элементами отображения. Встроена в прикладное ПО
Верхний уровень
Средний уровень
Нижний уровень
Алгоритмы базовой графики
Растрирование линий Ограничение примитивов Заполнение фигур
V1
V2
V3
V4
Строка растра

Программное обеспечение компьютерной графики
Графические библиотеки (на примере OpenGL)
Причины появления: повторение процедур построения часто встречающихся графических объектов в различных программах. Около 20 лет назад появилось полтора десятка библиотек. Сейчас по факту – три: OpenGL, DirectX, Vulkan.
Содержание: это набор макропроцедур – команд. Они выполняют конкретные графические операции, параметры которых настраиваются.
Возможности: создание 2d- и 3d-объектов произвольной формы в виде точечных, «проволочных» и поверхностных моделей; генерация стандартных трехмерных поверхностей (сфера, куб, цилиндр и др.); моделирование освещения 3d-объектов; цветная закраска и наложение текстур; задание шести степеней свободы и масштабирования объектов; улучшение качества изображения с помощью пирамиды текстур, отбраковки нелицевых примитивов, теста глубины, фильтрации, эффектов.
Структура: базовый набор команд (более 300) и несколько расширений (glu, glaux, glut, wgl,…). Группы команд отвечают за геометрию, динамику, закраску и текстурирование, материалы и освещение объектов, пиксельные операции, сценарные преобразования, режим отображения, анализ выполнения команд.
Геометрические примитивы: точки, прямые линии, плоские многоугольники. Есть укрупненные примитивы: поверхности 2-го порядка, многогранники, чайник Юта.
Недостатки: нет команд для обращения к периферийным устройствам.

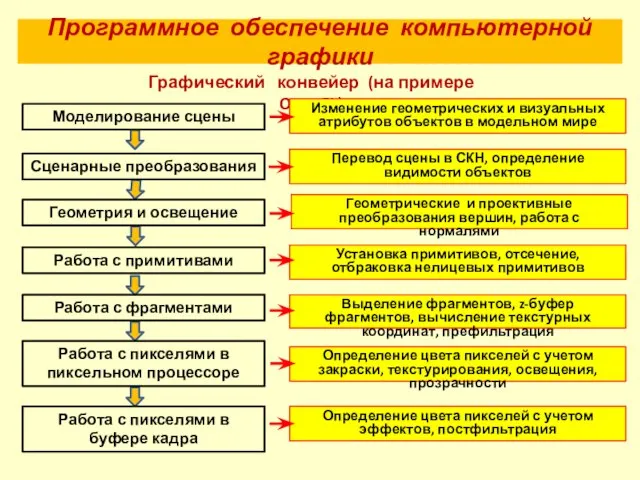
Графический конвейер (на примере OpenGL)
Программное обеспечение компьютерной графики