Слайд 2Определение
Предок (в наиболее используемом понимании), родитель – это вершина, из которой был

совершён переход в данную.
Предок вершины в дереве – любая вершина, расположенная на пути от данной до корня.
Наименьший общий предок двух вершин – это вершина максимально удалённая от корня дерева, которая является предком для обоих этих вершин.
Слайд 3Алгоритм поиска циклов
Проведём поиск в глубину. Если граф ненаправленный, то дополнительно для

каждой вершины будем хранить родителя (номер вершины, из которой мы пришли в текущую), переход в родителя осуществлять не будем.
Если в какой-то момент обхода мы зашли в серую вершину, то мы нашли цикл.
С момента нахождения цикла будем добавлять текущую вершину в перечень вершин цикла и откатываться к предыдущей, пока не дойдём то старта цикла.
Слайд 4Разница в нахождении цикла в направленном и ненаправленном графах
1
2
Нет цикла
1
2
Нет цикла
1
2
Есть цикл

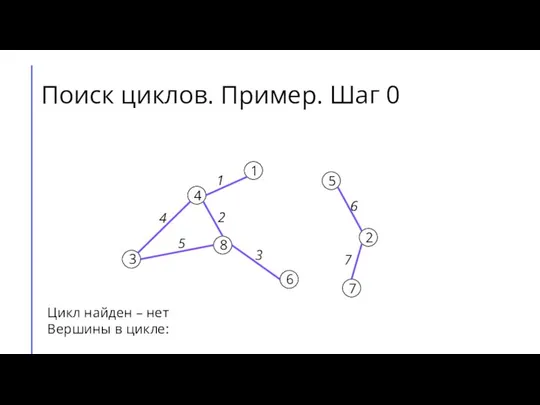
Слайд 5Поиск циклов. Пример. Шаг 0
7
2
6
5
8
3
4
1
1
3
2
5
4
6
7
Цикл найден – нет
Вершины в цикле:
Слайд 67
2
6
5
8
3
4
1
1
3
2
6
7
5
4
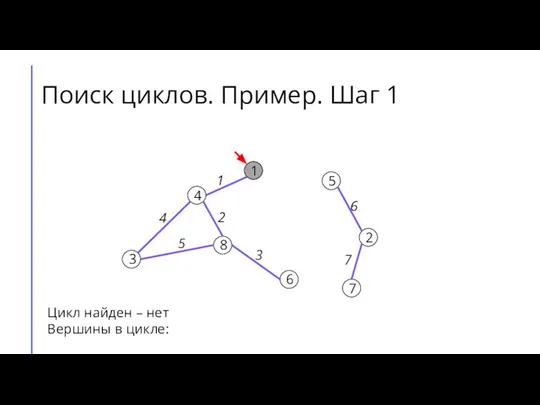
Цикл найден – нет
Вершины в цикле:
Поиск циклов. Пример. Шаг 1
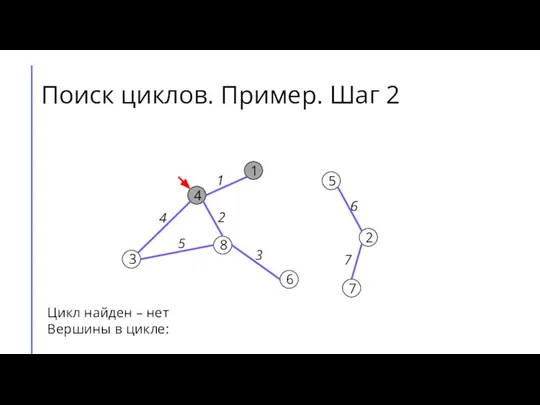
Слайд 7Поиск циклов. Пример. Шаг 2
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4
Цикл найден – нет
Вершины в цикле:
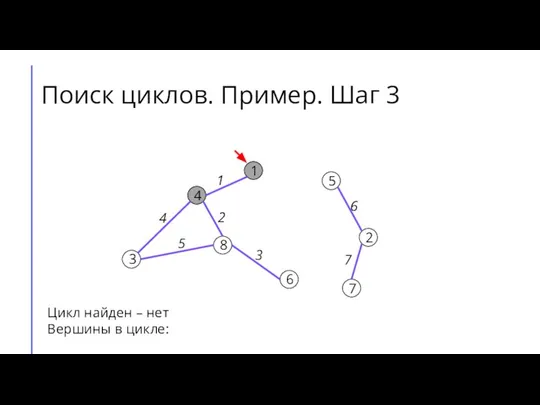
Слайд 8Поиск циклов. Пример. Шаг 3
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4
Цикл найден – нет
Вершины в цикле:
Слайд 9Поиск циклов. Пример. Шаг 4
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4
Цикл найден – нет
Вершины в цикле:
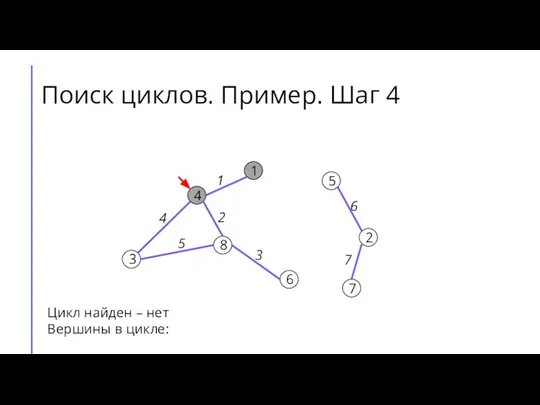
Слайд 10Поиск циклов. Пример. Шаг 5
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4
Цикл найден – нет
Вершины в цикле:
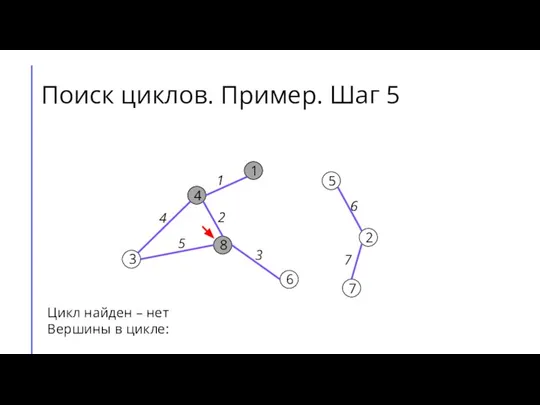
Слайд 11Поиск циклов. Пример. Шаг 6
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4
Цикл найден – нет
Вершины в цикле:
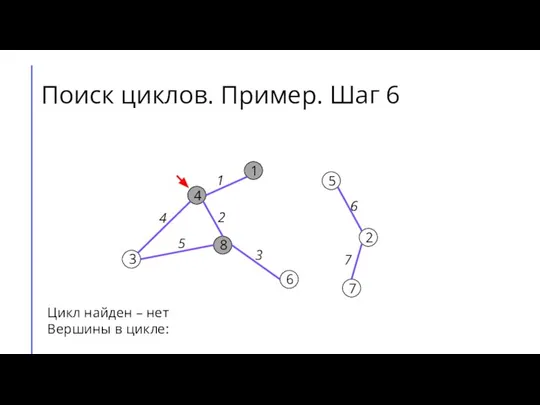
Слайд 12Поиск циклов. Пример. Шаг 7
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4
Цикл найден – нет
Вершины в цикле:
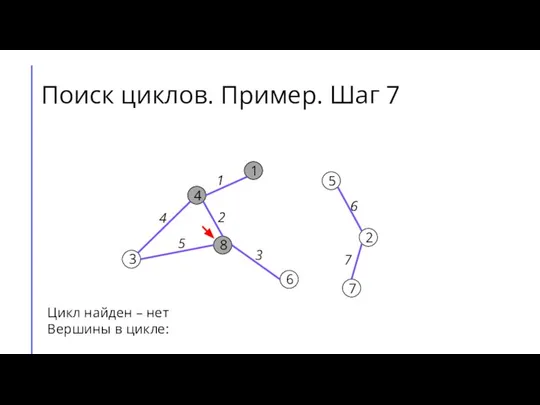
Слайд 13Поиск циклов. Пример. Шаг 8
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4
Цикл найден – нет
Вершины в цикле:
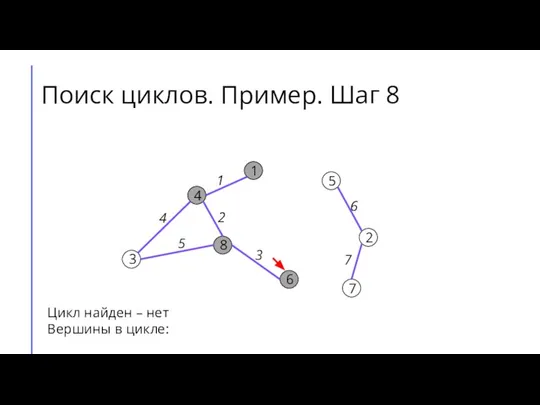
Слайд 14Поиск циклов. Пример. Шаг 9
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4
Цикл найден – нет
Вершины в цикле:
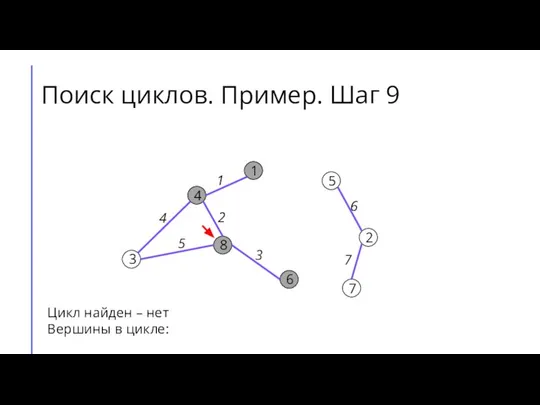
Слайд 15Поиск циклов. Пример. Шаг 10
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4
Цикл найден – нет
Вершины в цикле:
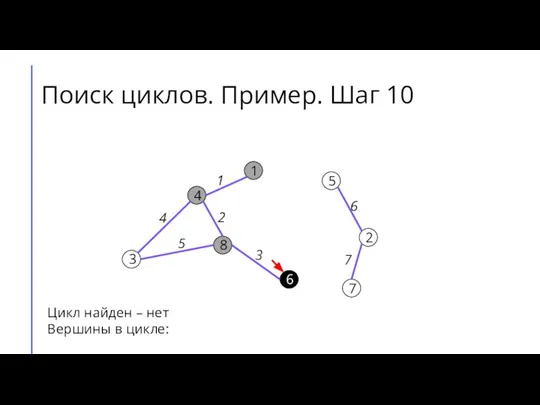
Слайд 16Поиск циклов. Пример. Шаг 11
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4
Цикл найден – нет
Вершины в цикле:
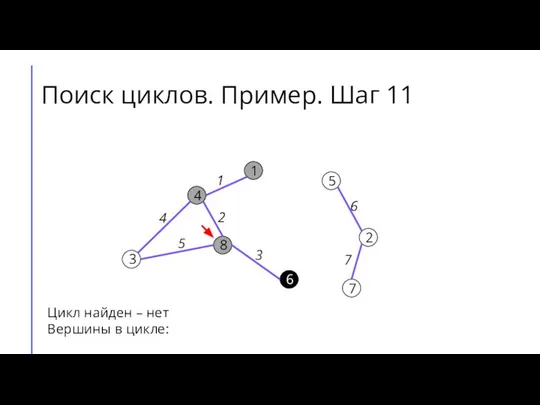
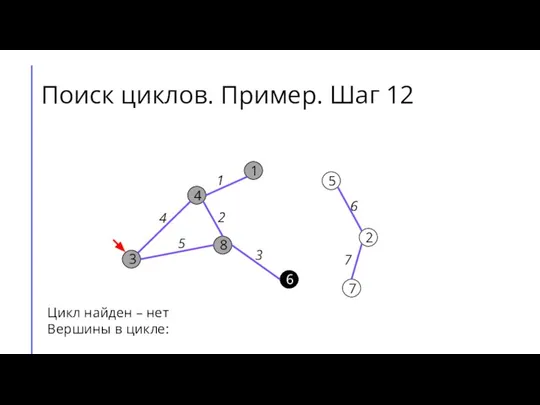
Слайд 17Поиск циклов. Пример. Шаг 12
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4
Цикл найден – нет
Вершины в цикле:
Слайд 18Поиск циклов. Пример. Шаг 13
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4
Цикл найден – да
Вершины в цикле: 4

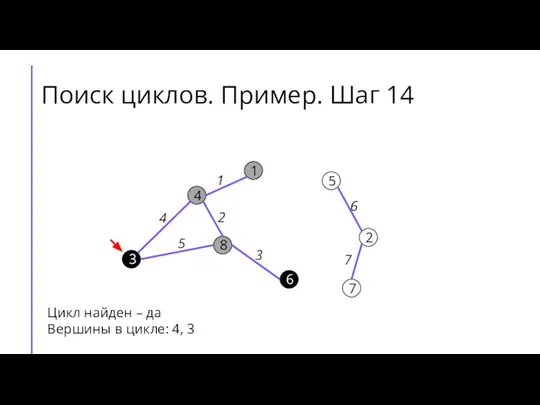
Слайд 19Поиск циклов. Пример. Шаг 14
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4
Цикл найден – да
Вершины в цикле: 4, 3
Слайд 20Поиск циклов. Пример. Шаг 15
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4
Цикл найден – да
Вершины в цикле: 4, 3,
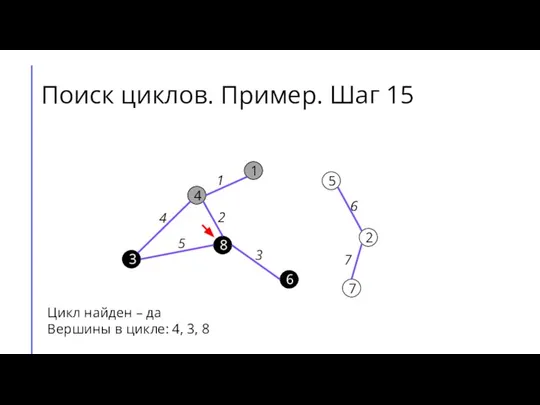
8
Слайд 21Поиск циклов. Пример. Шаг 16
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4
Цикл найден – да
Вершины в цикле: 4, 3,
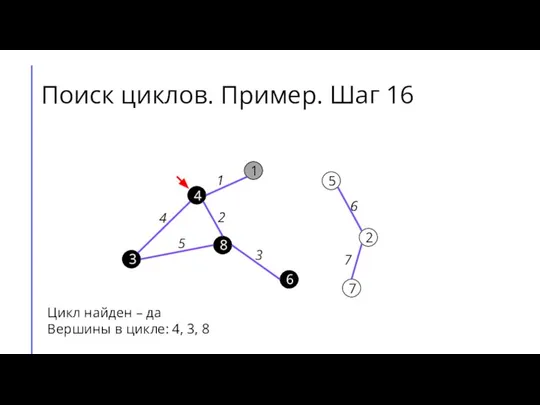
8
Слайд 22Поиск циклов. Пример. Шаг 17
7
2
6
5
8
3
4
1
1
3
2
6
7
5
4
Цикл найден – да
Вершины в цикле: 4, 3,
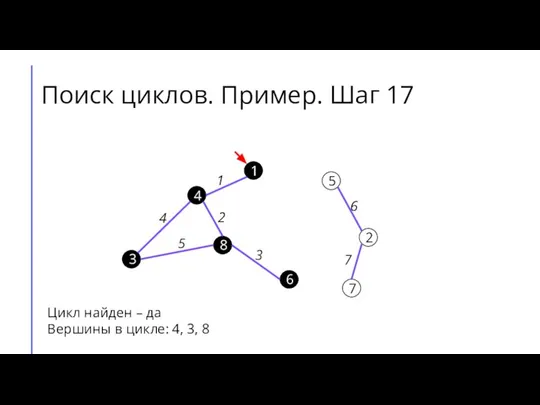
8
Слайд 23Реализация
На рисунке представлен алгоритм нахождения цикла в ненаправленном графе.
В цикле в функции

main вызов поиска осуществляется как dfs(i, -1), а не dfs(i).
Для направленного графа не нужно обрабатывать случай с предком.
Слайд 24Алгоритм проверки является ли одна вершина предком для другой
Для каждой вершины будем

дополнительно хранить время входа в неё (tin) и время выхода (tout).
Для этого заведём глобальный таймер. При входе в вершину запомним значение таймера в tin, и увеличим таймер на 1. Аналогично при выходе из вершины.
Вершина А является предком вершины В тогда и только тогда, когда A.tin ≤ B.tin и B.tout ≤ A.tout.
Стоит отметить, что при такой формулировке каждая вершина является своим же предком. Если такое явление нежелательно, то неравенства следует заменить на строгие.
Слайд 25Предки в дереве
0
1
2
3
5
6
4
8
7
9
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
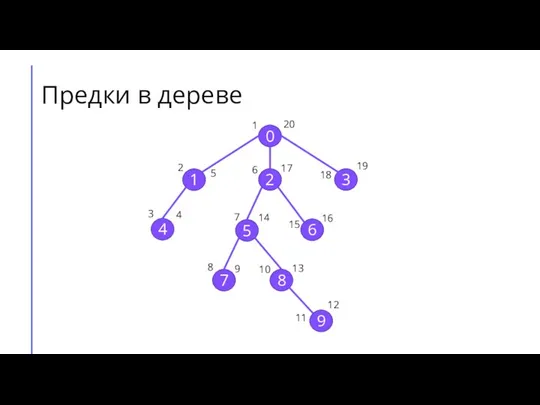
Слайд 26Наивный алгоритм нахождения наименьшего общего предка вершин А и В
С помощью обхода

в глубину, запущенного из корня, для каждой вершины посчитаем её время входа, время выхода и глубину (удалённость от корня).
В качестве результата на старте алгоритма возьмём корень дерева.
Переберём все вершины. Если вершина является предком для обеих вершин А и В, и она расположена глубже, чем текущая вершина, хранящаяся в результате, то данная вершина становится новым результатом.

























 Библиотека Кировских островов
Библиотека Кировских островов Итераторы и функциональные объекты
Итераторы и функциональные объекты Основы программирования (на языке Си). Массивы
Основы программирования (на языке Си). Массивы Проект Витрина
Проект Витрина Шаблоны писем
Шаблоны писем Профессия гейм-дизайнер
Профессия гейм-дизайнер Урок - игра Основы информатики
Урок - игра Основы информатики Мировой класс лидирующих компаний в цифровой струйной печати
Мировой класс лидирующих компаний в цифровой струйной печати Архитектура современной ЭВМ. Состав и характеристики комплектующих современного персонального компьютера
Архитектура современной ЭВМ. Состав и характеристики комплектующих современного персонального компьютера Skype-конференция
Skype-конференция 3. Выбор жизненного цикла ИТ-проекта.Использование гибких подходов в управлении ИТ-проектами
3. Выбор жизненного цикла ИТ-проекта.Использование гибких подходов в управлении ИТ-проектами Примеры использования внешних устройств. Программное обеспечение внешних устройств
Примеры использования внешних устройств. Программное обеспечение внешних устройств Создание комплексной системы обеспечения информационной безопасности инфраструктуры Росреестра
Создание комплексной системы обеспечения информационной безопасности инфраструктуры Росреестра Хранители Равновесия
Хранители Равновесия База данных
База данных Технические новинки первой мировой войны
Технические новинки первой мировой войны Структуры данных: стеки, деки, очереди
Структуры данных: стеки, деки, очереди Интерактивная доска (ИД)
Интерактивная доска (ИД) Презентация на тему Примеры моделирования
Презентация на тему Примеры моделирования  Информационные технологии. Тема № 3. Основы защиты информации
Информационные технологии. Тема № 3. Основы защиты информации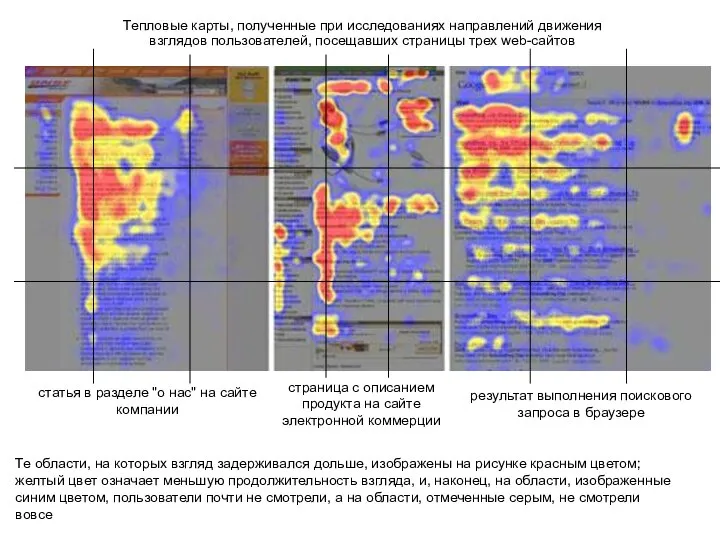 Тепловые карты, полученные при исследованиях направлений движения взглядов пользователей, посещавших страницы трех web-сайтов
Тепловые карты, полученные при исследованиях направлений движения взглядов пользователей, посещавших страницы трех web-сайтов Функциональное программное обеспечение решения управленческих задач
Функциональное программное обеспечение решения управленческих задач Дизайн и графика. Web-страницы
Дизайн и графика. Web-страницы Источники пространственных данных. Их типы. Способы получения данных
Источники пространственных данных. Их типы. Способы получения данных Организация сетевого администрирования
Организация сетевого администрирования 3
3 One Drive
One Drive Создание групп (сообществ) в образовательной сети
Создание групп (сообществ) в образовательной сети