Содержание
- 2. Для представления вещественных чисел (конечных и бесконечных десятичных дробей) используют формат с плавающей точкой (запятой). Форма
- 3. Например, число 25,324 можно записать в таком виде: 0.25324х102. Здесь m=0.25324 — мантисса, n=2 — порядок.
- 4. Получается, что представление числа в форме с плавающей точкой неоднозначно? Чтобы не было неоднозначности, в ЭВМ
- 5. Иначе говоря, мантисса меньше единицы и первая значащая цифра — не ноль. Значит для рассмотренного числа
- 6. Пусть в памяти компьютера вещественное число представляется в форме с плавающей точкой в двоичной системе счисления
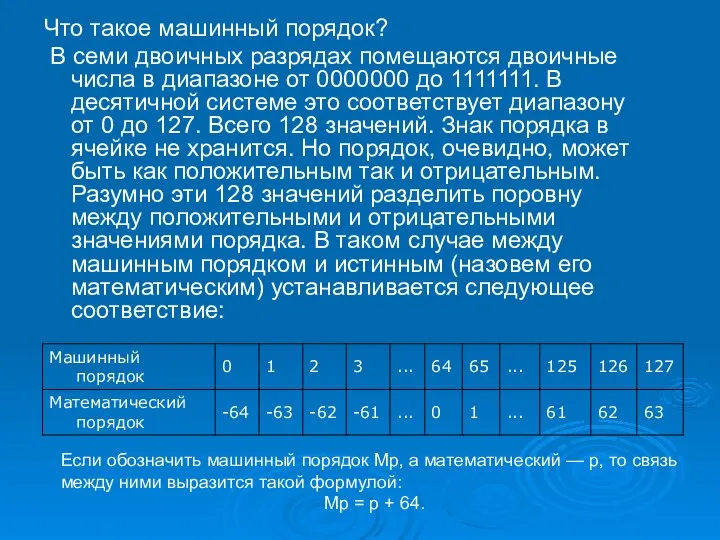
- 7. Что такое машинный порядок? В семи двоичных разрядах помещаются двоичные числа в диапазоне от 0000000 до
- 8. Итак, машинный порядок смещён относительно математического на 64 единицы и имеет только положительные значения. При выполнении
- 9. Теперь мы можем записать внутреннее представление числа 25,324 в форме с плавающей точкой. 1)Переведем его в
- 10. Число в форме с плавающей точкой занимает в памяти компьютера 4 байта (число обычной точности) или
- 11. Для того, чтобы получить внутреннее представление отрицательного числа -25,324, достаточно в полученном выше коде заменить в
- 12. Задание. Представьте двоичное число -100,12 в четырёхбайтовом формате. Представьте число сначала в форме с плавающей запятой.
- 14. Скачать презентацию










 21-1
21-1 Пути изучения английского языка с помощью глобальной сети интернет
Пути изучения английского языка с помощью глобальной сети интернет Социальные сети: история создания
Социальные сети: история создания Презентация+Изучаем+интерфейс+соцсетей.+Технические+аспекты+работы
Презентация+Изучаем+интерфейс+соцсетей.+Технические+аспекты+работы Программа Photomath
Программа Photomath Полиграфический дизайн текст и изображение
Полиграфический дизайн текст и изображение Развивающая игра Прочитай по первым буқвам. Часть 1 Слова из 3-х букв
Развивающая игра Прочитай по первым буқвам. Часть 1 Слова из 3-х букв Путеводитель по политическим философам
Путеводитель по политическим философам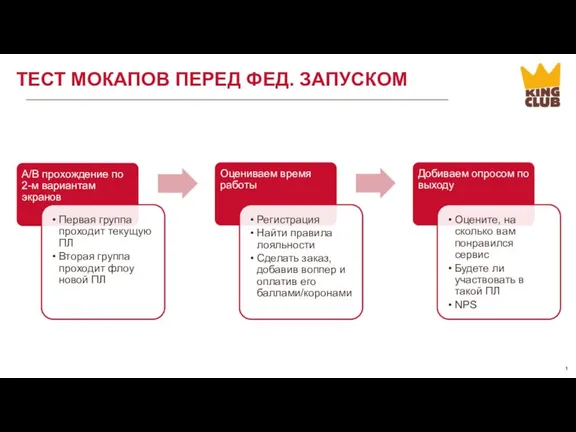 Тест ФЛОУ Мокапов перед фед. запуском
Тест ФЛОУ Мокапов перед фед. запуском Текст и графика
Текст и графика Адаптивная верстка
Адаптивная верстка Погрузись в мир анимации powerpoint
Погрузись в мир анимации powerpoint Интернет-мошенничество
Интернет-мошенничество Новые технологии в Русском музее Санкт-Петербурга
Новые технологии в Русском музее Санкт-Петербурга Работа с программным обеспечением. Инсталляция программного обеспечения
Работа с программным обеспечением. Инсталляция программного обеспечения Центр автоматизации энергосбережения
Центр автоматизации энергосбережения Media Qualification
Media Qualification Создание web-сайта
Создание web-сайта Тайны кроссворда
Тайны кроссворда Организационные процессы жизненного цикла программного средства
Организационные процессы жизненного цикла программного средства Поиск информации в Интернете
Поиск информации в Интернете Чек-листы и тест-кейсы
Чек-листы и тест-кейсы Создание веб-страниц в Word
Создание веб-страниц в Word 9-1-5
9-1-5 Как продвигать свои проекты ВКонтакте
Как продвигать свои проекты ВКонтакте Компьютерные сети интернет
Компьютерные сети интернет Презентация на защиту проекта
Презентация на защиту проекта Безопасный интернет
Безопасный интернет