задачи за конечное число действий, при любом наборе исходных данных.» Википедия
Требования к алгоритму:
Конечность(результативность) алгоритма означает, что за конечное число шагов должен быть получен результат;
Дискретность алгоритма означает, что алгоритм должен быть разбит на последовательность выполняемых шагов;
Понятность алгоритма означает, что алгоритм должен содержать только те команды, которые входят в набор команд, который может выполнить конкретный исполнитель;
Точность алгоритма означает, что каждая команда должна пониматься однозначно;
Массовость алгоритма означает, что однажды составленный алгоритм должен для решения подобных задач с разными исходными данными;
Детерминированность (определенность). Алгоритм обладает свойством детерминированности, если для одних и тех же наборов исходных данных он будет выдавать один и тот же результат, т.е. результат однозначно определяется исходными данными.










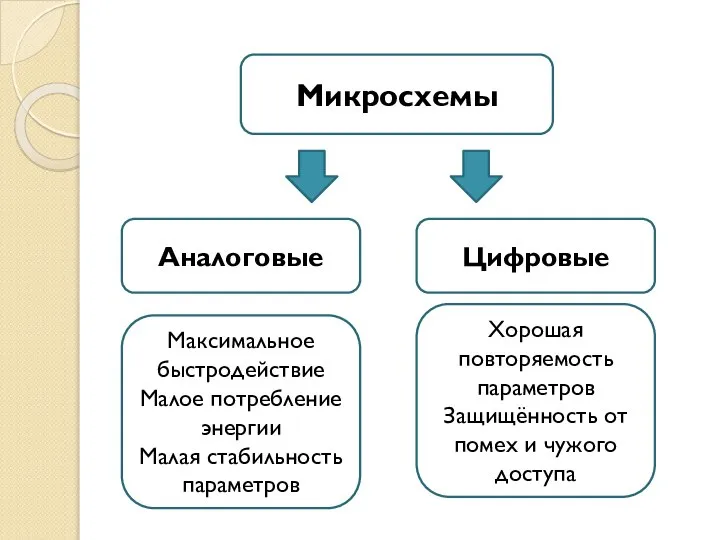 Аналоговые, цифровые микросхемы
Аналоговые, цифровые микросхемы Портфолио Войтович Анны
Портфолио Войтович Анны Основные функции современной системы офисной автоматизации. Занятие №2
Основные функции современной системы офисной автоматизации. Занятие №2 Информационная система новостного контента
Информационная система новостного контента Автоматизация и обеспечение информационной безопасности процесса ведения документации и отчетности в ИП Ким С.Г
Автоматизация и обеспечение информационной безопасности процесса ведения документации и отчетности в ИП Ким С.Г Системы счисления
Системы счисления Информационно-аналитическая деятельность как объект технологической поддержки
Информационно-аналитическая деятельность как объект технологической поддержки Системное ПО. Работа с файлами
Системное ПО. Работа с файлами Проверка закономерностей методом рассуждений. Тренировочный тест для подготовки к ЕГЭ по информатике
Проверка закономерностей методом рассуждений. Тренировочный тест для подготовки к ЕГЭ по информатике Стилистические особенности пресс-релиза
Стилистические особенности пресс-релиза Как считать скорость
Как считать скорость Тайны шифрования
Тайны шифрования Программирование циклических алгоритмов. Лекция 3
Программирование циклических алгоритмов. Лекция 3 Scratch Middle. Случайные числа
Scratch Middle. Случайные числа Реляционное исчисление кортежей. Система запросов
Реляционное исчисление кортежей. Система запросов Okna_i_operatsii_nad_oknami
Okna_i_operatsii_nad_oknami Как можно представить информацию?
Как можно представить информацию? Летающий Автомобиль
Летающий Автомобиль Морской фон
Морской фон Технические средства информационных технологий
Технические средства информационных технологий Ferma — аренда облачных касс для бизнеса
Ferma — аренда облачных касс для бизнеса Презентация таблицы обезличенных ID сети Вконтакте
Презентация таблицы обезличенных ID сети Вконтакте Программирование разветвляющихся алгоритмов
Программирование разветвляющихся алгоритмов Разработка ИСБ склада ГСМ технической зоны аэропорта 2-го класса
Разработка ИСБ склада ГСМ технической зоны аэропорта 2-го класса Dependency Injection. Неявное управление зависимостями
Dependency Injection. Неявное управление зависимостями Язык Python. Начало
Язык Python. Начало От персонального компьютера к персональному производству
От персонального компьютера к персональному производству Тренировки по видеосвязи
Тренировки по видеосвязи