Содержание
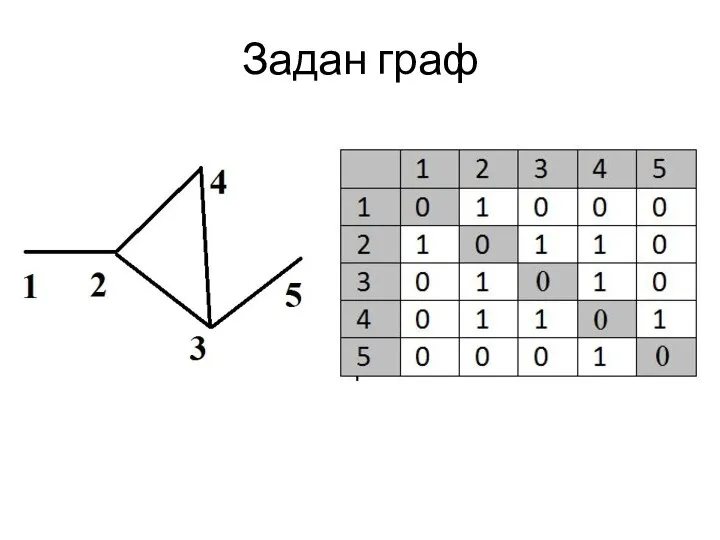
- 2. Задан граф
- 3. Ввод данных int main() { int G[100][100], // граф транспортной сети R[100][100], // минимальные расстояния //
- 4. Oпределение длины кратчайших путей int r[100]={0}, // 0 – расстояние не определено ob[100], // обработанные вершины
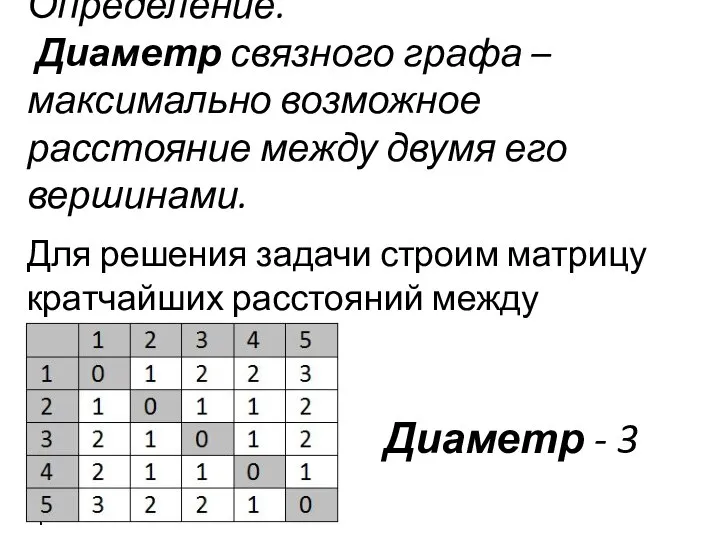
- 5. Определение. Диаметр связного графа – максимально возможное расстояние между двумя его вершинами. Для решения задачи строим
- 6. Определение диаметра графа int D=0; For(i=1; i For(i=1; i D:= max(D,R[i][j]); Cout
- 7. Определение. Радиус связного графа – максимально возможное расстояние между двумя его вершинами. Для решения задачи строим
- 8. Определение радиуса графа int Rad=0; for(i=1; i int M=0; for(i=1; i M:= max(M,R[i][j]); if (i==1) Rad=M;
- 9. Определение. Центр графа – вершина, максимальное расстояние от которого до любой другой вершины является наименьшим из
- 11. Скачать презентацию
![Ввод данных int main() { int G[100][100], // граф транспортной сети R[100][100],](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1111046/slide-2.jpg)
![Oпределение длины кратчайших путей int r[100]={0}, // 0 – расстояние не определено](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1111046/slide-3.jpg)
![Определение диаметра графа int D=0; For(i=1; i For(i=1; i D:= max(D,R[i][j]); Cout](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1111046/slide-5.jpg)



 Skype-конференция
Skype-конференция Разработка Web-сайтов с использованием языка разметки гипертекста HTML
Разработка Web-сайтов с использованием языка разметки гипертекста HTML Блоги и блогеры
Блоги и блогеры Занятие № 2 Основы программирования на C#
Занятие № 2 Основы программирования на C# История развития электронновычислительной техники
История развития электронновычислительной техники Анонимность в интернете
Анонимность в интернете Бесплатный курс по созданию авторского видео на компьютере для начинающих пользователей
Бесплатный курс по созданию авторского видео на компьютере для начинающих пользователей История развития вычислительной техники
История развития вычислительной техники Оформление библиографического описания
Оформление библиографического описания Побудова мережі доступу на основі технології WiMAX для сільської місцевості
Побудова мережі доступу на основі технології WiMAX для сільської місцевості Информационно-библиотечный центр
Информационно-библиотечный центр Автоматизированная информационная система Автосервис
Автоматизированная информационная система Автосервис Безопасность, гигиена, эргономика, защита информации
Безопасность, гигиена, эргономика, защита информации Урок 3. Уникальность. Как отстроиться от конкурентов
Урок 3. Уникальность. Как отстроиться от конкурентов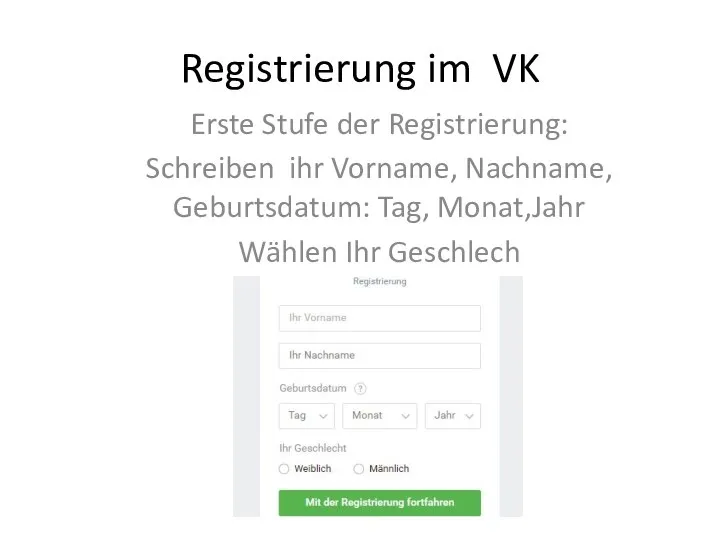 Registrierung im VK
Registrierung im VK Поняття бази даних
Поняття бази даних Программирование. Выпускной проект
Программирование. Выпускной проект Цифровой след
Цифровой след Контрольная работа. Общие принципы построения ЭВМ
Контрольная работа. Общие принципы построения ЭВМ NET Framework – программная платформа
NET Framework – программная платформа Интерфейс Sound Forge 9.0 (часть 2)
Интерфейс Sound Forge 9.0 (часть 2) Математика в программировании
Математика в программировании Датчики положения и перемещения в робототехнике (ДПП). Основные понятия и определения
Датчики положения и перемещения в робототехнике (ДПП). Основные понятия и определения Виды компьютерной графики
Виды компьютерной графики Вася на Сене
Вася на Сене Технологии Ethernet, Fast Ethernet,Token Ring и Gigabit Ethernet
Технологии Ethernet, Fast Ethernet,Token Ring и Gigabit Ethernet Порты ввода-вывода
Порты ввода-вывода Цель ведения аккаунта
Цель ведения аккаунта