Содержание
- 2. Алгоритм RSA Основные сведения Алгоритм шифрования с открытым ключом RSA был предложен одним из первых в
- 3. Алгоритм RSA Криптографическая система RSA базируется на следующих двух фактах из теории чисел: задача проверки числа
- 4. Шифрование Итак, рассмотрим сам алгоритм. Пусть абонент А хочет передать зашифрованное сообщение абоненту Б. В этом
- 5. Шифрование Затем случайным образом выбирается число d Далее необходимо найти число е, такое, что еd mod
- 6. Шифрование Так как пользователь Б хочет получить зашифрованное сообщение от пользователя А, значит пользователь Б должен
- 7. Шифрование Второй этап – шифрование данных. Если абонент А хочет передать некоторые данные абоненту Б, он
- 8. Шифрование Абонент Б, получивший зашифрованное сообщение, расшифровывает все блоки полученного сообщения по формуле Все расшифрованные блоки
- 9. Пример вычислений по алгоритму Пусть пользователь А хочет передать пользователю Б сообщение. В этом случае вначале
- 10. Пример вычислений по алгоритму Пусть d = 13. Это число будет одним из компонентов открытого ключа.
- 11. Пример вычислений по алгоритму Теперь пользователь Б должен запомнить свой закрытый ключ 17, отправить открытый ключ
- 12. m1 = 1717 mod 33 = 8 m2 = 1517 mod 33 = 27 m3 =
- 13. Вопросы практического использования алгоритма RSA На протяжении многих лет алгоритм RSA активно используется как в виде
- 14. Вопросы практического использования алгоритма RSA Для обеспечения высокой надежности шифрования необходимо, чтобы выступающее в качестве модуля
- 15. Вопросы практического использования алгоритма RSA Сами авторы RSA рекомендовали использовать следующие размеры модуля N: 768 бит
- 16. Вопросы практического использования алгоритма RSA С размером ключей связан и другой аспект реализации RSA - вычислительный.
- 17. Вопросы практического использования алгоритма RSA При этом как шифрование, так и расшифрование включают возведение большого целого
- 18. Вопросы практического использования алгоритма RSA Алгоритм RSA реализуется как программным, так и аппаратным путем. Многие мировые
- 19. Вопросы практического использования алгоритма RSA Алгоритм RSA может использоваться для формирования электронной цифровой подписи, а также
- 20. Вопросы для проверки Для каких целей может применяться алгоритм RSA? Опишите процесс шифрования с использованием алгоритма
- 21. Упражнения для проверки Пусть пользователь А хочет передать пользователю Б сообщение m=10, зашифрованное с помощью алгоритма
- 22. Алгоритм Диффи-Хеллмана Первая публикация данного алгоритма появилась в 70-х годах ХХ века в статье Диффи и
- 23. Алгоритм Диффи-Хеллмана Алгоритм основан на трудности вычислений дискретных логарифмов. Попробуем разобраться, что это такое. В этом
- 24. Алгоритм Диффи-Хеллмана Причем, имея Х, вычислить Y легко. Обратная задача вычисления X из Y является достаточно
- 25. Формирование общего ключа Пусть два пользователя, которых условно назовем пользователь 1 и пользователь 2, желают сформировать
- 26. Формирование общего ключа Затем первый пользователь выбирает число Х1 (X1 которое он посылает второму абоненту. Аналогично
- 27. Формирование общего ключа После этого у пользователей должна быть информация, указанная в следующей таблице: Из чисел
- 28. Формирование общего ключа Никто другой кроме пользователя 1 этого сделать не может, так как число Х1
- 29. Формирование общего ключа Безопасность формирования общего ключа в алгоритме Диффи-Хеллмана вытекает из того факта, что, хотя
- 30. Пример вычислений по алгоритму Пусть два абонента, желающие обмениваться через Интернет зашифрованными сообщениями, решили сформировать секретный
- 31. Пример вычислений по алгоритму Затем пользователи обмениваются открытыми ключами Y1 и Y2. После этого каждый из
- 32. Вопросы практического использования алгоритма Диффи-Хеллмана Для того, чтобы алгоритм Диффи-Хеллмана работал правильно, то есть оба пользователя,
- 33. Вопросы практического использования алгоритма Диффи-Хеллмана Только в этом случае для любого целого Y Y = AХmod
- 34. Тогда в качестве А можно взять любое число, для которого справедливы неравенства 1 На подбор подходящих
- 35. Вопросы практического использования алгоритма Диффи-Хеллмана Следует заметить, что данный алгоритм, как и все алгоритмы асимметричного шифрования,
- 36. Вопросы для проверки Для каких целей может применяться алгоритм Диффи-Хеллмана? Опишите последовательность действий при использовании алгоритма
- 37. Упражнения для проверки Вычислите закрытые ключи Y1, Y2 и общий ключ Z для системы Диффи-Хеллмана с
- 38. Алгоритм Эль-Гамаля Асимметричный алгоритм, предложенный в 1985 году Эль-Гамалем (T. ElGamal), универсален. Он может быть использован
- 39. Алгоритм Эль-Гамаля И в случае шифрования, и в случае формирования цифровой подписи каждому пользователю необходимо сгенерировать
- 40. Алгоритм Эль-Гамаля Затем каждый абонент группы выбирает свое секретное число Хi, 1 Таким образом, каждый пользователь
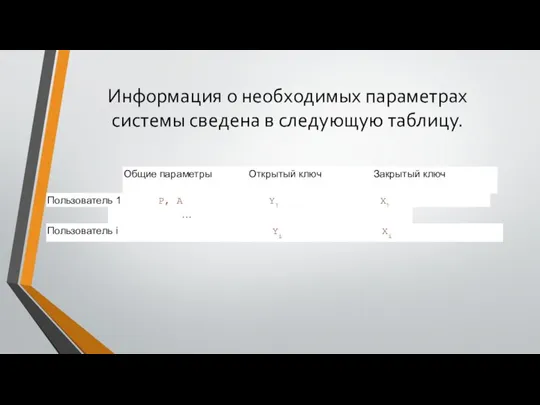
- 41. Информация о необходимых параметрах системы сведена в следующую таблицу.
- 42. Шифрование Теперь рассмотрим, каким образом производится шифрование данных. Сообщение, предназначенное для шифрования, должно быть представлено в
- 43. Шифрование Пара чисел (r, е), являющаяся шифротекстом, передается второму пользователю. Второй пользователь, получив (r,e), для расшифрования
- 44. Шифрование Если злоумышленник узнает или перехватит Р, А, Y2, r, e, то он не сможет по
- 45. Шифрование По аналогичному алгоритму может производиться и согласование ключа, используемого для симметричного шифрования больших объемов данных.
- 46. Пример шифрования Пусть два абонента, обменивающиеся через Интернет зашифрованными сообщениями, имеют следующие общие параметры: Р =
- 47. Пример шифрования Первый абонент выбирает случайно число k, например k = 7. Число k должно быть
- 48. Вопросы для проверки Для каких целей может применяться алгоритм Эль-Гамаля?. Опишите последовательность действий при использовании алгоритма
- 49. Упражнения для проверки В системе связи, применяющей шифр Эль-Гамаля, пользователь 1 желает передать сообщение m пользователю
- 51. Скачать презентацию















































 Вся наша жизнь – в Internet
Вся наша жизнь – в Internet Области применения вычислительных систем (шкала условная, логарифмическая)
Области применения вычислительных систем (шкала условная, логарифмическая) Объединение компьютеров в локальную сеть. Организация работы пользователей в локальных компьютерных сетях
Объединение компьютеров в локальную сеть. Организация работы пользователей в локальных компьютерных сетях Мотивация оператора. Договор присоединения
Мотивация оператора. Договор присоединения Презентация на тему Форматирование текста в MS Word
Презентация на тему Форматирование текста в MS Word  Мифы о медийных личностях
Мифы о медийных личностях Майнкрафт
Майнкрафт Язык программирования Java
Язык программирования Java Программно-управляемая система нанесения графической информации на вертикальные поверхности
Программно-управляемая система нанесения графической информации на вертикальные поверхности Разнообразие исполнителей алгоритмов. Основы алгоритмизации
Разнообразие исполнителей алгоритмов. Основы алгоритмизации Как продвигаться юристу в Instagram
Как продвигаться юристу в Instagram Основы формальной теории защиты информации
Основы формальной теории защиты информации Компьютерная арифметика. Хранение в памяти целых чисел
Компьютерная арифметика. Хранение в памяти целых чисел Введение в Processing
Введение в Processing Сортировки. Внутренние сортировки (1)
Сортировки. Внутренние сортировки (1) Отчёт-презентация. Прохождение практики ОАО НПО Квант
Отчёт-презентация. Прохождение практики ОАО НПО Квант Основные модели предоставления услуг облачных вычислений: Software as a Service (SaaS) (ПО как услуга)
Основные модели предоставления услуг облачных вычислений: Software as a Service (SaaS) (ПО как услуга) Графический редактор PAINT
Графический редактор PAINT Весна идет!
Весна идет! Программно-аппаратная защита (Лекция №2)
Программно-аппаратная защита (Лекция №2) Образовательная платформа Ё-стади
Образовательная платформа Ё-стади Виды памяти: назначение, принцип работы
Виды памяти: назначение, принцип работы Комплексное решение для НТ на базе JMeter
Комплексное решение для НТ на базе JMeter База данных Тимирязевский мукомольный комбинат
База данных Тимирязевский мукомольный комбинат Аниме. Соукок
Аниме. Соукок Контроль технического состояния оборудования – MRS Multi Resource
Контроль технического состояния оборудования – MRS Multi Resource Подготовка обучающихся к олимпиадам по информатике
Подготовка обучающихся к олимпиадам по информатике Инфо-Импульс
Инфо-Импульс