Содержание
- 2. Лекция 2. Дискретные и непрерывные модели ФГБОУ ВО «УлГПУ им. И.Н. Ульянова» Основы математической обработки информации
- 3. §1. Задача о размножении кроликов ФГБОУ ВО «УлГПУ им. И.Н. Ульянова» Основы математической обработки информации лектор
- 4. §1. Задача о размножении кроликов ФГБОУ ВО «УлГПУ им. И.Н. Ульянова» Основы математической обработки информации лектор
- 5. §1. Задача о размножении кроликов ФГБОУ ВО «УлГПУ им. И.Н. Ульянова» Основы математической обработки информации лектор
- 6. §1. Задача о размножении кроликов ФГБОУ ВО «УлГПУ им. И.Н. Ульянова» Основы математической обработки информации лектор
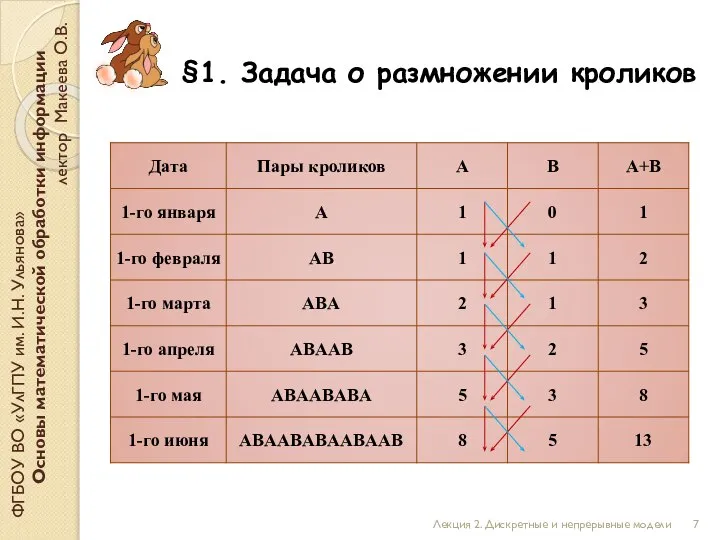
- 7. §1. Задача о размножении кроликов ФГБОУ ВО «УлГПУ им. И.Н. Ульянова» Основы математической обработки информации лектор
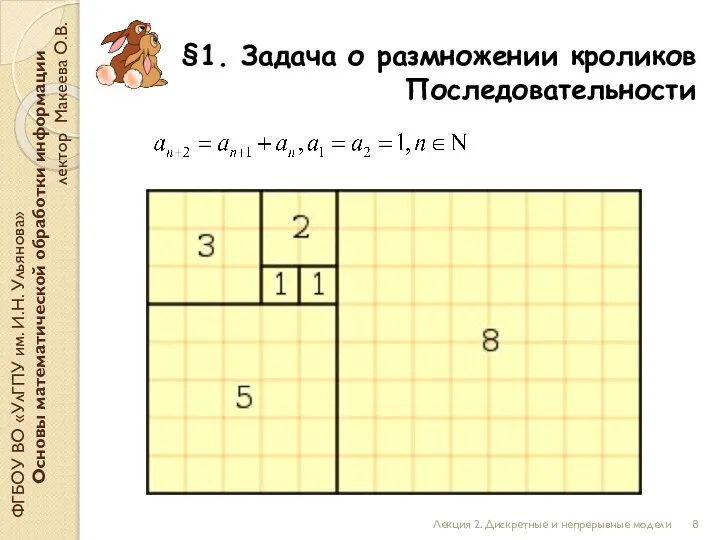
- 8. §1. Задача о размножении кроликов Последовательности ФГБОУ ВО «УлГПУ им. И.Н. Ульянова» Основы математической обработки информации
- 9. §1. Задача о размножении кроликов Последовательности ФГБОУ ВО «УлГПУ им. И.Н. Ульянова» Основы математической обработки информации
- 10. §1. Задача о размножении кроликов Последовательности ФГБОУ ВО «УлГПУ им. И.Н. Ульянова» Основы математической обработки информации
- 11. §1. Задача о размножении кроликов Последовательности ФГБОУ ВО «УлГПУ им. И.Н. Ульянова» Основы математической обработки информации
- 12. §2. Задача о ступеньках из домино ФГБОУ ВО «УлГПУ им. И.Н. Ульянова» Основы математической обработки информации
- 13. §2. Задача о ступеньках из домино ФГБОУ ВО «УлГПУ им. И.Н. Ульянова» Основы математической обработки информации
- 14. §2. Задача о ступеньках из домино ФГБОУ ВО «УлГПУ им. И.Н. Ульянова» Основы математической обработки информации
- 15. §2. Задача о ступеньках из домино ФГБОУ ВО «УлГПУ им. И.Н. Ульянова» Основы математической обработки информации
- 16. §2. Задача о ступеньках из домино Ряды ФГБОУ ВО «УлГПУ им. И.Н. Ульянова» Основы математической обработки
- 17. §2. Задача о ступеньках из домино Ряды ФГБОУ ВО «УлГПУ им. И.Н. Ульянова» Основы математической обработки
- 18. §2. Задача о ступеньках из домино Ряды ФГБОУ ВО «УлГПУ им. И.Н. Ульянова» Основы математической обработки
- 19. §3. Задача о площади сектора Функции ФГБОУ ВО «УлГПУ им. И.Н. Ульянова» Основы математической обработки информации
- 20. §3. Задача о площади сектора Функции ФГБОУ ВО «УлГПУ им. И.Н. Ульянова» Основы математической обработки информации
- 21. §3. Задача о площади сектора Функции ФГБОУ ВО «УлГПУ им. И.Н. Ульянова» Основы математической обработки информации
- 22. §3. Задача о площади сектора Функции ФГБОУ ВО «УлГПУ им. И.Н. Ульянова» Основы математической обработки информации
- 23. §3. Задача о площади сектора Функции ФГБОУ ВО «УлГПУ им. И.Н. Ульянова» Основы математической обработки информации
- 24. §3. Задача о площади сектора Функции ФГБОУ ВО «УлГПУ им. И.Н. Ульянова» Основы математической обработки информации
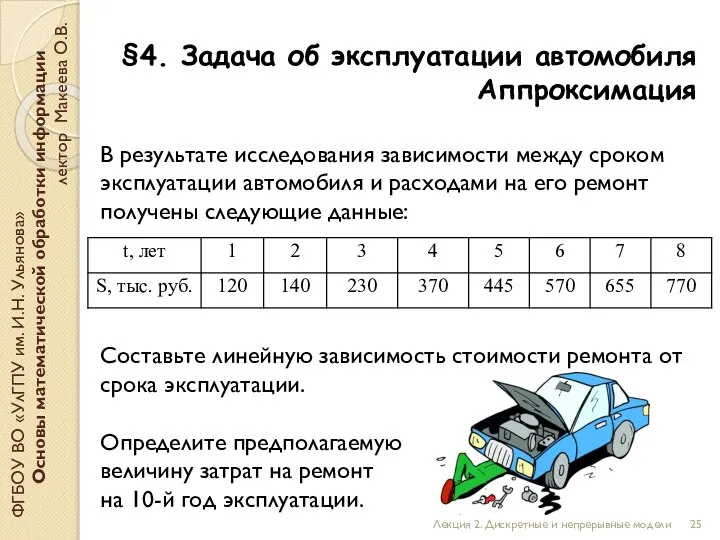
- 25. §4. Задача об эксплуатации автомобиля Аппроксимация ФГБОУ ВО «УлГПУ им. И.Н. Ульянова» Основы математической обработки информации
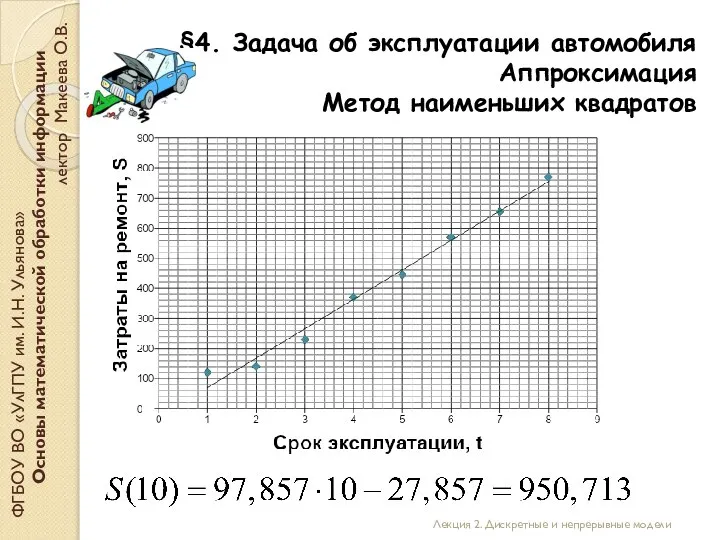
- 26. §4. Задача об эксплуатации автомобиля Аппроксимация ФГБОУ ВО «УлГПУ им. И.Н. Ульянова» Основы математической обработки информации
- 27. §4. Задача об эксплуатации автомобиля Аппроксимация ФГБОУ ВО «УлГПУ им. И.Н. Ульянова» Основы математической обработки информации
- 28. ФГБОУ ВО «УлГПУ им. И.Н. Ульянова» Основы математической обработки информации лектор Макеева О.В. Лекция 2. Дискретные
- 29. ФГБОУ ВО «УлГПУ им. И.Н. Ульянова» Основы математической обработки информации лектор Макеева О.В. Лекция 2. Дискретные
- 30. ФГБОУ ВО «УлГПУ им. И.Н. Ульянова» Основы математической обработки информации лектор Макеева О.В. Лекция 2. Дискретные
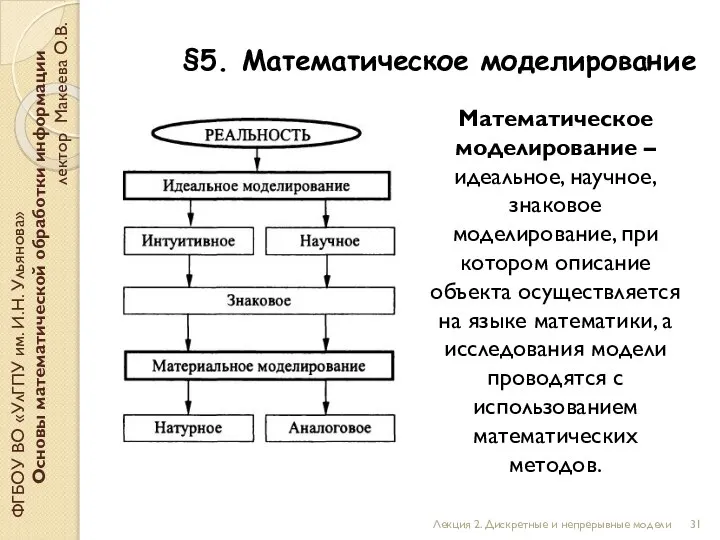
- 31. ФГБОУ ВО «УлГПУ им. И.Н. Ульянова» Основы математической обработки информации лектор Макеева О.В. Математическое моделирование –
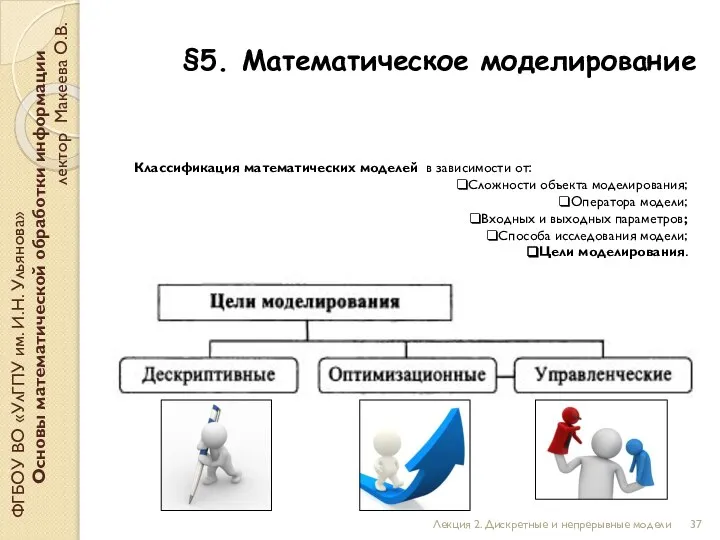
- 32. §5. Математическое моделирование ФГБОУ ВО «УлГПУ им. И.Н. Ульянова» Основы математической обработки информации лектор Макеева О.В.
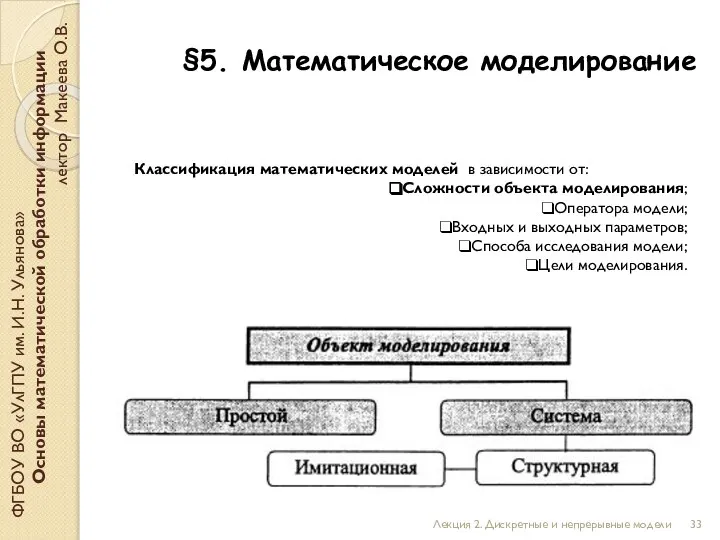
- 33. §5. Математическое моделирование ФГБОУ ВО «УлГПУ им. И.Н. Ульянова» Основы математической обработки информации лектор Макеева О.В.
- 34. §5. Математическое моделирование ФГБОУ ВО «УлГПУ им. И.Н. Ульянова» Основы математической обработки информации лектор Макеева О.В.
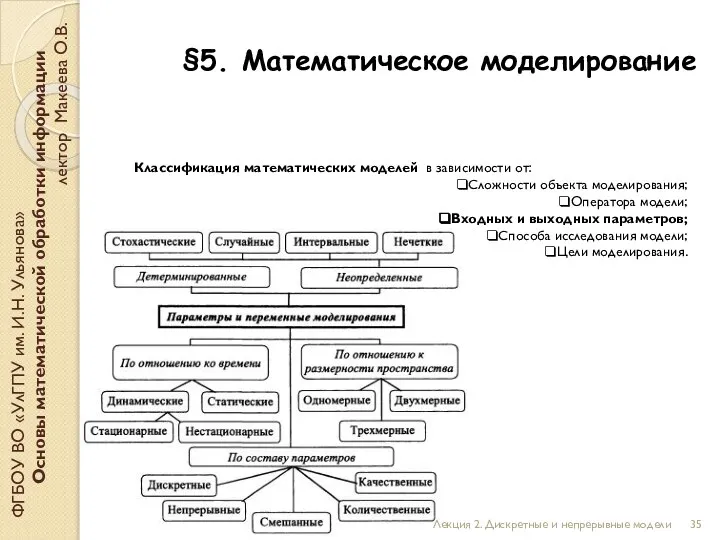
- 35. §5. Математическое моделирование ФГБОУ ВО «УлГПУ им. И.Н. Ульянова» Основы математической обработки информации лектор Макеева О.В.
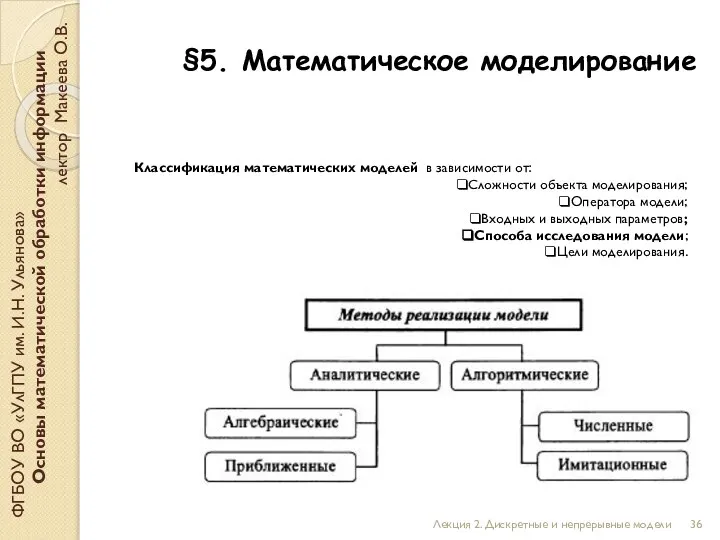
- 36. §5. Математическое моделирование ФГБОУ ВО «УлГПУ им. И.Н. Ульянова» Основы математической обработки информации лектор Макеева О.В.
- 37. §5. Математическое моделирование ФГБОУ ВО «УлГПУ им. И.Н. Ульянова» Основы математической обработки информации лектор Макеева О.В.
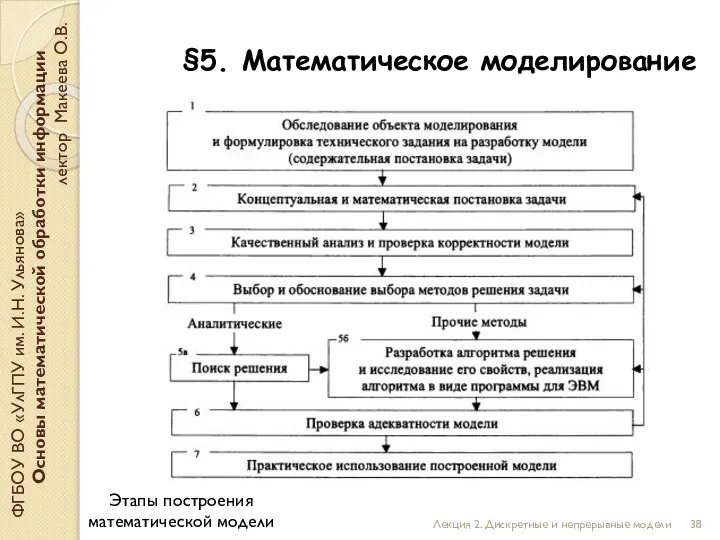
- 38. §5. Математическое моделирование ФГБОУ ВО «УлГПУ им. И.Н. Ульянова» Основы математической обработки информации лектор Макеева О.В.
- 39. ФГБОУ ВО «УлГПУ им. И.Н. Ульянова» Основы математической обработки информации лектор Макеева О.В. Абатурова Вера Сергеевна
- 40. ФГБОУ ВО «УлГПУ им. И.Н. Ульянова» Основы математической обработки информации лектор Макеева О.В. а - количество
- 42. Скачать презентацию





























 Предметная неделя ИНФОРМАТИКИ
Предметная неделя ИНФОРМАТИКИ Многоуровневые справочники. Практическая работа /блок №2
Многоуровневые справочники. Практическая работа /блок №2 Внешние носители информации
Внешние носители информации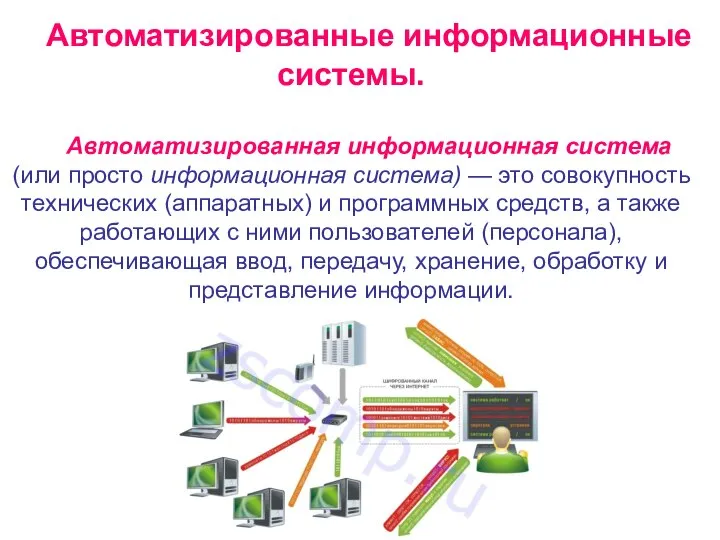 Автоматизированные информационные системы
Автоматизированные информационные системы Требования к информационным стендам
Требования к информационным стендам Java_amm_lesson_3
Java_amm_lesson_3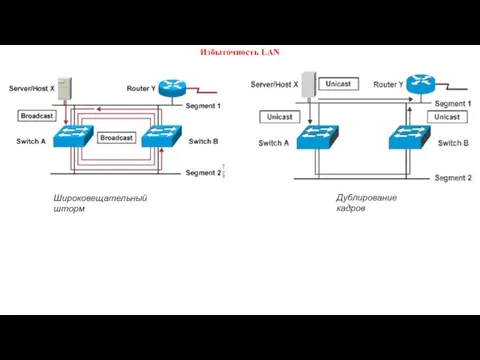 Избыточность LAN. Широковещательный шторм. Дублирование кадров
Избыточность LAN. Широковещательный шторм. Дублирование кадров Информационные системы и программирование
Информационные системы и программирование Дз перевод из 2-й в 8-ую и 16-ю системы счисления (самостоятельно разобрать)
Дз перевод из 2-й в 8-ую и 16-ю системы счисления (самостоятельно разобрать) Информация и ее свойства
Информация и ее свойства Текстовые редакторы
Текстовые редакторы Блок Экран. Занятие 3
Блок Экран. Занятие 3 Инструкция по работе с ЭБС BOOK.RU
Инструкция по работе с ЭБС BOOK.RU Рекламное продвижение с помощью Instagram: стратегия, контент, вовлечение и клиенты
Рекламное продвижение с помощью Instagram: стратегия, контент, вовлечение и клиенты Поняття життєвого циклу програмного забезпечення та етапи розробки програмного забезпечення. Тема 1
Поняття життєвого циклу програмного забезпечення та етапи розробки програмного забезпечення. Тема 1 Программа Adobe Photoshop
Программа Adobe Photoshop Ссылка для скачивания презентации
Ссылка для скачивания презентации Проектирование коммуникаций и вычислений
Проектирование коммуникаций и вычислений Инжиниринг биотехнологических процессов и систем. Практики, стандарты и терминология. (Лекция 3)
Инжиниринг биотехнологических процессов и систем. Практики, стандарты и терминология. (Лекция 3) Введение в WCF
Введение в WCF 04 Классы
04 Классы Опыт взаимодействия с недоступными интерфейсами
Опыт взаимодействия с недоступными интерфейсами Арифметические и логические основы вычислительной техники
Арифметические и логические основы вычислительной техники Облачные технологии
Облачные технологии 7_pascal_sortirovka_massiva
7_pascal_sortirovka_massiva Проект CryptoShock. Описание, планы, перспективы
Проект CryptoShock. Описание, планы, перспективы 基于XCP和puppet的虚拟化云平台建设 演讲人
基于XCP和puppet的虚拟化云平台建设 演讲人 Разработка модулей программного обеспечения для компьютерных систем
Разработка модулей программного обеспечения для компьютерных систем