Содержание
- 3. Матричные операции Пусть матрица А(МхN) умножается на матрицу B(NxK). Результат – матрица С В покомпонентной записи:
- 4. Специальные операции На Матлабе это выглядит как: Здесь X и Y – вектор-столбцы Аналогично выглядят операции:
- 5. Задание Дана покомпонентная запись. Записать в формате Матлаба: А – матрица, х и y– вектор-столбцы. Записать
- 6. Логическая индексация массивов Логические вектора, построенные с помощью логических выражений могут служить индексами при доступе к
- 7. Пусть функция задается разными выражениями при разных значениях аргумента: >> y=@(x)[0*x((x >>x=-10:0.1:10; >>plot(x,y(x)) Обратите внимание как
- 8. Создание матриц с заданными свойствами eye(n) – возвращает единичную матрицу размера nxn; eye(m,n) – размера mxn.
- 9. Функция linspace формирует линейный массив равноотстоящих узлов. Это подобно оператору :, но дает прямой контроль над
- 10. >> linspace(1,10,5) ans = 1.0000 3.2500 5.5000 7.7500 10.0000 logspace(a,b) – возвращает вектор-строку из 50 равноотстоящих
- 11. >> logspace(1,10,5) ans = Columns 1 through 4: 10.00000 1778.27941 316227.76602 56234132.51903 Column 5: 10000000000.00000 Функция
- 12. Функция randn генерирует массив со случайными элементами, распределенными по нормальному закону с нулевым математическим ожиданием и
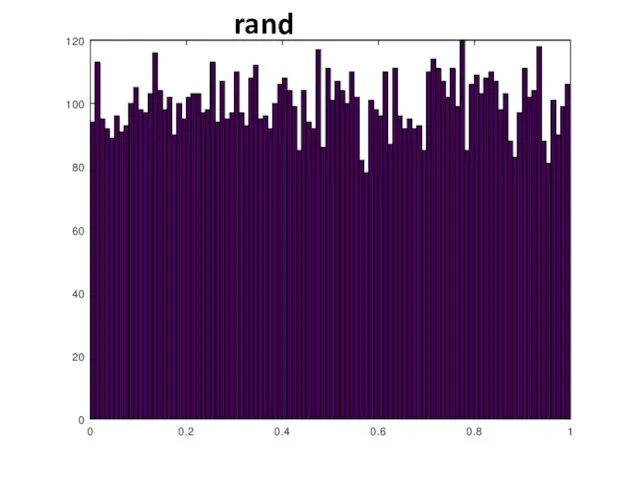
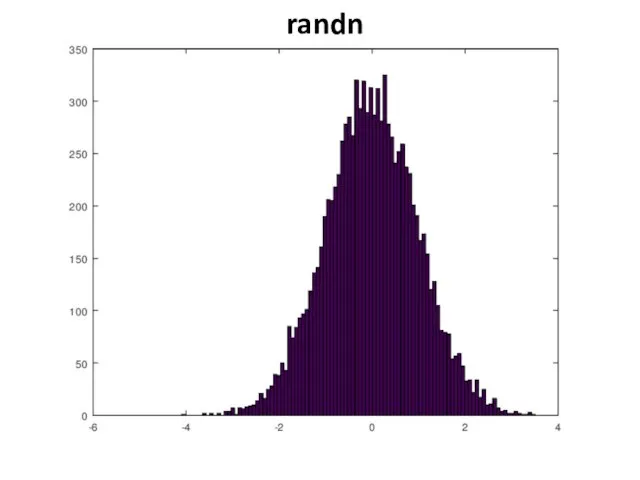
- 13. Проверить распределение случайных чисел можно, построив гистограмму распределения большого количества чисел. >> Y=rand(10000,1); hist(Y,100) >> Y=randn(10000,1);
- 14. rand
- 15. randn
- 16. Конкатенация матриц C = cat(dim,A,B) – объединяет массивы А и B в соответствии со спецификацией размерности
- 17. X = diag(v,k) – для вектора v, состоящего из n компонентов, возвращает квадратную матрицу Х порядка
- 18. • prod(A) – возвращает произведение элементов массива, если А – вектор, или вектор-строку, содержащую произведения элементов
- 19. Пример: >> A=[1 2 3 4; 2 4 5 7; 6 8 3 4] A =
- 20. • sum(A) – возвращает сумму элементов массива, если А – вектор, или вектор-строку, содержащую сумму элементов
- 21. >> X=[1 2;3 4] X = 1 2 3 4 >> sum(X) ans = 4 6
- 22. Возможно создание пустых матриц, например: >> M=[] M = [](0x0) >> M=[M [1,2;3,4]] M = 1
- 23. Матричные функции expm(X) – возвращает еxp(X) от квадратной матрицы Х. sqrtm(X),logm(X) – квадратный корень и логарифм
- 24. >> S=[1,0,3;1,3,1;4,0,0] >> a=expm(S) a = 31.22028 0.00000 23.37787 38.96594 20.08554 30.05928 31.17049 0.00000 23.42766 >>
- 25. Умножение матриц
- 26. Вычисление нормы и чисел обусловленности матрицы Норма вектора X (или, точнее, его p-норма) задается выражением и
- 27. Пусть А – матрица. Тогда n=norm(A) эквивалентно n=norm(A,2) и возвращает вторую норму, то есть самое большое
- 28. >> A=[2,3,1;1,9,4;2,6,7] A = 2 3 1 1 9 4 Проверьте! 2 6 7 >> norm(A)
- 29. Число обусловленности матрицы определяет чувствительность решения системы линейных уравнений к погрешностям исходных данных. Следующая функция позволяет
- 30. >> A=hilb(4) A = 1.00000 0.50000 0.33333 0.25000 0.50000 0.33333 0.25000 0.20000 0.33333 0.25000 0.20000 0.16667
- 31. Для нахождения определителя (детерминанта) и ранга матриц в MATLAB имеются следующие функции: • det(X) – возвращает
- 32. Ранг матрицы определяется количеством сингулярных чисел, превышающих порог tol. Для вычисления ранга используется функция rank: rank(A)
- 33. >> A=hilb(11); >> rank(A) ans = 10 >> cond(A) ans = 5.2237e+14
- 34. Вычисление ортонормированного базиса матрицы обеспечивают следующие функции: • B = orth(A) – возвращает ортонормированный базис матрицы
- 35. Собственные значения и собственные векторы квадратной матрицы Задача на собственные значения для квадратной матрицы имеет вид:
- 36. Совокупность всех собственных векторов, относящихся к одному и тому же собственному значению, вместе с нулевым вектором,
- 37. Матрица А приводима к диагональному виду тогда и только тогда, когда существует базис в n-мерном пространстве,
- 38. Матрица А называется неотрицательно определенной, если: Для любого вектора Х Матрица А называется симметрической, если: Ан
- 39. [V, lambda] = eig (A) – вычисление матрицы собственных векторов (V) и диагональной матрицы собственных значений
- 40. >> V'*V ans = 1.0000e+00 -2.7343e-01 5.5511e-17 -2.7343e-01 1.0000e+00 -9.9920e-16 5.5511e-17 -9.9920e-16 1.0000e+00 Матрица А2 –
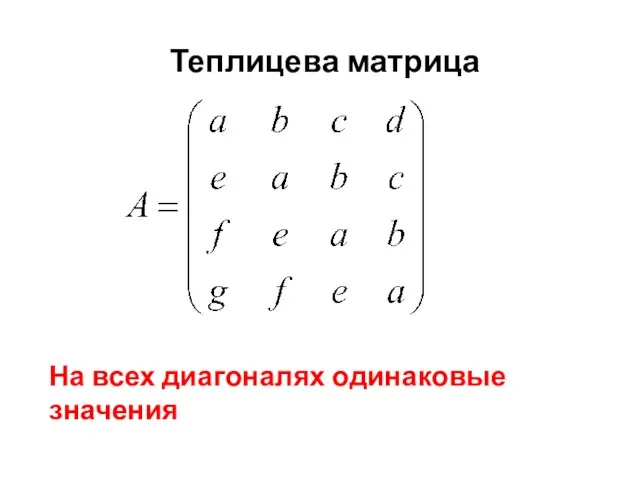
- 41. Теплицева матрица На всех диагоналях одинаковые значения
- 42. toeplitz (c) toeplitz (c, r) Возвращает матрицу Теплица созданную из вектора c (в первом случае). Во
- 43. Создадим матрицу >> r=0.9; >> n=5;a=(0:n-1).^2; >> c=r.^a; >> K=toeplitz (c) K = 1.00000 0.90000 0.65610
- 44. Найдем собственные вектора и собственные значения этой матрицы >> [V,D]=eig(K); V = -1.6166e-01 3.8166e-01 5.7288e-01 -5.9526e-01
- 45. >> V'*V ans = 1.0000e+00 1.1102e-16 6.9389e-17 -4.1633e-17 -9.0206e-17 1.1102e-16 1.0000e+00 -1.6653e-16 5.5511e-17 5.5511e-17 6.9389e-17 -1.6653e-16
- 46. Скорость выполнения Файл test1 Файл test2 A=rand(1000,1000); A=rand(1000,1000); B=rand(1000,1000); B=rand(1000,1000); for i=1:1000 A=A.^B; for j=1:1000 A(i,j)=A(i,j).^B(i,j);
- 47. A=rand(1000,1000); B=rand(1000,1000); for i=1:1000 for j=1:1000 A(i,j)=A(i,j).^B(i,j); end end --------------------------------- >> clear >> tic,test1,toc Elapsed time
- 48. >> clear >> tic,test1,toc Elapsed time is 0.340472 seconds. >> clear >> tic,test2,toc Elapsed time is
- 50. Скачать презентацию

















![>> X=[1 2;3 4] X = 1 2 3 4 >> sum(X) ans = 4 6](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/877530/slide-20.jpg)
![Возможно создание пустых матриц, например: >> M=[] M = [](0x0) >> M=[M](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/877530/slide-21.jpg)

![>> S=[1,0,3;1,3,1;4,0,0] >> a=expm(S) a = 31.22028 0.00000 23.37787 38.96594 20.08554 30.05928](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/877530/slide-23.jpg)



![>> A=[2,3,1;1,9,4;2,6,7] A = 2 3 1 1 9 4 Проверьте! 2](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/877530/slide-27.jpg)










![[V, lambda] = eig (A) – вычисление матрицы собственных векторов (V) и](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/877530/slide-38.jpg)



![Найдем собственные вектора и собственные значения этой матрицы >> [V,D]=eig(K); V =](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/877530/slide-43.jpg)




 Турнир по Call of duty mobile
Турнир по Call of duty mobile Локальная сеть
Локальная сеть Пошаговая инструкция по работе с шаблонами в АИП Пилотный проект веб-портала НБ РК
Пошаговая инструкция по работе с шаблонами в АИП Пилотный проект веб-портала НБ РК Режимы построения объектов. Использование режимов ОРТО и ПОЛЯР
Режимы построения объектов. Использование режимов ОРТО и ПОЛЯР Операційні та файлові системи. Операційна система Windows XP Professional
Операційні та файлові системи. Операційна система Windows XP Professional Ближе к клиенту
Ближе к клиенту Инструкция по регистрации на курсе ПП
Инструкция по регистрации на курсе ПП 在pc机上打开 direct USB
在pc机上打开 direct USB Выбор валюты в документах внутреннего товародвижения
Выбор валюты в документах внутреннего товародвижения Склейка карт по фотографиям
Склейка карт по фотографиям Системы счисления
Системы счисления Алгоритмизация и программирование. Кафедра информатики Барнаул 2021
Алгоритмизация и программирование. Кафедра информатики Барнаул 2021 Комп'ютерні віруси
Комп'ютерні віруси Модуль. Модульная Сетка
Модуль. Модульная Сетка Администрирование СКЗИ
Администрирование СКЗИ Двумерные массивы
Двумерные массивы Основы моделирования схем в программе Electronics Workbench 512
Основы моделирования схем в программе Electronics Workbench 512 Разноцветные истории. Обзор альбомов отдела хранения основного фонда библиотеки
Разноцветные истории. Обзор альбомов отдела хранения основного фонда библиотеки Процедурное программирование 01_09_2021
Процедурное программирование 01_09_2021 Исследование топологии двумерных многообразий с помощью графического редактора Blender
Исследование топологии двумерных многообразий с помощью графического редактора Blender Массовая оптимизация запросов PostgreSQL – explain.sbis.ru
Массовая оптимизация запросов PostgreSQL – explain.sbis.ru Bakshaev
Bakshaev Классы. Описание класса
Классы. Описание класса Изучение работы программируемых логических контроллеров. Лабораторная работа №1
Изучение работы программируемых логических контроллеров. Лабораторная работа №1 Массивы в С#
Массивы в С# Компьютерные игры и сети как развлечение
Компьютерные игры и сети как развлечение İntellektual sistemlər
İntellektual sistemlər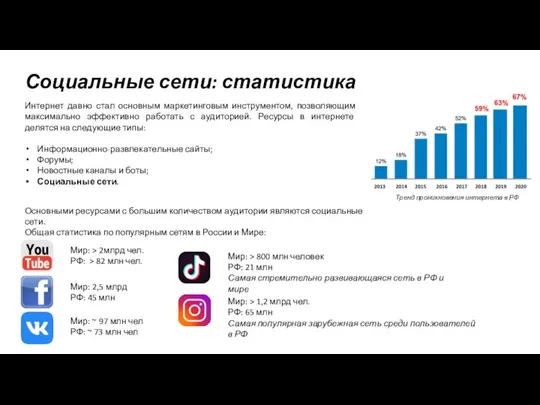 Социальные сети: статистика
Социальные сети: статистика