Содержание
- 2. PROBABILITATE?
- 3. Ce este probabilitatea? Probabilitatea este un concept care estimează răspunsul la întrebarea: “Se va produce oare
- 4. Definiții și notații Probabilitatea este adesea asociată cu cel puțin un eveniment aruncarea zarului bile negre/roșii
- 6. Prin urmare, vrem să știm care este probabilitatea că X = 3 „Care este probabilitatea?” –
- 7. Cele 3 tipuri de probabilitate Probabil că primul lucru care trebuie înțeles este că există diferite
- 8. Probabilitate marginală Dacă A este un eveniment, atunci probabilitatea marginală este probabilitatea ca acel eveniment să
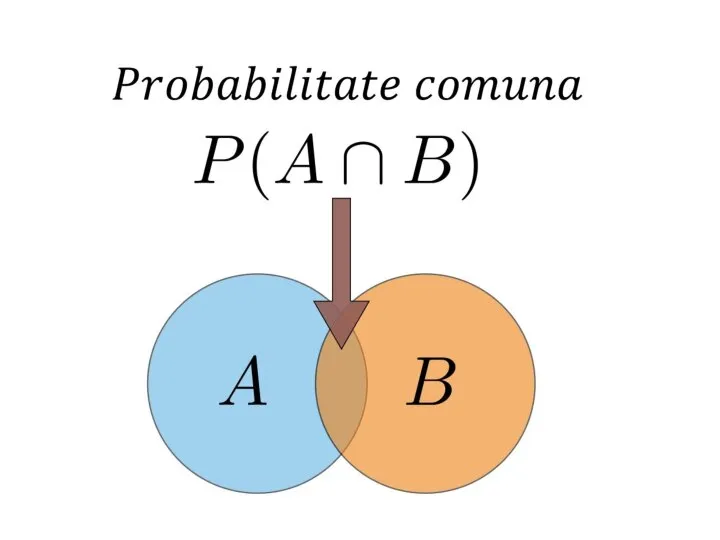
- 9. Probabilitate comună Probabilitatea a două evenimente care sunt intersectate Dacă A și B sunt două evenimente,
- 11. Probabilitate condiționată Probabilitatea ca un eveniment să aibă loc știind că alte evenimente au avut deja
- 12. Legarea celor 3 tipuri
- 13. Explicații Uneori, distincția dintre probabilitatea comună și probabilitatea condiționată poate fi destul de confuză, așa că
- 14. În cazul în care dorim să găsim probabilitatea de a extrage o carte care este roșie
- 15. În cazul în care dorim să găsim probabilitatea de a extrage o carte care este 4
- 17. Inferența Bayesiană Înainte de a introduce inferența bayesiană, este necesar să înțelegem teorema lui Bayes Cunoștințe
- 18. Definiția matematică
- 19. Exemplu În pachet sunt 52 de cărți, 26 dintre ele sunt roșii și 26 negre. Care
- 21. Cum ne permite teorema lui Bayes să încorporăm observările anterioare?
- 25. Acum știm care este teorema lui Bayes și cum să o folosim, putem începe să răspundem
- 26. Inferența este procesul de distribuire a probabilității din date Inferența bayesiană este, așadar, doar procesul de
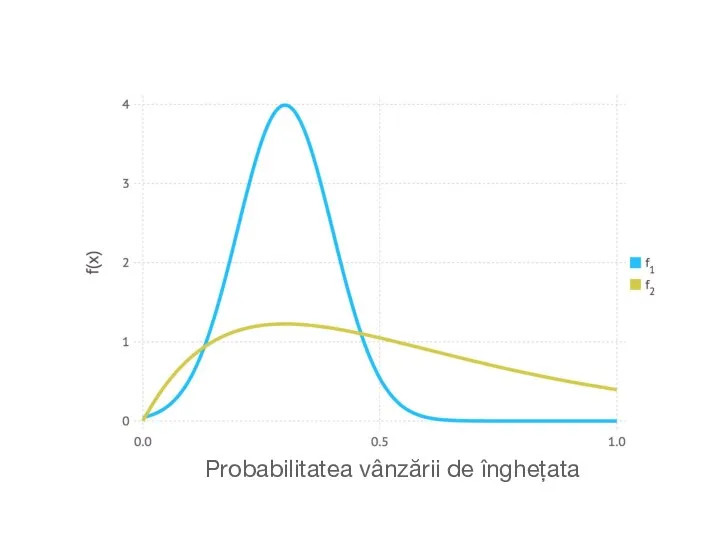
- 27. În exemplul de înghețată de mai sus, am văzut că probabilitatea anterioară de a vinde înghețată
- 28. Probabilitatea vânzării de înghețata
- 29. Modelul teoremei lui Bayes În loc de evenimentul A, vom vedea de obicei Θ, acest simbol
- 31. Am văzut că P (Θ) este distribuția anterioară. Reprezintă observările noastre despre adevărata valoare a parametrilor,
- 32. P (Θ | data) din partea stângă este cunoscută sub numele de distribuție posterioară. Aceasta este
- 33. TEORIA PROBABILITĂȚII & ML În general vorbind, teoria probabilității este studiul matematic al incertitudinii. Acesta joacă
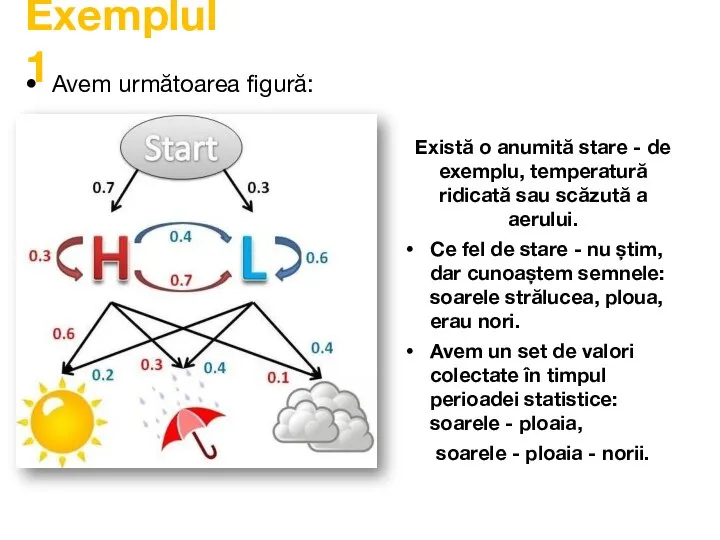
- 34. Exemplul 1 Avem următoarea figură: Există o anumită stare - de exemplu, temperatură ridicată sau scăzută
- 35. Exemplul 1 Numerele de deasupra săgeților sunt probabilități, adică : dacă este însorit, atunci cu o
- 36. Din exemplul anterior concluzionăm că ML întipărește informația statistică pe o perioadă studiată, fie zile, luni,
- 37. Scurt istoric Pentru prima dată abordări probabiliste în Machine Learning au avut loc în anii ’90
- 38. Abordări probabiliste: Bayes Abordarea Bayes este cea mai academică viziune a învățării mașinilor. Acest lucru este
- 39. Abordări probabiliste: Bayes Pentru că oferă o descriere matematică clară a formării și a estimărilor numerice
- 40. Avem notațiile: P(h) - probabilitatea că se petrece evenimentul h (h, în acest caz nu este
- 41. Teorema lui Bayes este o consecință a afirmației evidente: P(A^B)=P(A\B)P(B)=P(B\A)P(A) Adică: Bineînțeles, P (B) trebuie să
- 42. Fie că notăm datele noastre – D, iar ipotezele noastre – h. Atunci trebuie să găsim
- 43. Suntem interesați doar de relația de probabilitate, deci putem elimina P(D) din această expresie (D nu
- 44. Până ce nu avem nici date concrete, nici mulțimea ipotezelor. Hai să le inventăm.
- 45. Exemplul 2 Să presupunem că am extras N=3 mere: R=1 roșii și G=2 verzi. Să prezentăm
- 46. Notăm prin R0 și G0 numărul de mere roșii și verzi din coș. În câte moduri
- 47. Atunci probabilitatea căutată este egală cu: A rămas să aplicăm aceasta (probabilitatea) la ipotezele noastre: ipoteza
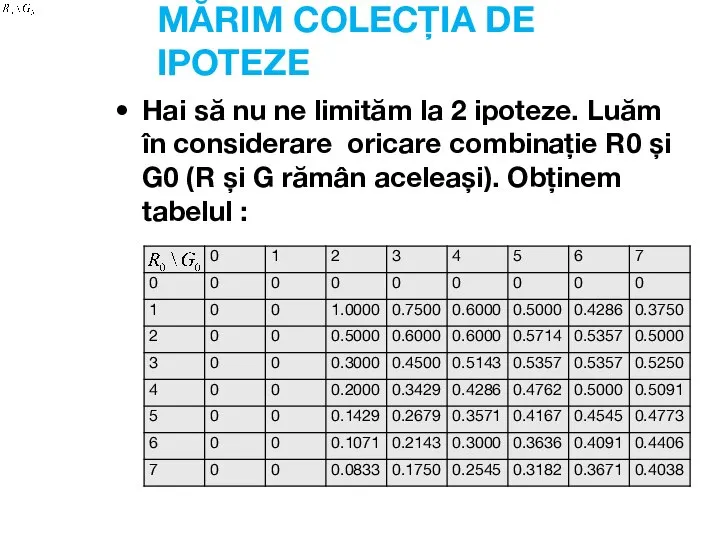
- 48. MĂRIM COLECȚIA DE IPOTEZE Hai să nu ne limităm la 2 ipoteze. Luăm în considerare oricare
- 49. Se observă 2 probleme: Problema mai mică: multe ipoteze au aceeași probabilitate (De ex: și )
- 50. Inteligența artificială a noastră a învățat pe de rost toate datele de învățare. Cel mai probabil
- 51. Să presupunem că știm de undeva că în coș se află doar 6, 7 sau 8
- 53. Скачать презентацию

























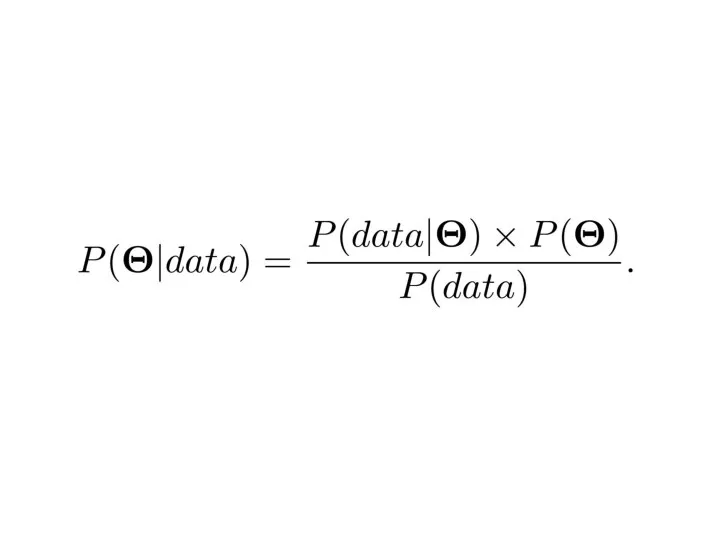



















 Презентация на тему Интерференция света (11 класс)
Презентация на тему Интерференция света (11 класс)  Основные понятия баз данных
Основные понятия баз данных Особенности текстов разных типов
Особенности текстов разных типов Регистрация в Moodle: пошаговая инструкция
Регистрация в Moodle: пошаговая инструкция Уютная библиотека. Защита проекта
Уютная библиотека. Защита проекта Флагман телеком. Базовое знание технологий и сетей
Флагман телеком. Базовое знание технологий и сетей Кодирование информации
Кодирование информации Что такое флэш-память?
Что такое флэш-память? Программирование циклов Цикл while
Программирование циклов Цикл while Руководство по использованию активов в сети Ethereum через платформу Flamingo
Руководство по использованию активов в сети Ethereum через платформу Flamingo Как преуспеть в тестировании
Как преуспеть в тестировании Социальные сети - это зло
Социальные сети - это зло Анимация летящего снега
Анимация летящего снега Оборудование компьютера
Оборудование компьютера Автоматизированная информационная система Автосервис
Автоматизированная информационная система Автосервис Лекция 1
Лекция 1 Безопасный интернет
Безопасный интернет Маруся. Использование голосового помощника на уроках
Маруся. Использование голосового помощника на уроках Российская СПС Консультант Плюс. Лекция 22
Российская СПС Консультант Плюс. Лекция 22 Символ собака
Символ собака Примеры и перспективы использования цифровых каналов связи
Примеры и перспективы использования цифровых каналов связи Технологии обработки и анализа информации в табличном процессоре MS Excel
Технологии обработки и анализа информации в табличном процессоре MS Excel Интернет-сервисы ЦНСХБ
Интернет-сервисы ЦНСХБ Біоінформатика. Бази даних. Модель NCBI. Lab.1
Біоінформатика. Бази даних. Модель NCBI. Lab.1 Как влияют социальные сети на обучение
Как влияют социальные сети на обучение Новая социальная сеть benefit.com. Презентация для инвесторов
Новая социальная сеть benefit.com. Презентация для инвесторов Ms word. Форматирование документа. Установка параметров шрифта и абзаца, создание границ
Ms word. Форматирование документа. Установка параметров шрифта и абзаца, создание границ Создание и оформление презентации (задания)
Создание и оформление презентации (задания)