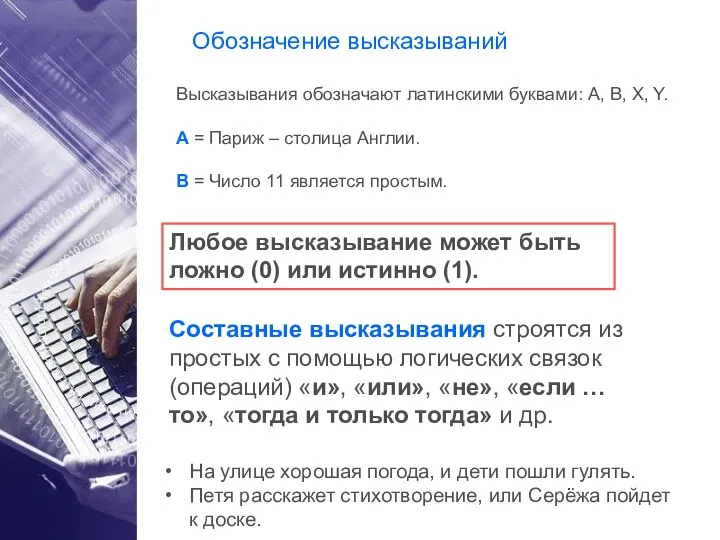
Содержание
- 2. Основные понятия алгебры логики Процессор выполняет арифметические и логические операции над двоичными кодами. Поэтому для получения
- 3. Second Page Your Text here Lorem ipsum dolor sit amet, consectetuer adipiscing elit, sed diam nonummy
- 4. Second Page Your Text here Lorem ipsum dolor sit amet, consectetuer adipiscing elit, sed diam nonummy
- 5. Second Page Your Text here Lorem ipsum dolor sit amet, consectetuer adipiscing elit, sed diam nonummy
- 6. Second Page Your Text here Lorem ipsum dolor sit amet, consectetuer adipiscing elit, sed diam nonummy
- 7. Second Page Your Text here Lorem ipsum dolor sit amet, consectetuer adipiscing elit, sed diam nonummy
- 8. Second Page Your Text here Lorem ipsum dolor sit amet, consectetuer adipiscing elit, sed diam nonummy
- 9. Таблицы истинности Все операции алгебры логики определяются таблицами истинности значений. Таблица истинности определяет значение сложного высказывания
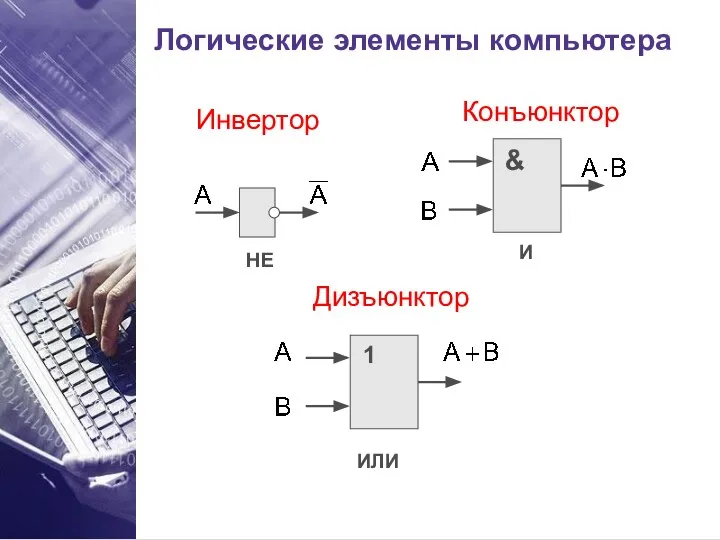
- 10. Инверсия - логическое отрицание Логическое отрицание делает истинное высказывание ложным и, наоборот, ложное – истинным. А=
- 11. Конъюнкция - логическое умножение Результат логического умножения является истинным тогда и только тогда, когда истинны все
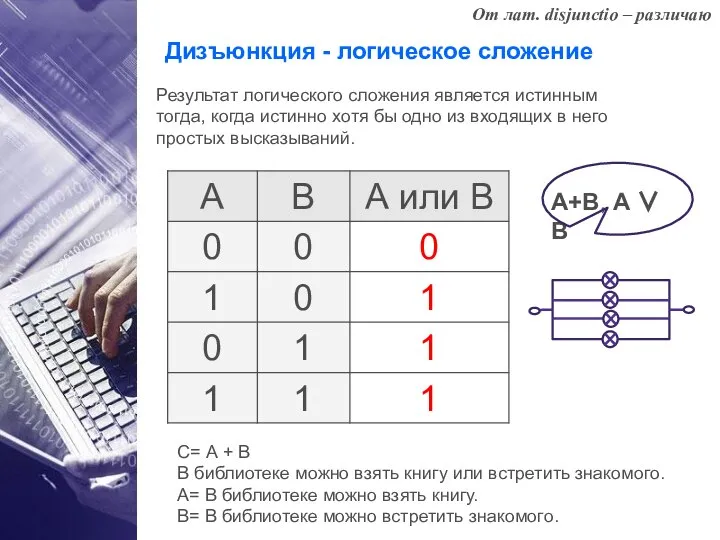
- 12. Дизъюнкция - логическое сложение Результат логического сложения является истинным тогда, когда истинно хотя бы одно из
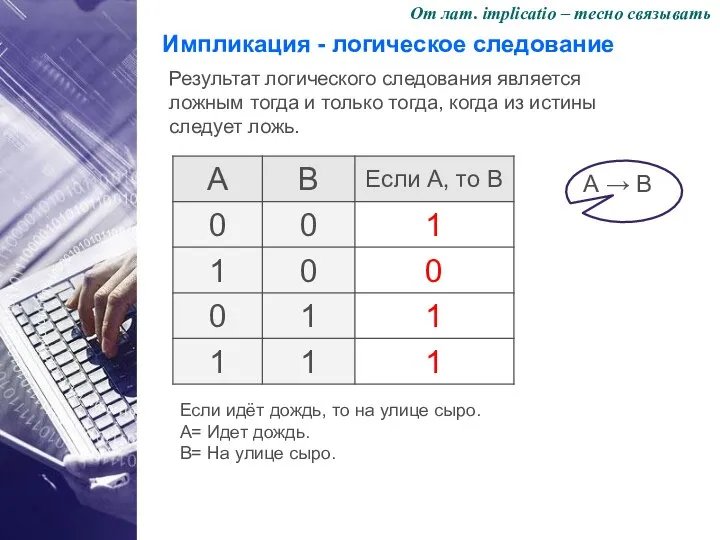
- 13. Импликация - логическое следование Результат логического следования является ложным тогда и только тогда, когда из истины
- 14. Эквивалентность - логическое равенство Результат логического равенства является истинным тогда и только тогда, когда оба высказывания
- 15. Домашнее задание Выучить пять таблиц истинности с определениями логических операций.
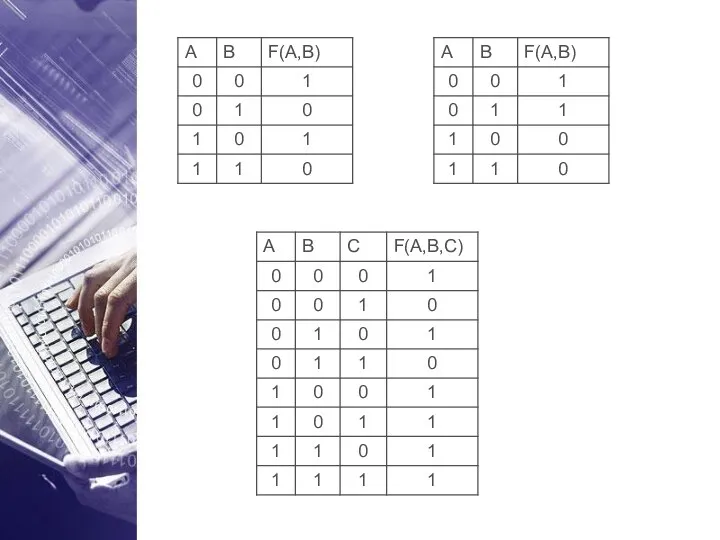
- 16. Составление таблиц истинности по логической формуле
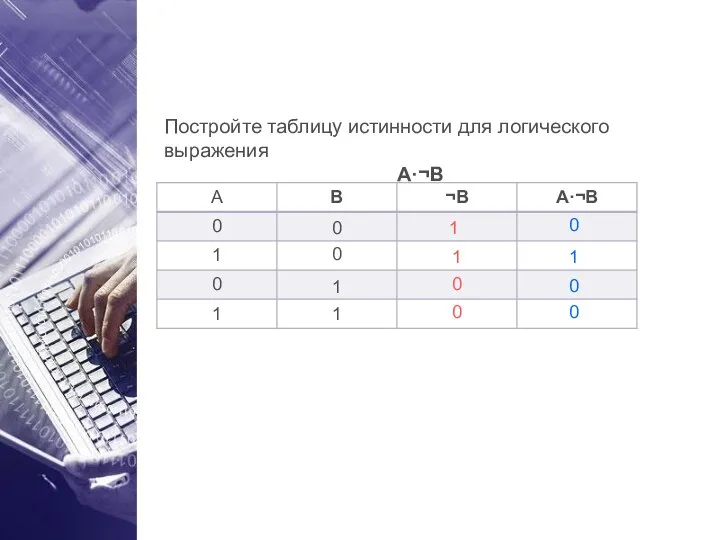
- 17. Постройте таблицу истинности для логического выражения A·¬B 1 1 0 0 0 0 0 1 0
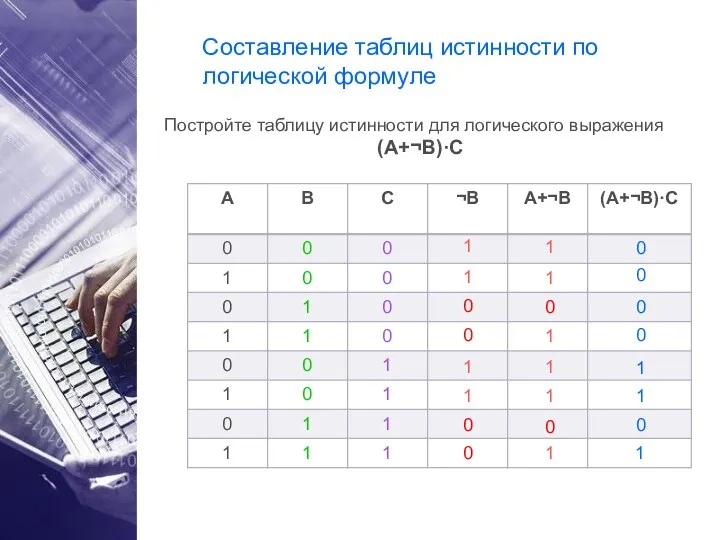
- 18. Составление таблиц истинности по логической формуле Постройте таблицу истинности для логического выражения (A+¬B)·C 1 1 1
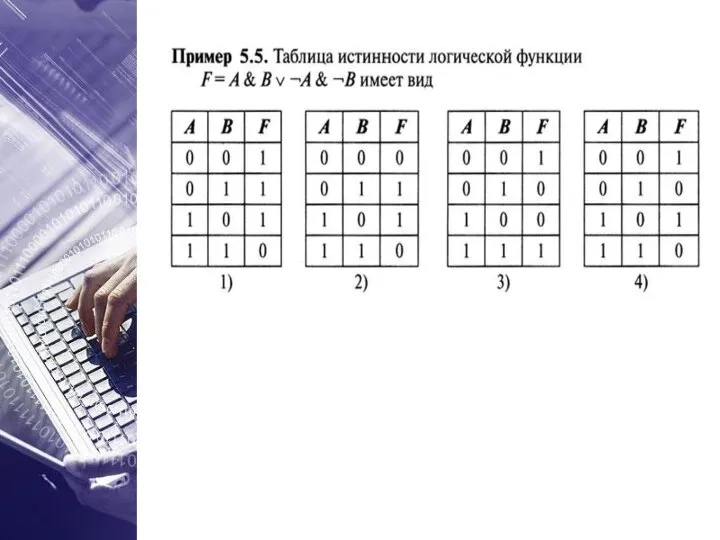
- 19. ОПРЕДЕЛЕНИЕ ЛОГИЧЕСКОГО ВЫРАЖЕНИЯ ПО ТАБЛИЦЕ ИСТИННОСТИ
- 20. Условимся называть задачу построения таблицы истинности по формуле сложного высказывания – прямой задачей. Тогда обратная задача
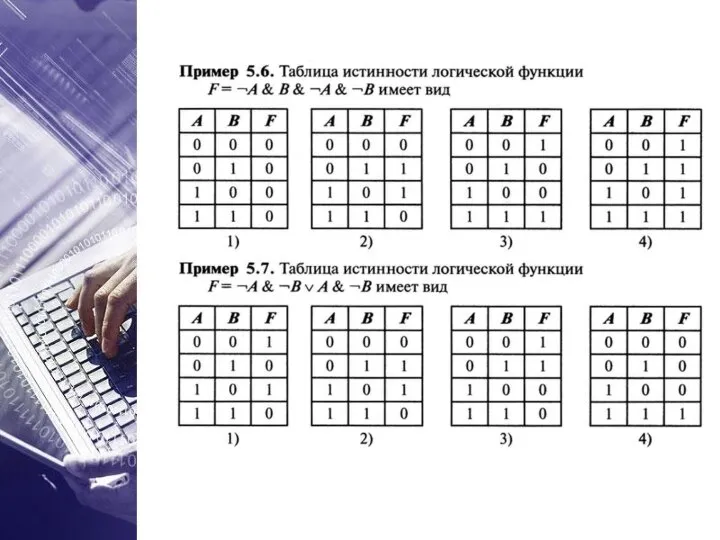
- 21. 1. Выделить в таблице истинности строки, в которых выражение истинно (1); ✔ ✔ Алгоритм нахождения искомой
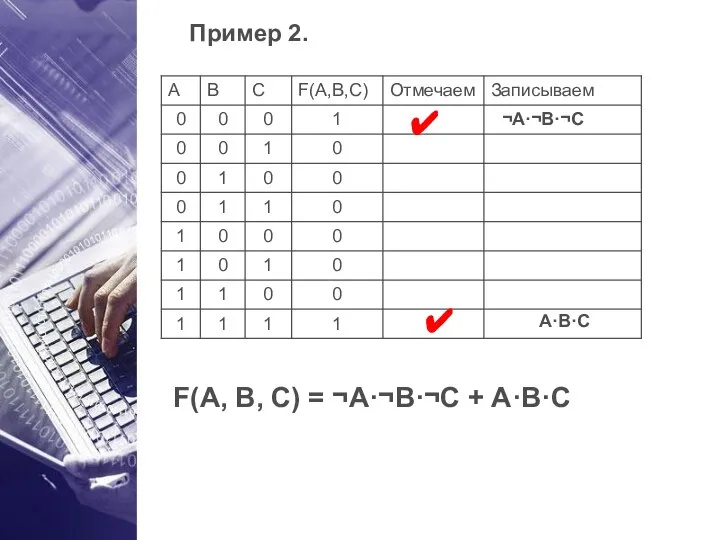
- 22. Пример 2. ✔ ✔ ¬A·¬B·¬C A·B·C F(A, B, C) = ¬A·¬B·¬C + A·B·C
- 23. Пример 3. ✔ ✔ ¬ A · B A · B F(A, B) = ¬A·B +
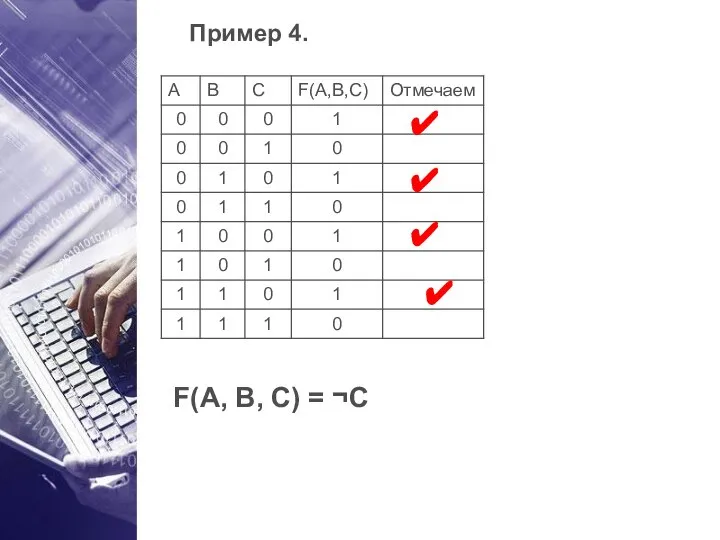
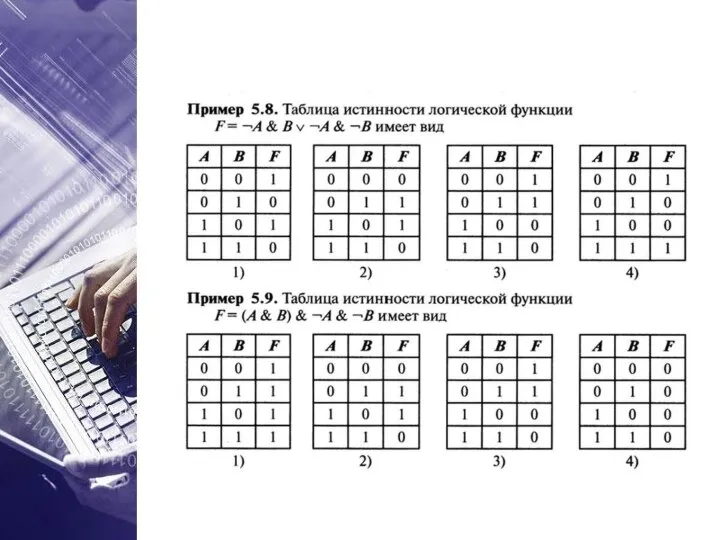
- 24. Пример 4. ✔ ✔ F(A, B, C) = ¬C ✔ ✔
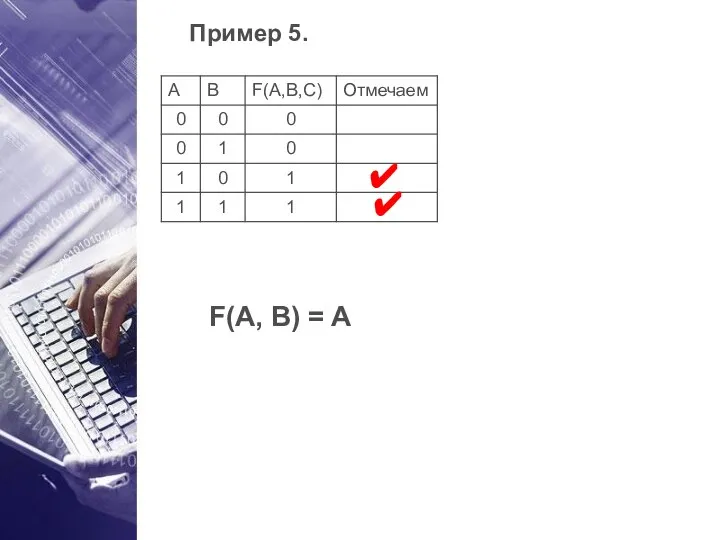
- 25. Пример 5. ✔ F(A, B) = A ✔
- 27. ЗАДАНИЯ ИЗ ГИА
- 28. Задания из ГИА Для какого из указанных значений числа Х истинно выражение (X 2))? 1) 1
- 33. Логические элементы и логические схемы компьютера. Как при строительстве дома применяют различного рода типовые блоки: кирпичи,
- 34. Электронным элементом называется соединение различных деталей – в первую очередь, диодов и транзисторов, а также резисторов,
- 35. Логические элементы компьютера НЕ И ИЛИ Инвертор Конъюнктор Дизъюнктор
- 36. Тысячи микроскопических электронных переключателей в кристалле интегральной схемы сгруппированы в системы, выполняющие логические операции, т. е.
- 37. Электронным элементом называется соединение различных деталей – в первую очередь, диодов и транзисторов, а также резисторов,
- 38. Построение логических схем Определить число логических переменных. Определить количество базовых логических операций и их порядок. Изобразить
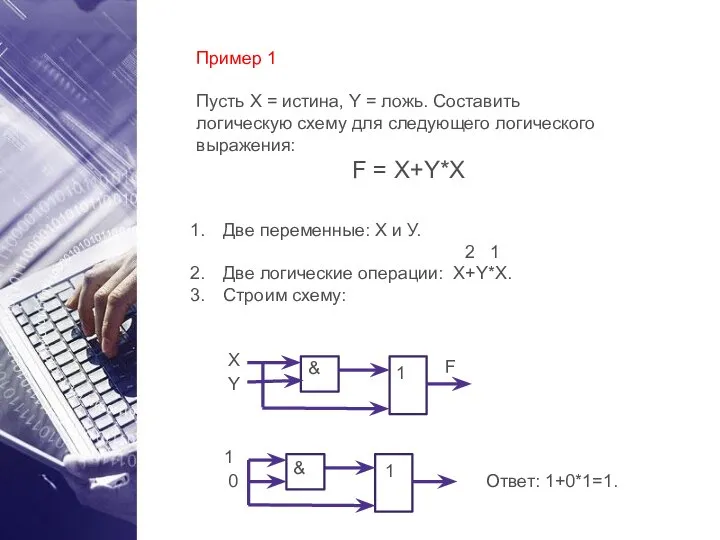
- 39. Пример 1 Пусть X = истина, Y = ложь. Составить логическую схему для следующего логического выражения:
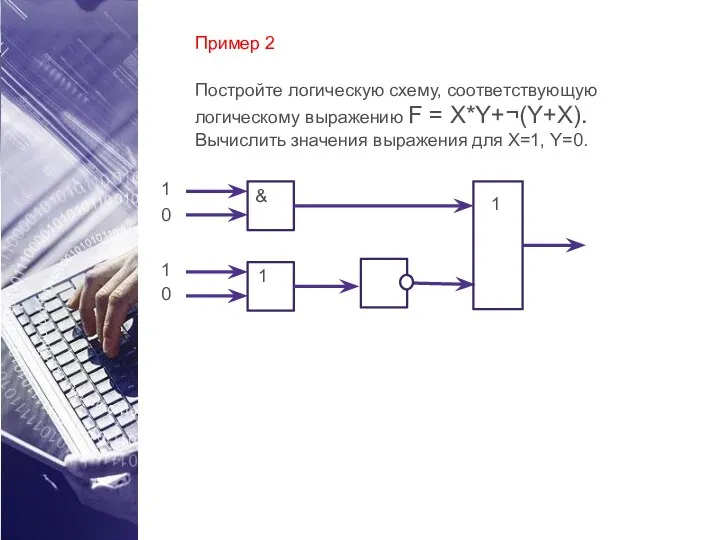
- 40. Пример 2 Постройте логическую схему, соответствующую логическому выражению F = X*Y+¬(Y+X). Вычислить значения выражения для X=1,
- 41. Постройте логические схемы: F = A*(B+C) F = ¬ B*(¬A*B+A) F = D+A*B*C*(¬B+¬C) F = (C*¬A)+¬(A*B+B*C)
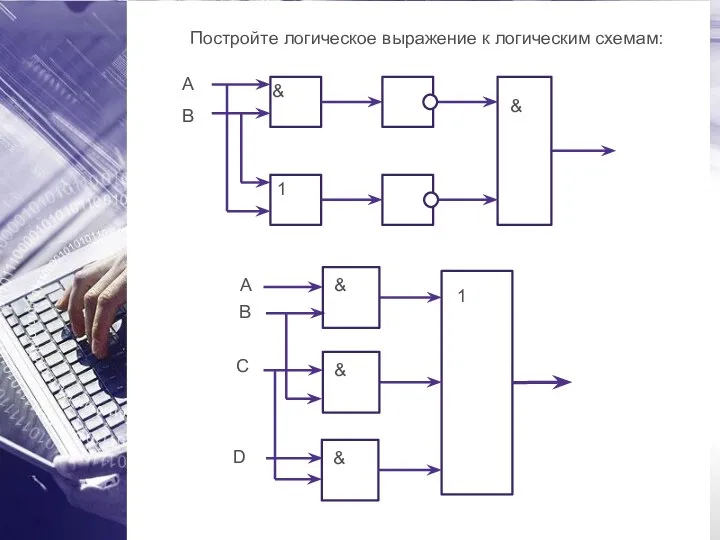
- 42. Постройте логическое выражение к логическим схемам:
- 44. Скачать презентацию

























 Презентация на тему Всемирная паутина
Презентация на тему Всемирная паутина 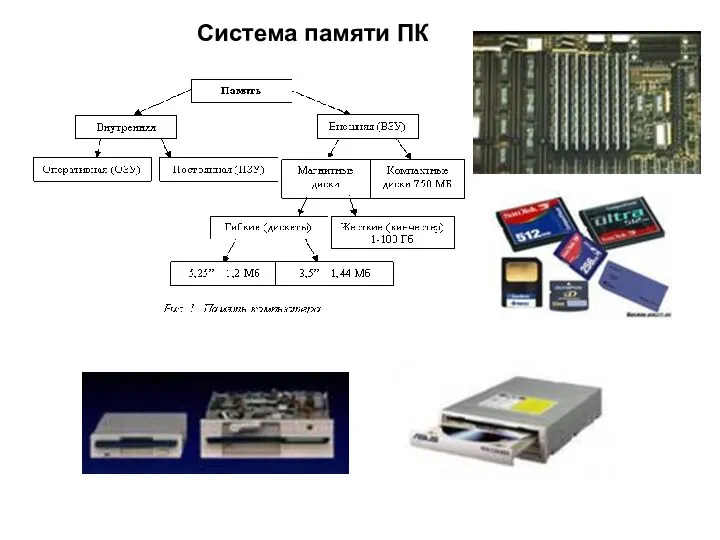 Система памяти ПК
Система памяти ПК Программирование циклических алгоритмов. Начала программирования
Программирование циклических алгоритмов. Начала программирования Конфигурирование операционной системы
Конфигурирование операционной системы Sklearn.impute. Transformers for missing value imputation
Sklearn.impute. Transformers for missing value imputation 16-17_CSS Grid
16-17_CSS Grid Какая бывает информация
Какая бывает информация Разработка игры на Unity
Разработка игры на Unity Спам и защита от него
Спам и защита от него Разработка рекомендация по техническому обслуживанию сетевых серверов
Разработка рекомендация по техническому обслуживанию сетевых серверов Автоматизированная система как объект информационной защиты
Автоматизированная система как объект информационной защиты Создание и развитие систем программирования
Создание и развитие систем программирования Автоматизация и обеспечение информационной безопасности процесса ведения документации и отчетности в ИП Ким С.Г
Автоматизация и обеспечение информационной безопасности процесса ведения документации и отчетности в ИП Ким С.Г Нетикет, или правила хорошего тона в цифровом пространстве – онлайн-конференциях (вебинарах)
Нетикет, или правила хорошего тона в цифровом пространстве – онлайн-конференциях (вебинарах) Комплексный Маркетинг для Вашего Бизнеса. Chat-bot агентство
Комплексный Маркетинг для Вашего Бизнеса. Chat-bot агентство (1 паÑ_а)Тема 2.2. УÑ_ÐовнÑ_й опеÑ_аÑ_оÑ_ _ пÑ_одоÐжение
(1 паÑ_а)Тема 2.2. УÑ_ÐовнÑ_й опеÑ_аÑ_оÑ_ _ пÑ_одоÐжение Образные коды двузначных чисел (урок 11)
Образные коды двузначных чисел (урок 11) Компьютерные технологии в энергомашиностроении
Компьютерные технологии в энергомашиностроении Автоматизация рабочего процесса письменного переводчика в XXI веке
Автоматизация рабочего процесса письменного переводчика в XXI веке Введение в архитектуру ЭВМ
Введение в архитектуру ЭВМ Стандарт электронно-цифровой подписи ГОСТ Р 34.10 различия версий 94 и 12 годов
Стандарт электронно-цифровой подписи ГОСТ Р 34.10 различия версий 94 и 12 годов Компьютерная графика
Компьютерная графика Руслан Тушенцов, известный как Crazy Mega Hell
Руслан Тушенцов, известный как Crazy Mega Hell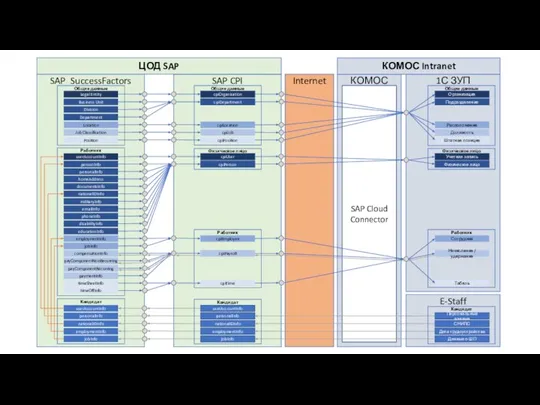 ЦОД SAP Internet
ЦОД SAP Internet Язык программирования Turbo Pascal 7.0
Язык программирования Turbo Pascal 7.0 Разработка информационной системы для технической поддержки ООО Аксус-Самара
Разработка информационной системы для технической поддержки ООО Аксус-Самара Створення системи e-Receipt
Створення системи e-Receipt Qr коды. Задания
Qr коды. Задания