Предмет и содержание медицинской статистики. Лекция 1

5
4
3
2
1
Основные понятия математической статистики
Предмет и содержание медицинской статистики
Основные элементы электронной таблицы.
Выборочные характеристики
ПЛАН ЛЕКЦИИ
Формулы и функции. Операции с формулами

Назначение электронных таблиц
Для представления данных в удобном виде используют таблицы. Компьютер расширяет возможности использования таблиц за счет того, что позволяет не только представлять их в электронной форме, но и обрабатывать входящие в них данные.
Класс программ, используемый для этой цели, называется табличными процессорами, или, проще, электронными таблицами (ЭТ).

Определение ЭТ. Программные средства
Электронные таблицы – это машинные модели обычных таблиц, состоящие из строк и столбцов, обрабатываемые и сохраняемые в памяти компьютера.
Первая программа была разработана в США в 1979 г.
Наиболее популярны такие программы, как Excel, QuattroPro, Lotus 1-2-3, Works

Программные средства ЭТ. VisiCalc
Первая программа для работы с электронными таблицами — табличный процессор, была создана в 1979 году, предназначалась для компьютеров типа Apple II и называлась VisiCalc.

Программные средства ЭТ. Lotus 1-2-3
Lotus 1-2-3 появляется в 1982 году. Предназначался для IBM PC. Lotus объединял в себе вычислительные возможности электронных таблиц, деловую графику и функции реляционной СУБД.

Программные средства ЭТ. QuattroPro

Программные средства ЭТ. Works
Пакет программ MicroSoft Works представляет собой интегрированную среду, включающую в себя текстовый процессор, электронные таблицы, систему управления базами данных и средство коммуникаций (систему компьютерной связи).

Программные средства ЭТ. Microsoft Excel
MS Excel 97
MS Excel 2007
MS Excel 2003
MS Excel 2013

Функции табличных процессоров
создание и редактирование электронных таблиц;
оформление и печать электронных таблиц;
создание многотабличных документов, объединенных формулами;
построение диаграмм, их модификация и решение экономических задач графическими методами;
работа с электронными таблицами как с базами данных: сортировка таблиц, выборка данных по запросам;
создание итоговых и сводных таблиц;
использование при построении таблиц информации из внешних баз данных;
решение экономических задач путем подбора параметров;
решение оптимизационных задач;
статистическая обработка данных.

Основные элементы электронной таблицы.
Документ электронной таблицы называется рабочей книгой.
Рабочая книга представляет собой набор рабочих листов, каждый из которых имеет табличную структуру и может содержать одну или несколько таблиц. В окне документа отображается только текущий рабочий лист активной рабочей книги, с которым и ведется работа.

Основные элементы электронной таблицы.
Каждый рабочий лист имеет название, которое отображается на ярлычке листа, отображаемом в его нижней части. С помощью ярлычков можно переключаться между рабочими листами, входящими в ту же рабочую книгу.
Табличное пространство рабочего листа состоит из строк и столбцов.
Столбцы озаглавлены прописными латинскими буквами и, далее, двухбуквенными комбинациями. Всего рабочий лист может содержать до 16 384 столбцов, пронумерованных от A до XFD.
Строки последовательно нумеруются числами, от 1 до 1 048 576
строка
столбец

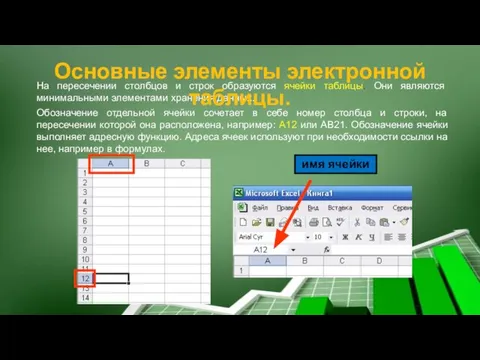
На пересечении столбцов и строк образуются ячейки таблицы. Они являются минимальными элементами хранения данных.
Обозначение отдельной ячейки сочетает в себе номер столбца и строки, на пересечении которой она расположена, например: A12 или AB21. Обозначение ячейки выполняет адресную функцию. Адреса ячеек используют при необходимости ссылки на нее, например в формулах.
имя ячейки
Основные элементы электронной таблицы.

Одна из ячеек всегда активна и выделена рамкой. Эта рамка играет роль курсора. Операции ввода и редактирования всегда осуществляются в активной ячейке.
рамка
маркер автозаполнения

Типы данных в электронных таблицах

Типы данных в электронных таблицах

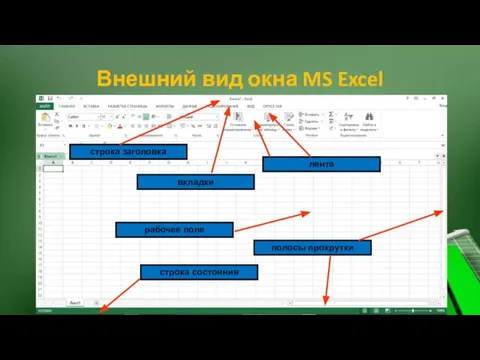
Внешний вид окна MS Excel
строка заголовка
вкладки
лента
рабочее поле
полосы прокрутки
строка состояния

Адресация в Excel
Адресация - это указание на данные находящиеся в определённой ячейке.
Использование адресации облегчает расчёты в таблицах Excel примерно в 2 раза.
АБСОЛЮТНАЯ
ОТНОСИТЕЛЬНАЯ
СМЕШАННАЯ

Адресация в Excel
Относительная - это адресация, при которой формула читается относительно текущего положения ячейки.
=а1*в1 – данную формулу, находящуюся в ячейке С1, ЭВМ для «себя» читает следующим образом: содержимое ячейки, находящейся на два столбца слева в той же строке, перемножить с содержимым ячейки находящейся на один столбец слева в той же строке.
Если эту формулу скопировать из ячейки С1 в ячейку С2, то ее «понимание для ЭВМ» остается точно таким же. Т.е. она возьмет ячейку, находящуюся на 2 столбца слева (а это будет ячейка а2), и перемножит ее с ячейкой находящейся на 1 столбец слева (это будет ячейка в2). Формула в ячейке С2 примет вид =а2*в2
Если эту формулу скопировать в ячейку С3, то она примет вид = а3*в3

Адресация в Excel
Абсолютная – это адресация, при которой идёт указание на конкретную ячейку, адрес которой не изменяется.
$ - признак абсолютной адресации. $ - комбинация кнопок ( Shift + 4 ) в англ. языке.
Знак $ ставится в двух местах - и перед буквой столбца и перед номером строки.

Адресация в Excel
Смешанная – адресация, при которой идёт изменение только одного адреса. Знак $ ставится только в одном месте, или перед буквой столбца или перед номером строки.
При копировании формул:
Относительная - адреса изменяются, относительно текущего положения ячейки.
Абсолютная - адрес не изменяется.
Смешанная - один адрес изменяется, другой нет.

Формулы и функции. Операции с формулами
Возможность использования формул и функций является одним из важнейших свойств программы обработки электронных таблиц. Текст формулы, которая вводится в ячейку таблицы, должен начинаться со знака равенства (=), чтобы программа Excel могла отличить формулу от текста. После знака равенства в ячейку записывается математическое выражение, содержащее аргументы, операции и функции.
В качества аргументов в формуле обычно используются числа и адреса ячеек.

Понятие функции
Для выполнения более сложных вычислений и облегчения многих расчетов используются функции.
Функцией в Microsoft Excel называется сокращенная запись некоторых предопределенных формул, которые выполняют вычисления, используя указанные значения – аргументы.
Например, функция, суммирующая значения ячеек в диапазоне от А2 до А100, будет записываться так: «=СУММ(А2:А100)»

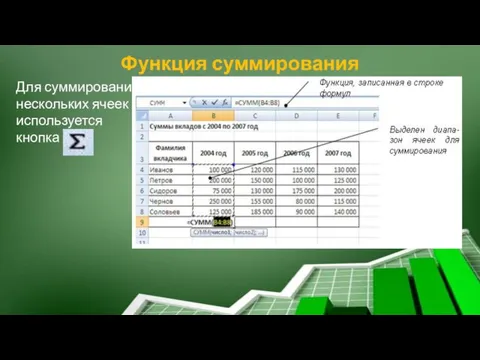
Функция суммирования
Для суммирования нескольких ячеек используется кнопка

Статистические функции
Кроме функции суммирования часто используются функции Среднее (СРЗНАЧ), Минимум (МИН) и Максимум (МАКС), которые относятся к категории Статистических функций.
Для вставки любой из этих функций необходимо из списка кнопки Сумма выбрать название нужной функции:

Использование мастера функций
Для использования других функций, содержащихся в программе Microsoft Excel, можно вызвать диалоговое окно Мастер функций.
В данном окне все функции разбиты по категориям: математические, статистические, финансовые и другие.
Для вызова данного окна требуется из списка кнопки Сумма выбрать команду Другие функции… или щелкнуть на кнопке Вставить функцию в строке формул:

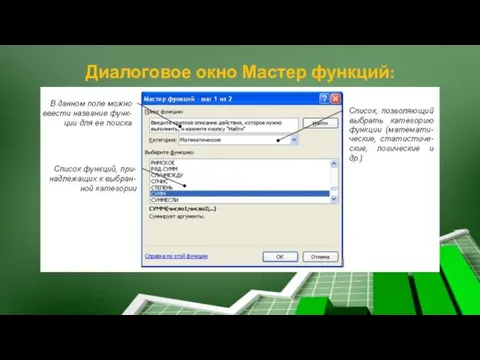
Диалоговое окно Мастер функций:

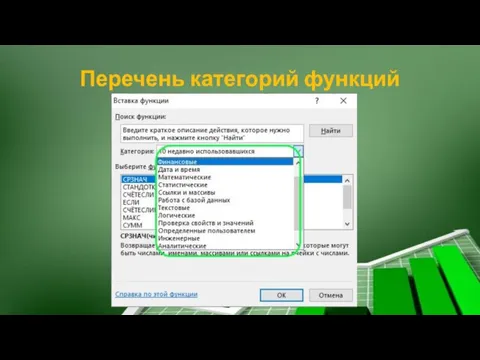
Перечень категорий функций

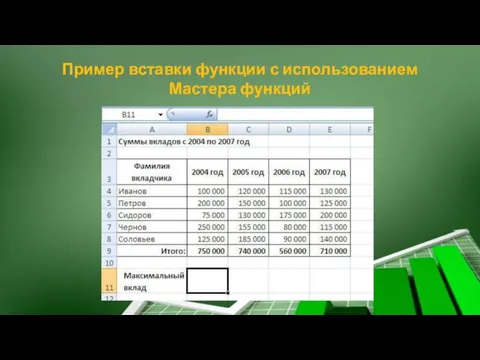
Пример вставки функции с использованием Мастера функций

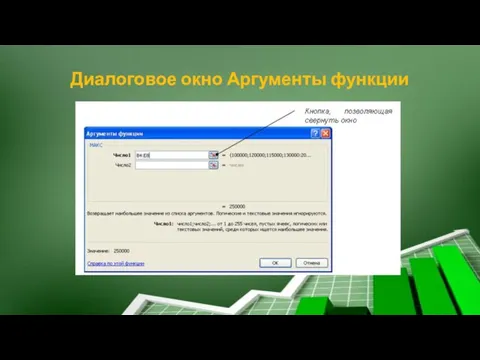
Диалоговое окно Аргументы функции

Предмет и содержание медицинской статистики
В клинических и экспериментальных медицинских исследованиях статистические методы способствуют установлению закономерностей, присущих патологическому процессу, позволяют применять количественные критерии для оценки отдельных видов лечения. Все это требует значительного расширения числа врачей, владеющих статистической методикой в такой степени, чтобы самостоятельно проводить исследования, анализировать медико-статистические данные касающиеся не только здоровья населения, но и показатели, применяемые в педиатрии.
Поэтому знание основ медицинской статистики необходимо врачу независимо от специальности как в практической деятельности, так и в научно-исследовательской работе.

Начало формирования статистики положено зарождением хозяйственного учета и связано с образованием государства. Становление статистики определялось социально-экономическими потребностями общества и государства. Статистический метод формировался постепенно по мере накопления учетных данных, опыта их обработки и анализа. Достижения социально-экономической статистики являются результатом исторического развития. Термин «статистика» (лат. status – положение, состояние явлений). Первым его употребил немецкий ученый Г. Ахенваль в 1749 году.

Прежде чем стать наукой в ее современном понимании статистика прошла многовековую историю развития.
Числовые данные, относящиеся к тем или иным явлениям, начали применяться уже в глубокой древности. Так, известно, что еще за 5 тысяч лет до нашей эры проводился подсчёт населения в Китае, вёлся учет имущества в Древнем Риме, в средние века проводились переписи населения, домашнего имущества, земель.

Статистика – наука, изучающая количественные закономерности материальных
явлений в неразрывной связи с их качественной стороной.
Медицинская статистика - раздел статистики, изучающий состояние здоровья населения и общественное здравоохранение.

Термин “статистика” употребляется в трёх значениях:
Отрасль практической деятельности (“статистический учёт”) по сбору, обработке, анализу и публикации массовых цифровых данных о самых различных явлениях и процессах общественной жизни.
Совокупность цифровых сведений, статистические данные, предоставляемые в отчетности предприятий, организаций, отраслей экономики, а также публикуемые в сборниках, справочниках, периодической прессе, которые являются результатом статистической работы;
Отрасль общественных наук, специальная научная дисциплина, изучаемая в высших и средних специальных учреждениях.

Математическая статистика возникла в XVII веке. Решения первых задач математической статистики содержатся в сочинениях основоположников теории вероятностей Я. Бернулли , П. Лапласа и С. Пуассона.
В математической статистике рассматриваются приближенные методы отыскания законов распределения и числовых характеристик по результатам экспериментов.

В математической статистике разрабатываются теории и методы обработки информации о массовых явлениях.
Исходным материалом статистического исследования являются статистические данные.
Под статистическими данными понимают сведения о числе объектов обширной совокупности признаков.
Например, сведения:
а) о числе отличников в каждом курсе данного факультете;
б) о числе военнообязанных, имеющих рост 2 м, и т. д.

На основании статистических данных часто можно делать вполне определенные научно обоснованные выводы, представляющие большую ценность для науки и практики.
Для этого статистические данные должны быть предварительно определенным образом систематизированы и обработаны.
Методы математической статистики широко применяются в самых различных областях знаний - в физике, астрономии, экономике, геологии, гидрологии, биологии, медицине и др.
Одним из основных методов обработки статистических данных является выборочный метод.

Генеральный совокупность- совокупность всех исследуемых объектов.
Объем выборки - из всей совокупности отбирают случайным образом определенное число объектов.
Например, для контроля качества растворов в ампулах для инъекций на отсутствие в них механических загрязнений из серии 5000 ампул отбирают 150 ампул.
Здесь N=5000 - объем генеральной совокупности
n=150 - объем выборки.

Для того чтобы свойства выборки достаточно хорошо отражали свойства генеральной совокупности, выборка должна быть репрезентативной (представительной).
Согласно закону больших чисел, можно утверждать, что выборка будет репрезентативной, если ее осуществить случайно. Для статистической обработки результаты исследования, представляют в виде числовой выборки: х1, х2, х3,…..,хn.

Вариационный ряд
Выборку, представляющую собой возрастающую последовательность чисел, называют вариационным рядом.
Любую числовую выборку можно записать в виде вариационного ряда.
Например, записав значения выборки
1,10,-2,1,0,1,10,7,-2,10,10,7
в виде возрастающей последовательности, получим вариационный ряд
-2,-2,0,1,1,7,7,10,10,10,10.

Пусть при исследовании некоторой генеральной совокупности получена числовая выборка объема n, причем значение х1 встретилось в выборке n1 раз, значение х2- n2 раз,…, хк - nk раз.
Числа n1,n2,n3,….nк называют частотами,
а их отношения к объему выборки,
n1/n; n2/n;…. nк/n относительными частотами

Очевидно, что сумма частот равна объему выборки n1+n2+n3+……+nк = n,
а сумма относительных частот равна единице,
n1/n + n2/n +……+ nк/n = 1
Статистический ряд
Последовательность пар число с частотой встречаемости (х1;n1),(х2;n2),…..,(хk;nk) называют статистическим рядом.
Обычно статистический ряд записывают в виде таблицы:

Пример. Для выборки
3, 8, -1, 3, 0, 5, 3, -1, 3, 5
1) Определить объем и размах.
2) Записать выборку в виде вариационного ряда и в виде статистического ряда.
Объем выборки n=10, ее размах равен
8-(-1)=9
Записав значения выборки в виде возрастающей последовательности, получим вариационный ряд
-1,-1,0,3,3,3,3,5,5,8.

Статистический ряд можно записать в виде последовательности пар чисел
(-1;2),(0;1),(3;4),(5;2),(8;1)
или в виде таблицы
Для контроля находим сумму частот, которая должна быть равной объему выборки
2+1+4+2+1=10
Для контроля убеждаемся в том, что сумма относительных частот равна единице:
2/10+1/10+4/10+2/10+1/10=1

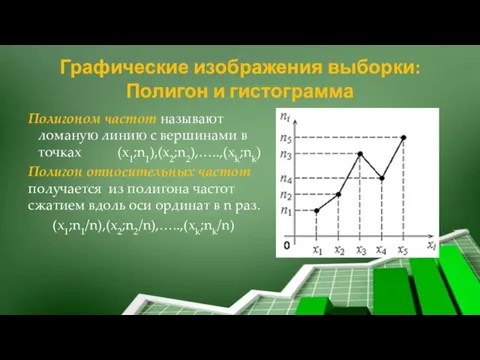
Графические изображения выборки:
Полигон и гистограмма
Полигоном частот называют ломаную линию с вершинами в точках (х1;n1),(х2;n2),…..,(хk;nk)
Полигон относительных частот получается из полигона частот сжатием вдоль оси ординат в n раз.
(х1;n1/n),(х2;n2/n),…..,(хk;nk/n)

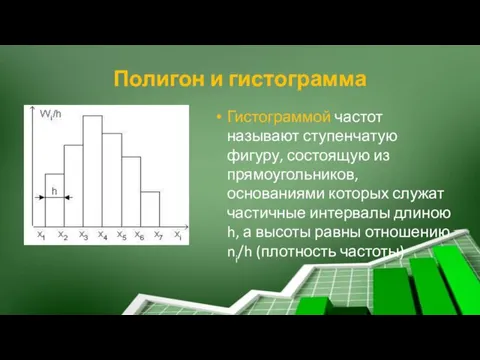
Полигон и гистограмма
Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению ni/h (плотность частоты)

Выборочные характеристики
Среднее арифметическое значение.
Пусть имеется некоторая выборка объема n:
x1, x2, ……, xn.
Сумма объема выборки определяется с помощью формулы
S = x1+x2+……+xn
Выборочное среднее для вариационного ряда определяется формулой
Mв = (x1+ x2 +…..+ xn)/n
∑ xi
Мв = ---------
n

Среднее квадратичное отклонение
Этот показатель характеризует степень разброса результатов наблюдений вокруг средней арифметической величины, а также дает сведения об устойчивости и не устойчивости изучаемого процесса.
Для вариационного ряда среднее квадратичное отклонение вычисляется по формуле
σв= ((x1-M)2 + (x2-M)2+ ……+(xn-M)2)/(n-1)
∑(xi-M)2
σв= -------------- , i = 1,n
n – 1

Для статистического ряда среднее квадратичное отклонение вычисляется по формуле
σст= (n1(x1- M)2 +n2(x2-M)2+ …+nk(xk-M)2)/(n-1)
∑ni (xi-M)2
σcт = --------------- , i = 1,k
n – 1

Стандартная ошибка
При выборке малого объема, оценка арифметического значения может значительно отличаться от истинного значения случайной величины и приводить к грубым ошибкам.
Поэтому при небольшом объеме наблюдений используются интервальные оценки, которые определяются двумя числами - концами интервала, покрывающего оцениваемую случайной величиной.

Стандартная ошибка
среднего арифметического вычисляется по формуле
m = σ / n
Доверительный интервал (M ± m)
Величина стандартная ошибка, показывает те пределы в которых заключается истинное значение случайной величины
M ± m.
А) Верхний предел M + m
Б) Нижний предел M - m

Показатель точности результатов
(Критерий достоверности)
С помощью среднего арифметического значения М и средней квадратичное ошибки m, можно оценить точности производимых наблюдений.
Для этого вычисляется показатель точности наблюдений, который обозначим Rt.
Rt = m / M * 100%

Если R<=5% , то тогда 95% результатов исследований считается достоверными.
( Вероятность и доверительный интервал результатов исследования, подчиняющихся нормальному закону распределения
P= 95%( M+σ), P=99%( M+2σ), P=99,9 ( M+3σ)).

где, Т - критерий Стъюдента;
М1 - среднее арифметическое значение результата наблюдений группы контрольных опытов;
М2 - среднее арифметическое значение результата других групп наблюдений;
m1 , m2 - стандартные ошибки контрольных и наблюдаемых групп;

Далее на основании вычисленных значений Tэксп и числа k - степень свободы, по таблице Стъюдента определяется вероятность различий.
При сравнении двух групп (рядов) степень свободы вычисляется по формуле
k = n1 + n2 - 2
n1 - число наблюдений в контрольных группах (опытах).
n2 - число наблюдений в других группах (опытах).

Критерий Фишера
Для проверки гипотезы о равенстве основных дисперсий сумм (σ12=σ22) вычисление критерия Стъюдента при нормальном распределении может быть недостаточным, особенно, при малых числах измерений. Было предложено рассмотреть отношение дисперсий и обозначить буквой F:

Развитие корреляционного и регрессионного анализа
Начало корреляционного и регрессионного анализа относится ко второй половине ХIХ века и связано с именем двоюродного брата Ч. Дарвина – Френсисом Гальтоном (1822–1911). Он ввел понятие «закона регрессии», связав его со средним снижением роста сыновей по сравнению с ростом отцов (1899 г). Ему же принадлежит введение числовой меры, оценивающей силу связи показателей (корреляцию). Поэтому началом разработки корреляционно-регрессионного анализа ученые–статистики считают статью Ф. Гальтона «Регрессия, наследственность и панмиксия» (1896 г), в которой автор «дал определение корреляции, построил теоретическую модель совместного измерения двух переменных, ввел понятие линии регрессии и корреляционного индекса «r».

В развитии методов корреляционного и регрессионного анализа особо следует отметить заслуги таких ученых, как К- Пирсон, X. Спирмэн, А. Бравэ, Г. У. Юл, А. А. Чупров, С. М. Бартлет, М. Г. Кендэл, С. Коллер, М. Езекиэл и многих других.

В медико - биологических исследованиях большое внимание уделяется установлению связей между различными параметрами, признаками или явлениями.
1.Причинно-следственная связь
Причинно-следственные отношения – это связь явлений и процессов, когда изменение одного и них – причины – ведет к изменению другого – следствия.
Виды связей

Между различными явлениями и их признаками необходимо прежде всего выделить 2 типа связей: функциональную (жестко детерминированную) и статистическую (стохастически детерминированную).
Стахостическая связь – это связь между величинами, при которой одна из них, случайная величина у, реагирует на изменение другой величины х или других величин х1,х2 …хn (случайных или неслучайных) изменением закона распределения.
2.Функциональные и стохастические связи

Однако в медико - биологических экспериментах функциональные зависимости встречаются далеко не всегда, а чаще одному значению признака соответствует несколько значений другого признака.
Например, при одном и том же росте, вес различных индивидуумов может быть различен.
[3]

Корреляционный анализ
Раздел математической статистики, занимающейся установлением взаимосвязей между случайными величинами, называется корреляционно - регрессионным анализом.
С помощью корреляционного анализа определяется теснота и направление связи между признаками.
Установление взаимосвязи между различными признаками и показателями функционирования организма, позволяют по изменениям одних из них, судить о состоянии других.

Пусть в результате медико - биологических исследований получены экспериментальные данные изменения двух показателей X и Y.
X: x1 ; x2 ; ……; xn
Y: y1 ; y2 ; ……; yn
Если полученные данные нанести на плоскость координат, то точки займут определенную область, которую обычно называют корреляционным полем.

Наиболее часто в экспериментальных исследованиях используется линейная корреляционная зависимость.
При этом подразумевается, что генеральные совокупности для X и Y имеют нормальный закон распределения или близкий к нему.
В этом случае определение тесноты линейной связи производится по формуле:
где r - коэффициент корреляции σx и σy - средние квадратичное отклонения величин X и Y

Коэффициент корреляции лежит в пределах от -1 до +1 (-1<= Rx/y <= +1):
1) Отрицательные значения R от 0 до -1
указывают на обратную зависимость между переменными.
2) Положительные значения R от 0 до +1 характеризуют прямую связь между признаками.
3) Когда R=0, это говорит об отсутствии статистической линейной взаимосвязи между признаками.
[3]

МОДЕЛИРОВАНИЕ
Моделирование - это метод исследования, при котором объект исследования заменяется другим, который называется моделью.
В настоящее время существуют самые разнообразные типы моделей, которые можно классифицировать различными способами.
В соответствии с этим все модели, используемые в биологии и медицине, подразделяются на биологические, физико-химические, кибернетические, математические.

Физические модели
Физические (аналоговые) модели - это физические системы или устройства, которые путем специального конструирования имитируют реальный объект.
К физическим моделям относятся электромеханические устройства, заменяющие органы и системы живого организма:
- аппарат искусственного дыхания (моделируют легкое),
- аппарат искусственного кровообращения (модель сердца),
- аппарат гемодиализа (модель почки) и т.д.
В настоящее время, эти аппараты достаточно широко используется в лечебной практике.

Математические модели
Это совокупность уравнений, устанавливающих количественную зависимость между параметрами, которые описывают свойства изучаемого объекта, явления или процесса.
Особенности математических моделей:
- математическая модель позволяет судить о поведении объекта в таких условиях, которые трудно создать в эксперименте или клинике;
- математическая модель позволяет прогнозировать течение болезни и подобрать оптимальные варианты лечения;
- математическая модель биологических систем, позволяет уменьшить время исследования и сократить число животных, необходимых для исследования.

Регрессионный анализ
Функция, позволяющая по величине одного признака -Х, находить средние значения другого признака -Yх, называется регрессией.
Регрессионный анализ позволяет описать форму зависимости между случайными переменными с помощью уравнений регрессии (линейных, квадратичных, показательных и т. д.).
Регрессионный и корреляционный анализы тесно связаны между собой.
Аналитической формы записи связи между значениями Х и У является уравнением линии регрессии.
Линия регрессии проводится в корреляционном поле так, чтобы она проходила наиболее близко ко всем точкам.

В качестве критерия близости обычно используется - МНК «метод наименьших квадратов».
МНК- минимум суммы квадратов отклонения экспериментальных точек от линии регрессии. ∑ (Y экс - Yтеор )2 => min (i=1,n).

Рассмотрим линейную регрессию, которая выражается простым уравнением линейной зависимости:
Здесь, Yx- средняя арифметическая значение переменной Y, соответствующее заданному значению Х; a и b - параметры уравнения;
b- свободный член, a- коэффициент регрессии.
Вычисленные по этим формулам параметры уравнения регрессии определяют «наилучшую» прямую Yтеор, т.е. сумма квадратов разностей между наблюдаемыми оцененными значениями Уэксп будут минимальны (min).

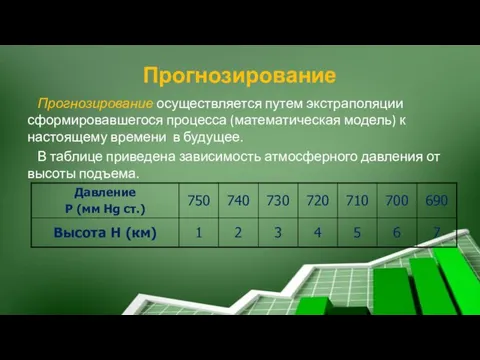
Прогнозирование
Прогнозирование осуществляется путем экстраполяции сформировавшегося процесса (математическая модель) к настоящему времени в будущее.
В таблице приведена зависимость атмосферного давления от высоты подъема.

На основании этих данных строится математическая модель в виде уравнении регрессии y=ax+b, которая полностью описывает эту таблицу. На основе полученной математической модели определяется атмосферное давление Yпрогн на высоте Хпрогноз .
В формулу Y =-10x+760 в место х ставится Хпрогноз (прогнозируемая высота) и определяем прогнозируемую величину давления Yпрогн .