Логические основы компьютера

Слово «Логика» происходит от древнегреческого «logos», что означает мысль, закон, рассуждения, наука.
Логика – наука о законах мышления. Но логика изучает не только правильное, но и «неправильное» мышление: логические ошибки, противоречия, парадоксы, софизмы и парологизмы.

Первые учения о формах и способах рассуждений возникли в странах Древнего востока (Китай, Индия), но в основе современной логики лежат учения, созданные древнегреческими мыслителями.
Основы формальной логики заложил Аристотель, который впервые отделил логические формы мышления от его содержания.
Над возможностями применения логики в технике ученые и инженеры задумывались уже давно. Например, голландский физик Пауль Эренфест (1880-1933) писал еще в 1910 году:

«… Пусть имеется проект схемы проводов автоматической телефонной станции. надо определить:
1)будет ли она правильно функционировать при любой комбинации, могущей встретиться в ходе деятельности станции;
2) не содержит ли она излишних усложнений.
Каждая такая комбинация является посылкой, каждый маленький коммутатор есть логическое «или-или»… Правда ли, что несмотря на существование алгебры логики, своего рода «алгебра распределительных схем» должна считаться утопией?».
Созданная позднее М.А.Гавриловым (1903 – 1979) теория релейно-контактных схем показала, что это вовсе не утопия.

Законы логики отражают в сознании человека свойства, связи и отношения объектов окружающего мира.
Основными формами мышления являются понятие, высказывание, умозаключение.

Логическое высказывание- это любое повествовательное предложение, в отношении которого можно сказать, истинно оно или ложно.
В Булевой алгебре высказывания рассматриваются не по содержанию и не по смыслу, а только в отношении того истинно оно или ложно. Принято обозначать: истинно — 1, а ложно — 0.

Примеры логических высказываний:
«снег холодный»- данное предложение является высказыванием и при том истинным.
«Снег теплый» — высказывание, но ложно.
«Речка движется и не движется» не является высказыванием, так как из этого предложения нельзя понять истинно оно или ложно.
«Который час?» — это не высказывание, а вопросительная фраза.

Из данных предложений выберите те, которые являются высказываниями
Коля спросил: «Который час?»
Картины Пикассо слишком абстрактны.
Каникулы!
Решение задачи- информационный процесс.
Число 2 является делителем числа 7 в некоторой системе счисления

Простейшее высказывание, связанное между собой союзами: «И», «ИЛИ», «НЕ» — составляют составное высказывание, истинность или ложность, которого можно вычислить.
А -«Тимур поедет летом на море»
В -«Тимур летом отправится в горы».
Простые высказывания
A и B
А или В
если A, то B
не A и B
A тогда и только
тогда, когда B
Тимур поедет летом на море и отправиться в горы.
Тимур не поедет летом на море и отправиться в горы.
Тимур поедет летом на море или отправиться в горы.
Тимур поедет летом на море тогда и только тогда, когда отправиться в горы.
Если Тимур поедет летом на море, то отправиться в горы.

Логические операции
Логическая операция может быть описана таблицей истинности указывающей, какие значения принимает сложное высказывание при всех возможных значениях простых высказываний

Конъюнкция —
логическое умножение
Союз «И».
Обозначение: Λ, Χ, ·, &, and
«Сегодня солнечный день, и Остап пошел купаться»

Дизъюнкция —
логическое сложение
Союз «ИЛИ».
Обозначение: V, +, or
«Колумб был в Индии или в Египте»

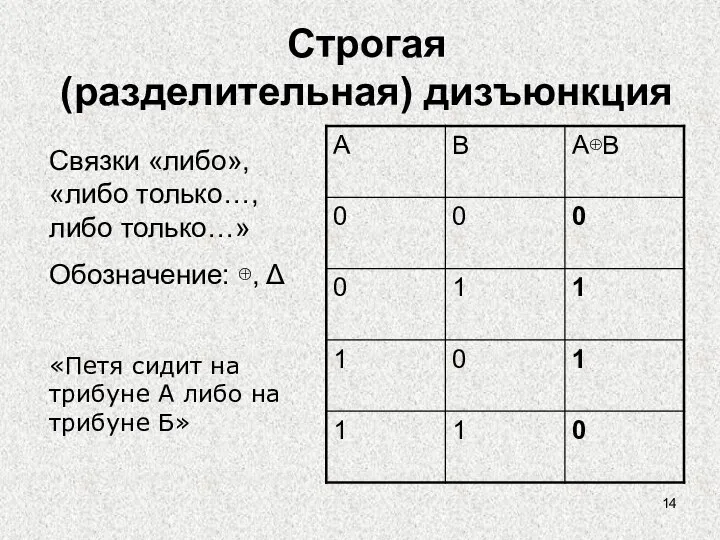
Строгая
(разделительная) дизъюнкция
Связки «либо», «либо только…, либо только…»
Обозначение: ⊕, Δ
«Петя сидит на трибуне А либо на трибуне Б»

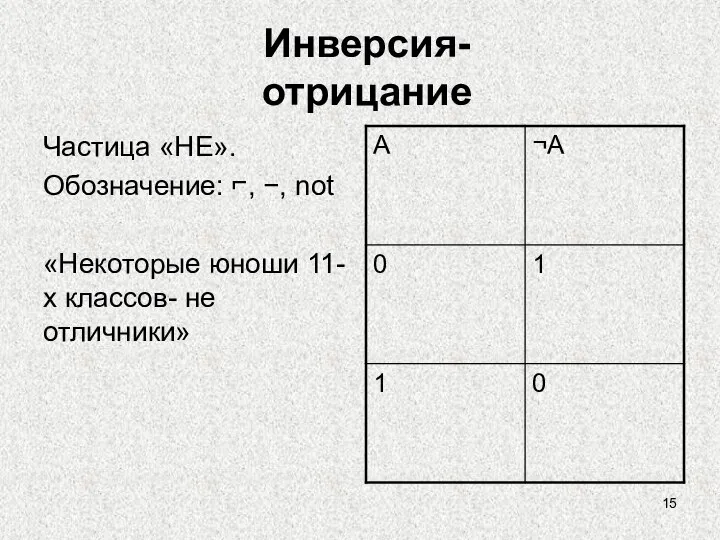
Инверсия-
отрицание
Частица «НЕ».
Обозначение: ⌐, −, not
«Некоторые юноши 11-х классов- не отличники»

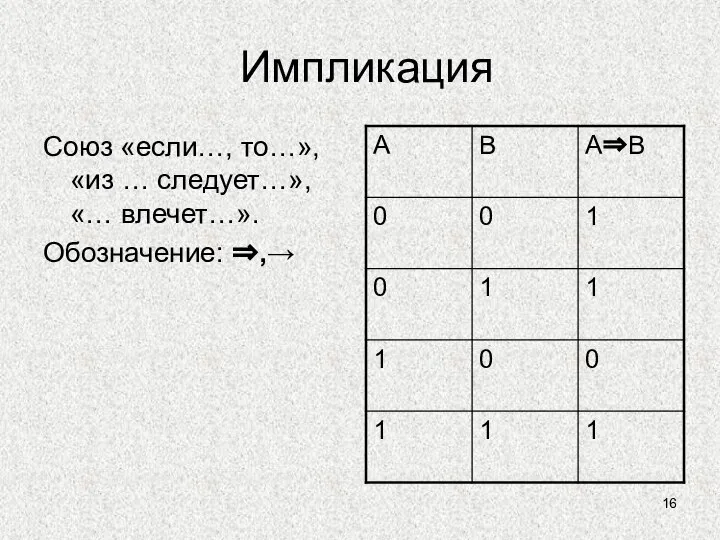
Импликация
Союз «если…, то…», «из … следует…», «… влечет…».
Обозначение: ⇒,→

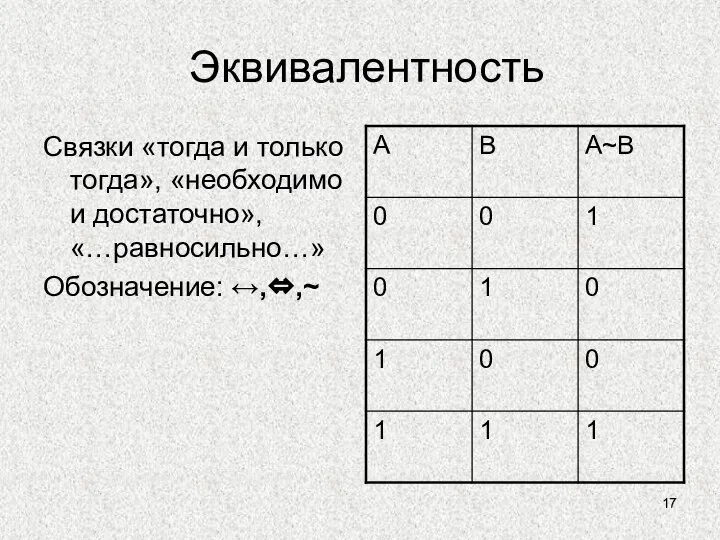
Эквивалентность
Связки «тогда и только тогда», «необходимо и достаточно», «…равносильно…»
Обозначение: ↔,⇔,~

Диаграммы Эйлера
Конъюнкция — логическое умножение

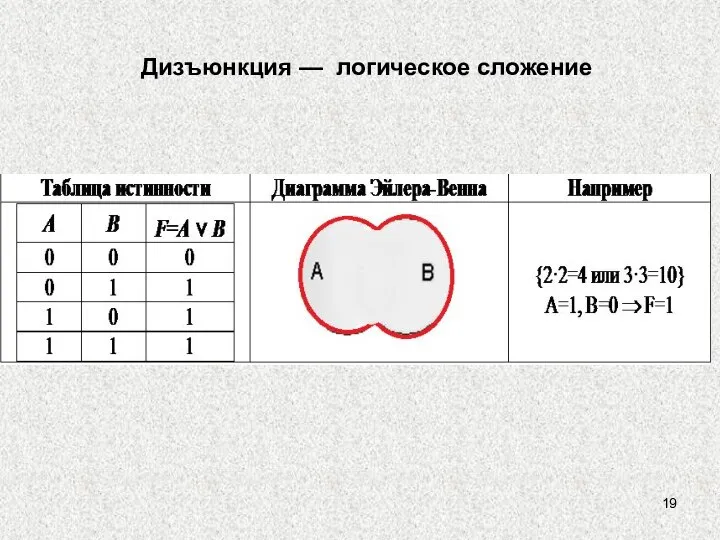
Дизъюнкция — логическое сложение

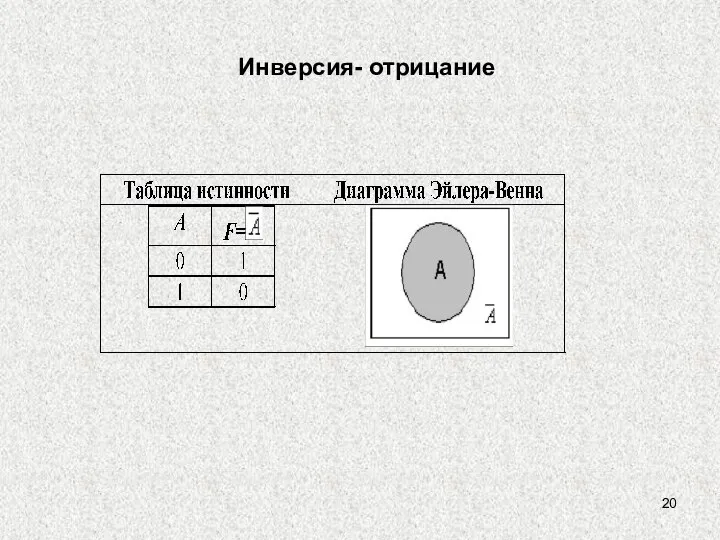
Инверсия- отрицание

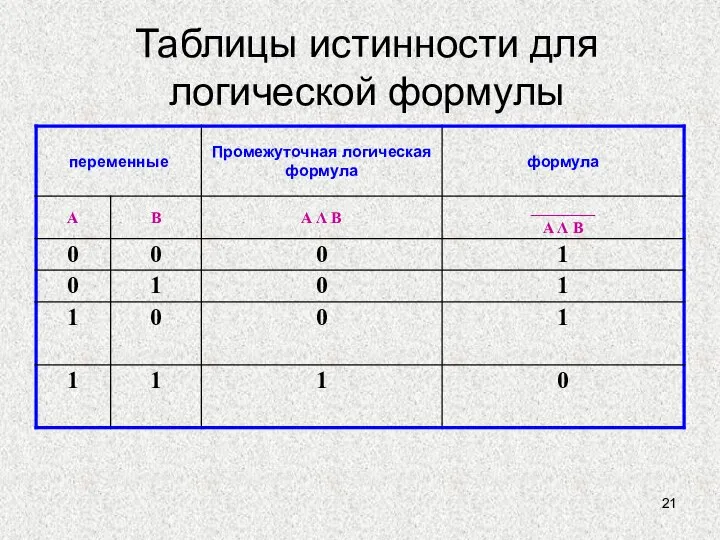
Таблицы истинности для логической формулы