Архитектура вычислительных систем. Раздел 2. Информация, кодирование и обработка в ЭВМ

Определение и классификация информации
Определений информации:
• отрицание энтропии (Л. Бриллюэн);
• мера сложности структур (Моль);
• отраженное разнообразие (Урсул);
• содержание процесса отражения (Тузов);
• вероятность выбора (Яглом);
• снятая неопределенность наших знаний о чем-то (К. Шеннон);
• обозначение содержания, полученного из внешнего мира в
процессе нашего приспособления к нему и приспособления
к нему наших чувств (Н. Винер).

Информация — это осознанные сведения об окружающем мире.

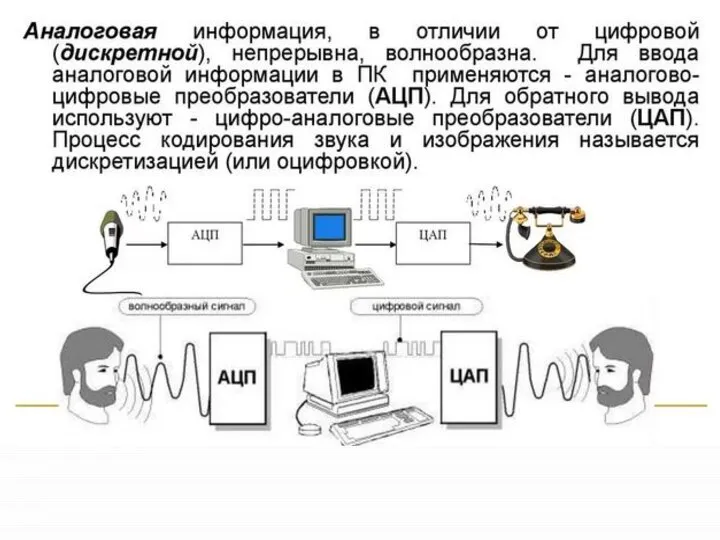
Аналоговая информация
Исторически первой технологической формой получения, передачи, хранения информации являлось
а н а л о г о в о е (непрерывное) представление звукового, оптического, электрического или другого сигнала (сообщения).
Магнитная аудио- и видеозапись, фотографирование, запись на виниловые грампластинки, проводное и радиовещание — основные способы хранения и передачи информации в аналоговой форме.

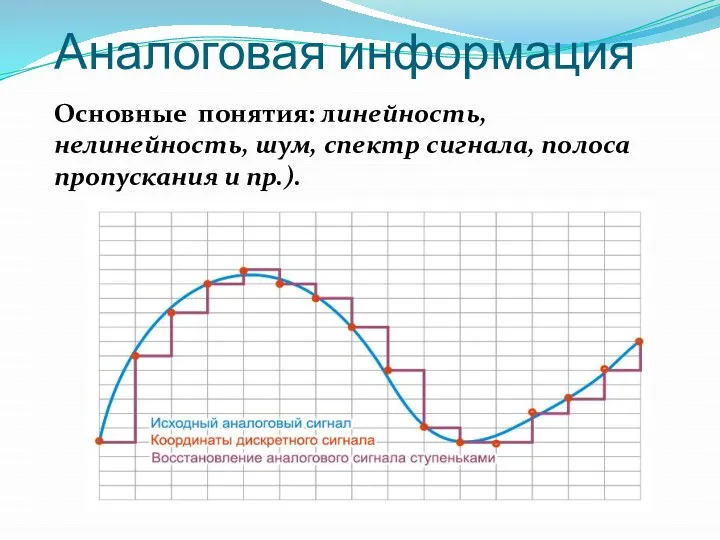
Аналоговая информация
Основные понятия: линейность, нелинейность, шум, спектр сигнала, полоса пропускания и пр.).

Аналоговая информация
Аналого-цифровые (АЦП или дискретные) преобразователи чаще всего изготавливаются в виде интегральных схем.
В необходимых случаях осуществляется обратное — дискретно-аналоговое или цифроаналоговое преобразование — ЦАП (digital-to-analog conversion — DAC).

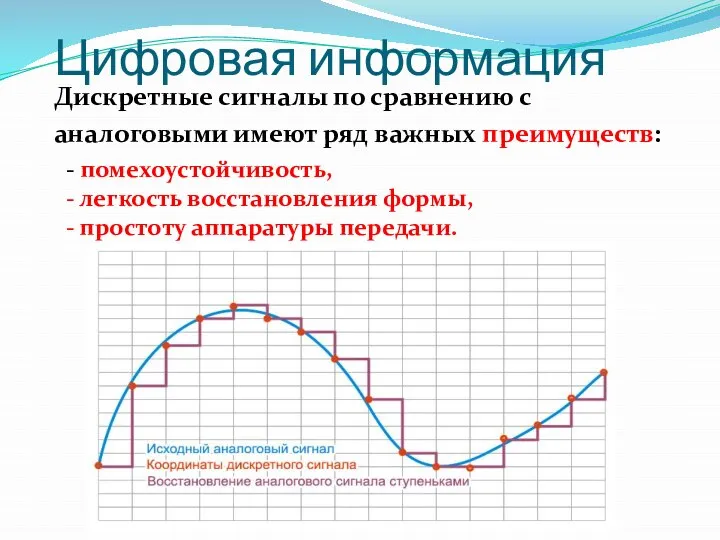
Цифровая информация
Дискретные сигналы по сравнению с
аналоговыми имеют ряд важных преимуществ:
- помехоустойчивость,
- легкость восстановления формы,
- простоту аппаратуры передачи.

Какой вид информации?

Цифровая информация
Сигналы представляют собой дискретные электрические или световые импульсы. При таком способе вся емкость коммуникационного канала используется для передачи одного сигнала. Цифровой сигнал использует всю полосу пропускания кабеля.
Полоса пропускания
- это разница между максимальной и минимальной частотой, которая может быть передана по кабелю. Каждое устройство в таких сетях посылает данные в обоих направлениях, а некоторые могут одновременно принимать и передавать.

Дискретный цифровой сигнал сложнее передавать на большие расстояния, чем аналоговый сигнал, поэтому его предварительно модулируют на стороне передатчика, и демодулируют на стороне приёмника информации.
Использование в цифровых системах алгоритмов проверки и восстановления цифровой информации позволяет существенно увеличить надёжность передачи информации.

Модуля́ция (лат. modulatio — размеренность, ритмичность) — процесс изменения одного или нескольких параметров высокочастотного несущего колебания по закону низкочастотного информационного сигнала.

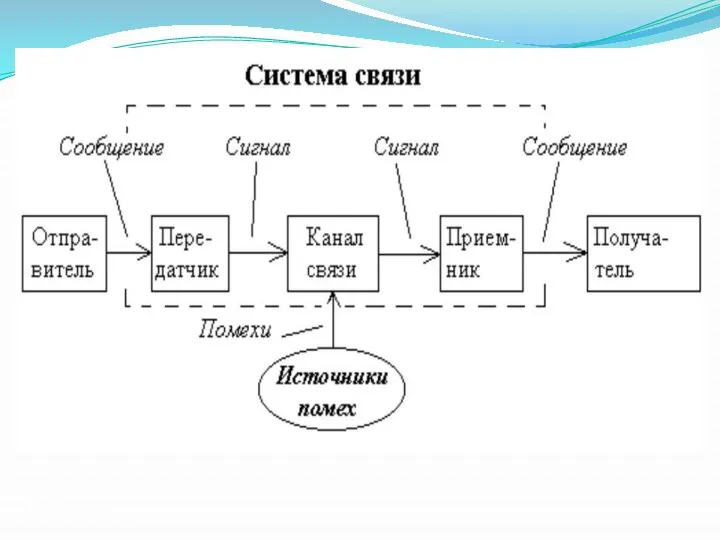
ПЕРЕДАЧА ДАННЫХ
Передача данных — процесс переноса информации в виде сигналов от точки к точке или от точки к нескольким точкам средствами электросвязи по каналу передачи данных.

При обмене данными по каналам используется три метода передачи данных:
Канал передачи —
• симплексная (однонаправленная) передача (телевидение,
радио);
• полудуплексная (прием и передача информации осуществляются поочередно);
• дуплексная (двунаправленная), каждая станция одновременно передает и принимает данные.
это комплекс технических средств и среды распространения, обеспечивающий передачу сигнала.

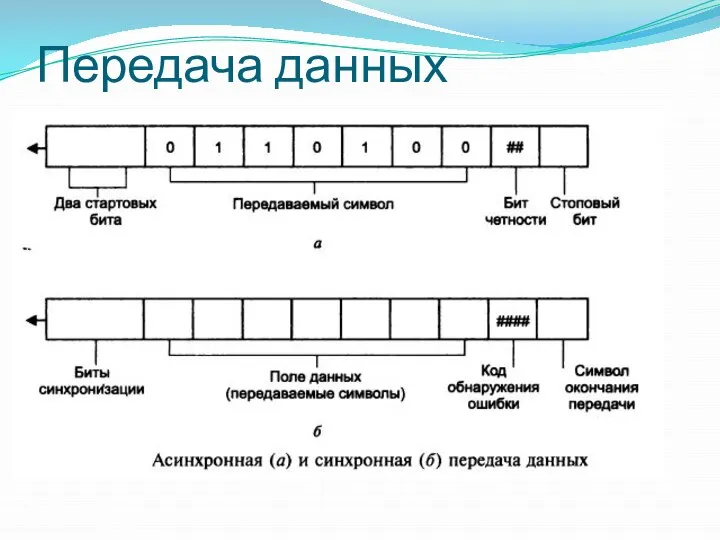
Широко используются следующие методы последовательной передачи — асинхронная и синхронная .
При асинхронной передаче каждый символ передается отдельной посылкой. При синхронной передачи символы группируются.

Стартовые биты предупреждают приемник о начале передачи. Затем передается символ.
Для определения достоверности передачи используется бит четности (бит четности равен 1, если количество единиц в символе нечетно, и 0 — в противном случае.
Последний бит («стоп-бит») сигнализирует об окончании передачи.

Передача данных

Передача данных
При использовании синхронного метода данные передаются блоками.
Для согласования работы приемника и передатчика в начале блока передаются биты синхронизации. Затем передаются данные, код обнаружения ошибки и символ окончания передачи.
При синхронной передаче данные могут передаваться и как символы, и как поток битов. В качестве кода обнаружения ошибки обычно используется код CRC.

Контрольные вопросы
Что такое информация?
Что такое передача информации?
По чему происходит передача информации?
Какие методы передачи информации существуют?
Что применяется для обеспечения корректности передачи информации?
Для чего применяются стартовые биты?

Измерение количества информации
Информацию, содержащуюся в сообщении, можно трактовать в смысле ее новизны или, иначе, уменьшения неопределенности знаний «приемника информации» об объекте.
В качестве единицы информации Клод Шеннон предложил принять один бит (от англ. bit — binary digit — двоичная цифра).
(1916-2001)

Клод Шенон
Американский инженер, криптоаналитик и математик.
Считается «отцом информационного века». Является основателем теории информации, нашедшей применение в современных высокотехнологических системах связи.

Предоставил фундаментальные понятия, идеи и их математические формулировки, которые в настоящее время формируют основу для современных коммуникационных технологий.
В 1948 году предложил использовать слово «бит» для обозначения наименьшей единицы информации.
Кроме того, понятие энтропии было важной особенностью теории Шеннона
Магистерскую диссертацию Шеннона по электротехнике Массачусетского технологического института «Символический анализ релейных и переключательных схем» назвали самой важной в 20-м веке.

Бит — слишком мелкая единица измерения, на практике чаще применяется более крупная единица — б а й т, равная восьми битам.
В частности, восемь бит требуется для того, чтобы закодировать любой из 256 символов ASCII (256 = 2^8).
Часто возникает неоднозначность в интерпретации, например, 1 Мбайта, который может рассматриваться как 1000 Кбайт (десятичный мегабайт), так и 1024 Кбайт (бинарный мегабайт).

Кодирование символьной информации
Код (code) —
Рассмотрим методы дискретного представления информации, или кодирования (которые, надо сказать, появились задолго до вычислительных машин).
Широко известным примером является азбука Морзе в которой буквы латиницы (или кириллицы) и цифры кодируются сочетаниями из «точек» и «тире».
набор знаков, символов и правил представления информации.

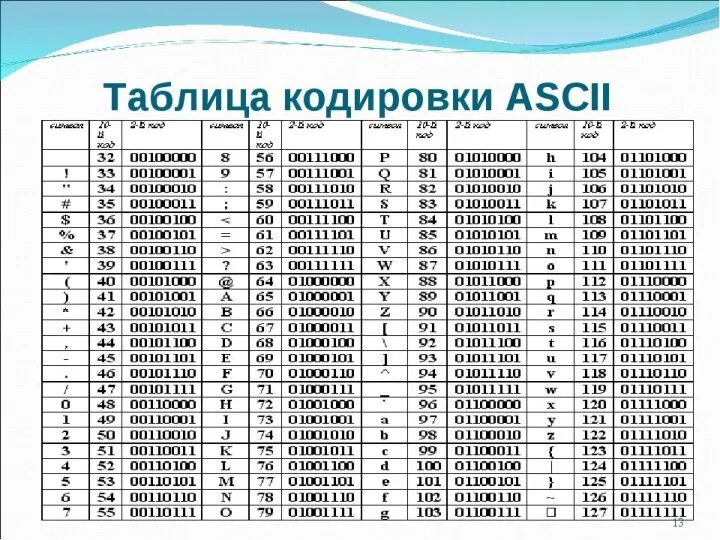
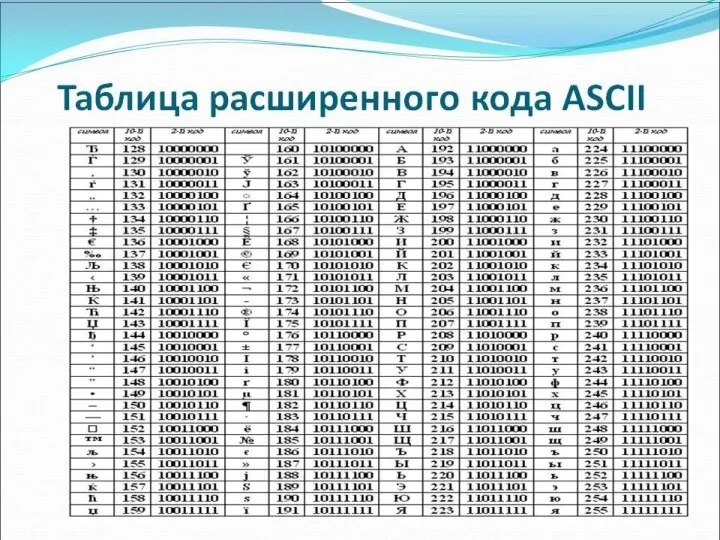
ASCII и UTF-8
ASCII — American Standard Code for Information Interchange.
ASCII была разработана (1963 год) для кодирования символов. ASCII использует для кодирование 8-ми бит. Значит ей можно закодировать 256 символов.
Кодировка символов часто называется кодовой страницей.
На смену ей пришла кодировка UTF-8 (Unicode Transformation Format).
В Unicode используются 16-битовые (2-байтовые) коды, что позволяет представить 65536 символов.

Избыточные коды
При записи и передаче данных часто используются избыточные коды, т. е. такие, которые за счет усложнения структуры позволяют повысить надежность передачи данных.
Коды с обнаружением ошибок.
Распространенным методом обнаружения ошибок является к о н т р о л ь п о ч е т н о с т и .

При записи байта информации в запоминающее устройство генерируется дополнительный контрольный бит, в который записывается «0», если это число четное, и «1», если оно нечетное. Если при чтении ранее записанного байта вновь получить контрольный бит и сравнить его с уже имеющимся, то можно судить о достоверности получаемой информации.

Избыточные коды
При записи и передаче данных часто используются избыточные коды, т. е. такие, которые за счет усложнения структуры позволяют повысить надежность передачи данных.

Коды с обнаружением ошибок
Распространенным методом обнаружения ошибок является к о н т р о л ь по четности.
В этом случае при записи байта информации в запоминающее устройство генерируется дополнительный контрольный бит, в который записывается «О», если это число четное, и «1», если оно нечетное.
Если при чтении ранее записанного байта вновь получить контрольный бит и сравнить его с уже имеющимся, то можно судить о достоверности получаемой информации.

Избыточные коды
Широко используется для обнаружения ошибок в блоках данных также код с циклическим контролем — циклический избыточный код обнаружения ошибок (Cyclic Redundance Check — CRC).
Вычисляется контрольная сумма содержимого блока данных перед его передачей, включается в одно из полей блока, а затем повторно вычисляется после передачи. Несовпадение результатов свидетельствует об ошибке в передаваемом содержимом.

Корректирующие коды
В ответственных приложениях, требующих повышенной надежности хранения информации, применяются более серьезные, чем контроль четности, методы обеспечения целостности данных. К ним относятся корректирующие коды (Error Correction Code — ЕСС), позволяющие не только обнаруживать ошибки, но и восстанавливать искаженную информацию за счет ее избыточности.

Системы счисления
Позиционные и непозиционные системы счисления.
Системой счисления называется совокупность приемов и правил для записи чисел цифровыми знаками.

Непозиционные Системы счисления
Непозиционная система счисления – система, для которой значение символа не зависит от его положения в числе.
Для их образования используют в основном операции сложения и вычитания.
Примером непозиционной системы счисления является римская система, использующая набор следующих символов: I, V, X, L, C, D, M и т. д.

Позиционная система счисления
Позиционная система счисления – система, в которой значение символа определяется его положением в числе: один и тот же знак принимает различное значение.
Любая позиционная система характеризуется основанием.
Основание (базис) позиционной системы счисления – количество знаков или символов, используемых для изображения числа в данной системе.

Основание позиционной системы счисления — количество (Р) различных цифр, используемых для изображения числа в позиционной системе счисления.
Значения цифр лежат в пределах от 0 до Р - 1.
m – количество разрядов.

Пример
В двоичной системе (q=2)
11010.1012 = 1 · 24 + 1 · 23 + 0 · 22 + 1 · 21 + 0 · 20 + 1 · 2-1 + 0 · 2-2 + 1 · 2-3;
в) в шестнадцатиричной системе (q=16)
A3F.1CD16 = A · 162 + 3 · 161 + F · 160 + 1 · 16-1 + C · 16-2 + D · 16-3.

Контрольные вопросы:
Что обеспечивает система счисления?
Какая система счисления называется позиционной?
Какая система счисления называется непозиционной?
Какое равенство отожествляется с позиционной системой счисления?
Приведите примеры позиционных и непозиционных систем счисления.

Недесятичная арифметика и её правила
Двоичная арифметика
Арифметические операции во всех позиционных системах счисления выполняются по одним и тем же хорошо известным вам правилам.

Сложение
Правила двоичного сложения:
0+0=0
0+1=1
1+0=1
1+1=10

Пример
1102
+
112
10012
Проверим правильность вычислений сложением в десятичной системе счисления. Переведем двоичные числа в десятичную систему счисления и затем их сложим:
1102=1*22 + 1*21+ 0*20 = 610;
112 = 1*21 + 1*20 = 310;
610 + 310 = 910.
Теперь переведем результат двоичного сложения в десятичное число:
10012 = 1*23 +0*22 + 0*21 + 1*20 = 910

Вычитание
Правила двоичного вычитания:
0 - 0 = 0
0 - 1 = 11 1 - 0 = 1
1 - 1 = 0

Пример
1102 - 112:
1102
112
112
--

Умножение
Правила двоичного умножения:
0 * 0 = 0
0 * 1 = 0
1 * 0 = 0
1 * 1 = 1

Пример
1102
112___
110
110 100102
+
x

Деление
Деление. Операция деления выполняется по алгоритму, подобному алгоритму выполнения операции деления в десятичной системе счисления. В качестве примера произведем деление двоичного числа 1102 и 112:
1102 |__112___
- | 102
11
0

Контрольные вопросы:
Какая арифметика называется недесятичной?
Как производится сложение, вычитание, умножение, и деление в двоичной системе счисления?
Как производится сложение, вычитание, умножение, и деление в восьмеричной системе счисления?

Представление чисел в ЭВМ

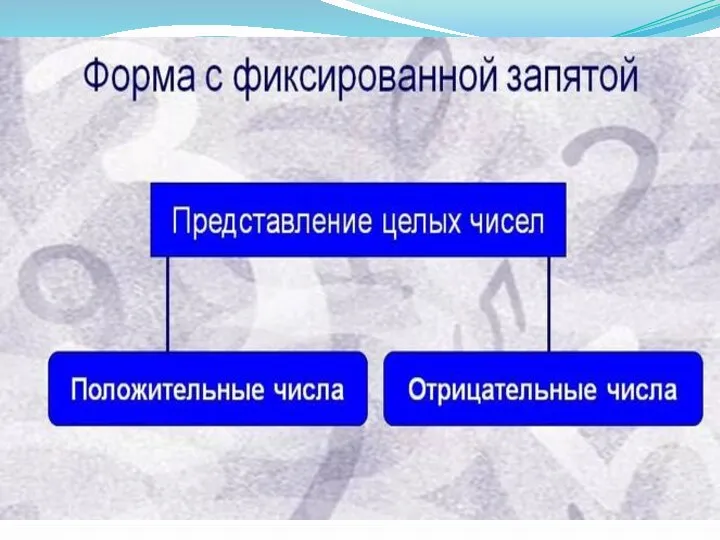
В ЭВМ применяются две формы представления чисел:
естественная форма или форма с фиксированной запятой (точкой)
и
нормальная форма или форма с плавающей запятой.
Представление чисел в ЭВМ

В форме представления с фиксированной запятой (точкой) числа изображаются в виде последовательности цифр с постоянным для всех чисел положением запятой, отделяющей целую часть от дробной.
В современных компьютерах естественная форма представления используется как вспомогательная и только для целых чисел.
Фиксированная запятая (точка)

Тип данных с плавающей точкой
(Floating point).
Естественная форма
Целочисленные типы данных отлично подходят для работы с целыми числами, но часто приходится работать и с дробными числами.
И тут на помощь приходит тип данных с плавающей точкой (floating point).
Еще его называют тип данных с плавающей запятой.
Например: 4320.0, -3.33 или 0.01226.
Почему точка «плавающая»?
Дело в том, что точка или запятая может двигаться («плавать») между цифрами, разделяя таким образом целую и дробную части в значении.

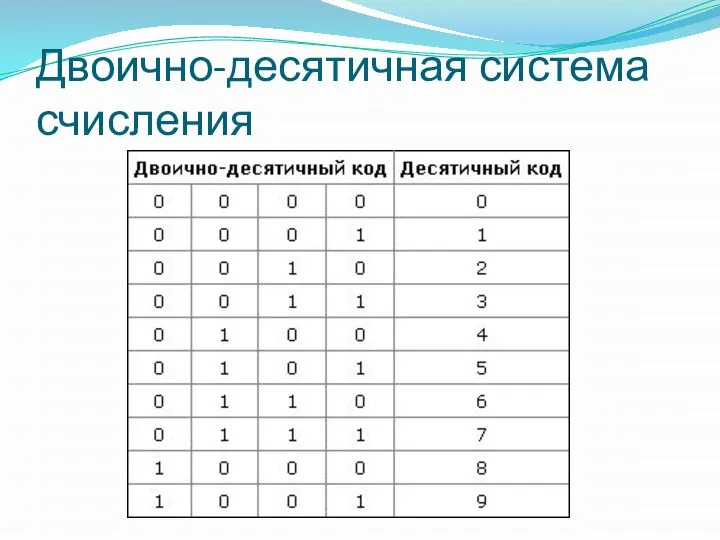
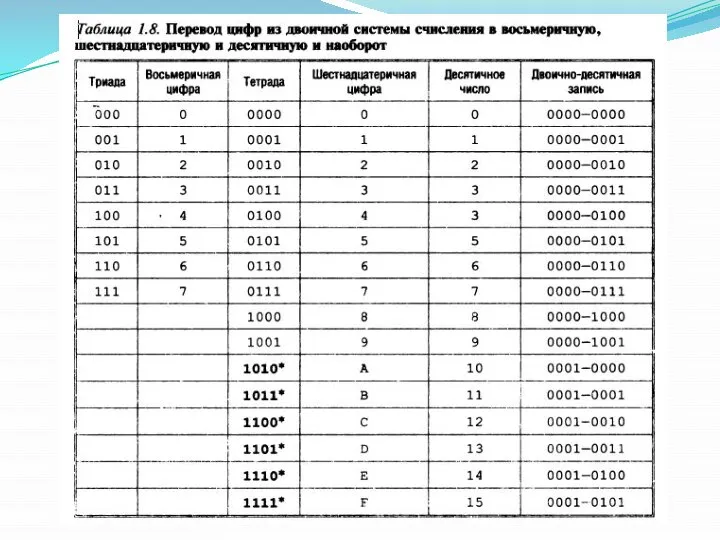
Двоично-десятичная система счисления получила большое распространение в современных компьютерах ввиду легкости перевода в десятичную систему и обратно.
Используется там, где важно удобство работы пользователя. В двоично-десятичной системе счисления основанием системы счисления является число 10, но каждая десятичная цифра (0, 1, ..., 9) кодируется четырьмя двоичными цифрами.
Двоично-десятичная система не экономична с точки зрения реализации технического построения машины (примерно на 20 % увеличивается требуемое оборудование), но более удобна при подготовке задач и при программировании.

Двоично-десятичная система счисления

Контрольные вопросы
Какие формы представления чисел используются в ЭВМ?
Какие числа хранятся в каждой форме?
Какие числа обрабатываются быстрее?
Для чего применяется двоично-десятичный код?
Что такое дополнительный и обратный код? Для чего он используется?

Прямой, обратный и дополнительный код
Входные и выходные данные представляются в форме, удобной для человека т.е. в 10-ой системе.
Для компьютера удобнее двоичная система.
Это объясняется тем, что технически гораздо проще реализовать устройства (например, запоминающий элемент) с двумя, а не с десятью устойчивыми состояниями (есть электрический ток — нет тока, намагничен — не намагничен и т.п.).

Любые данные (числа, символы, графические и звуковые образы) в компьютере представляются в виде последовательностей из нулей и единиц.
Обработку данных внутри компьютера можно воспринимать как преобразование слов из нулей и единиц по правилам, зафиксированным в микросхемах процессора.

Целые числа
Для представления чисел в ЭВМ обычно используют битовые наборы — последовательности нулей и единиц фиксированной длины.
Организовать обработку наборов фиксированной длины технически легче, чем наборов переменной длины.

Числа со знаком
Для представления знаковых целых чисел используются три способа:
1)прямой код;
2)обратный код;
3)дополнительный код.
Использование обратного и дополнительного кодов упрощается определение знака результата операции, вычитание есть сложение кодов, облегчено определение переполнения разрядной сетки

Положительные целые числа
Положительные числа в прямом, обратном и дополнительном кодах изображаются одинаково — цифровая часть содержит двоичную запись числа, в знаковом разряде содержится 0 (ноль)
k - Количество разрядов

Обратный код отрицательных чисел
Получается инвертированием всех цифр двоичного кода абсолютной величины числа, включая разряд знака: нули заменяются единицами, а единицы — нулями.
Пример (Количество разрядов - k = 8):

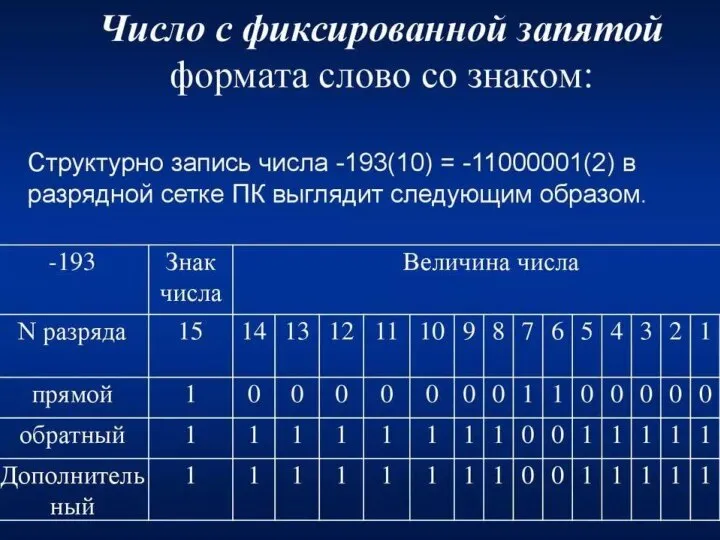
Дополнительный код отрицательных чисел
Дополнительный код — наиболее распространённый способ представления отрицательных целых чисел в компьютерах.
Позволяет заменить операцию вычитания на операцию сложения и сделать операции сложения и вычитания одинаковыми для знаковых и беззнаковых чисел, чем упрощает архитектуру ЭВМ.

Дополнительный код отрицательного числа получается инвертированием модуля двоичного числа и прибавлением к инверсии единицы, либо вычитанием числа из нуля.

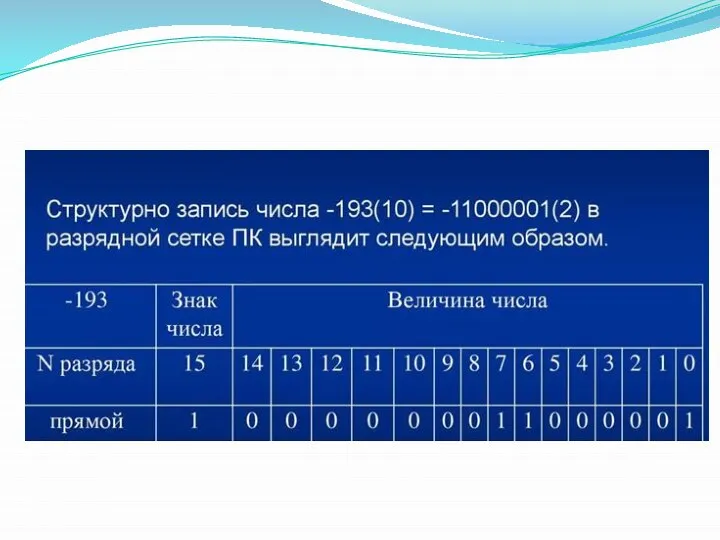
Пример
Двоичное 8-ми разрядное число с отрицательным знаком: x= - 01011101
Получаем прямой код: минус - знак числа записывается в виде 1, коды числа записываются без изменения:
X пр. = 1.01011101.
Для преобразования прямого кода двоичного отрицательного числа в обратный код знаковый разряд оставить без изменения, а в остальных разрядах нули заменить на единицы, а единицы на нули:
Xобр. = 1.10100010 .
Для получения дополнительного кода необходимо к младшему разряду числа в обратном коде добавить единицу:
Хдоп. = 1.10100011.
Для положительных двоичных чисел (в знаковом разряде записывается 0): X пр. = Xобр. = Хдоп.

Представление вещественных чисел
Вещественными числами называются числа, имеющие дробную часть.
Для хранения дробных чисел используется формат чисел с плавающей запятой

Тип данных с плавающей точкой. Floating point.
Формат для хранения вещественных чисел называют тип данных с плавающей запятой (floating point).
Например: 4320.0, -3.33 или 0.01226.
Почему запятая «плавающая»?
Дело в том, что точка или запятая может двигаться («плавать») между цифрами, разделяя таким образом целую и дробную части в значении.

Использование представления чисел с плавающей точкой существенно усложняет схему арифметико-логического устройства.
Для работы с числами с плавающей запятой выделена специальная часть процессора – математический сопроцессор

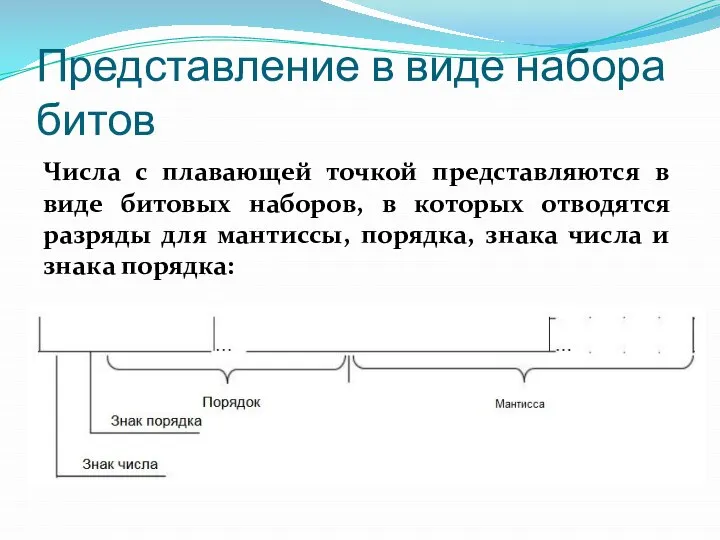
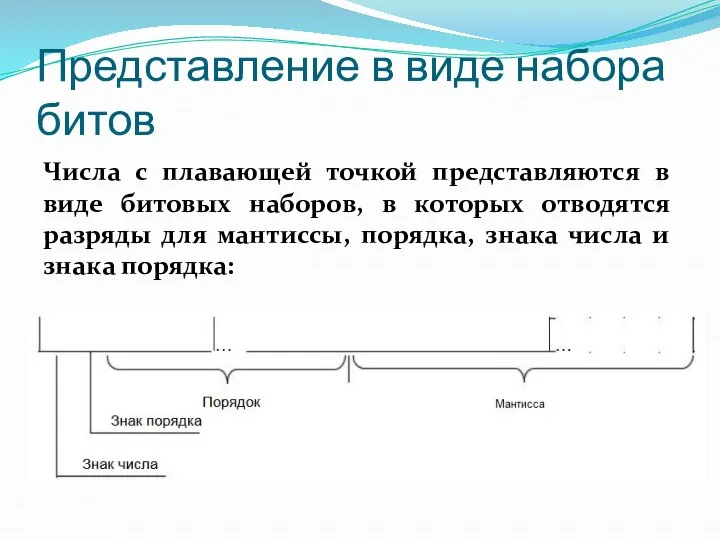
Представление в виде набора битов
Числа с плавающей точкой представляются в виде битовых наборов, в которых отводятся разряды для мантиссы, порядка, знака числа и знака порядка:

Чем больше разрядов отводится под запись мантиссы, тем выше точность представления числа.
Чем больше разрядов занимает порядок, тем шире диапазон от наименьшего отличного от нуля числа до наибольшего числа, представимого в машине при заданном формате.

Пример

Пример (отрицательное число)

Представление вещественных чисел
Вещественными числами называются числа, имеющие дробную часть.
Для хранения дробных чисел используется формат чисел с плавающей запятой

Тип данных с плавающей точкой. Floating point.
Формат для хранения вещественных чисел называют тип данных с плавающей запятой (floating point).
Например: 4320.0, -3.33 или 0.01226.
Почему запятая «плавающая»?
Дело в том, что точка или запятая может двигаться («плавать») между цифрами, разделяя таким образом целую и дробную части в значении.

Использование представления чисел с плавающей точкой существенно усложняет схему арифметико-логического устройства.
Для работы с числами с плавающей запятой выделена специальная часть процессора – математический сопроцессор

Представление в виде набора битов
Числа с плавающей точкой представляются в виде битовых наборов, в которых отводятся разряды для мантиссы, порядка, знака числа и знака порядка:

Чем больше разрядов отводится под запись мантиссы, тем выше точность представления числа.
Чем больше разрядов занимает порядок, тем шире диапазон от наименьшего отличного от нуля числа до наибольшего числа, представимого в машине при заданном формате.

Пример