Содержание
- 2. Логическое высказывание – это повествовательное предложение, относительно которого можно однозначно сказать, истинно оно (0) или ложно
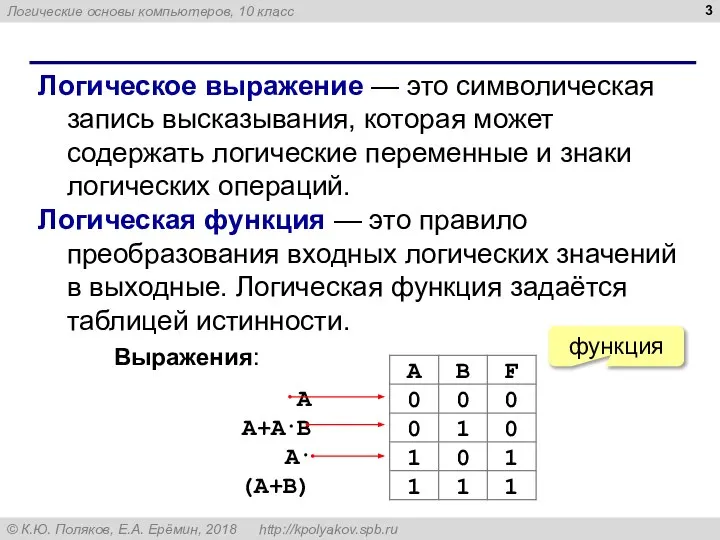
- 3. Логическое выражение — это символическая запись высказывания, которая может содержать логические переменные и знаки логических операций.
- 4. Операция НЕ (инверсия) Если высказывание A истинно, то «не А» ложно, и наоборот. 1 0 0
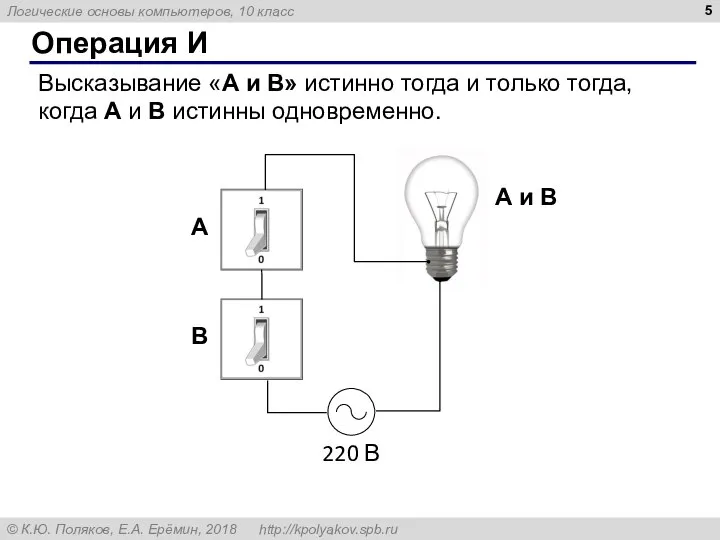
- 5. Операция И Высказывание «A и B» истинно тогда и только тогда, когда А и B истинны
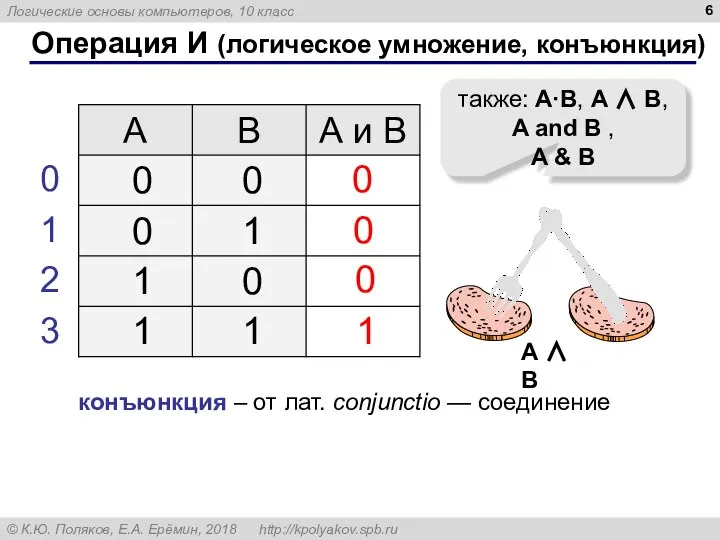
- 6. Операция И (логическое умножение, конъюнкция) 1 0 также: A·B, A ∧ B, A and B ,
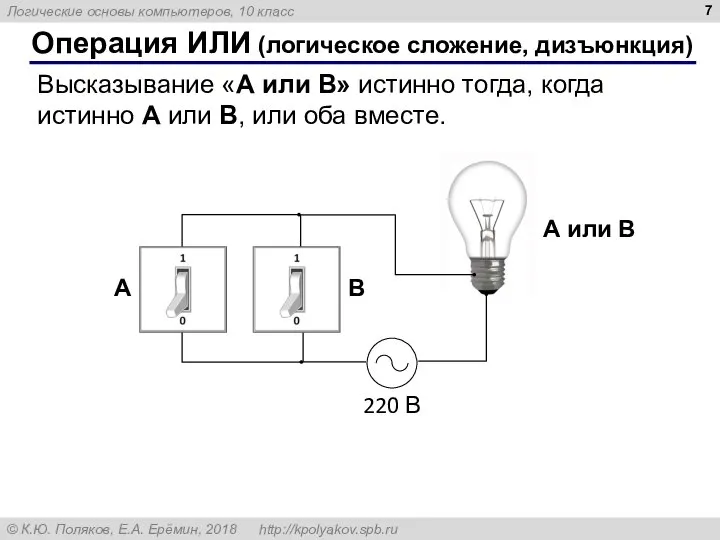
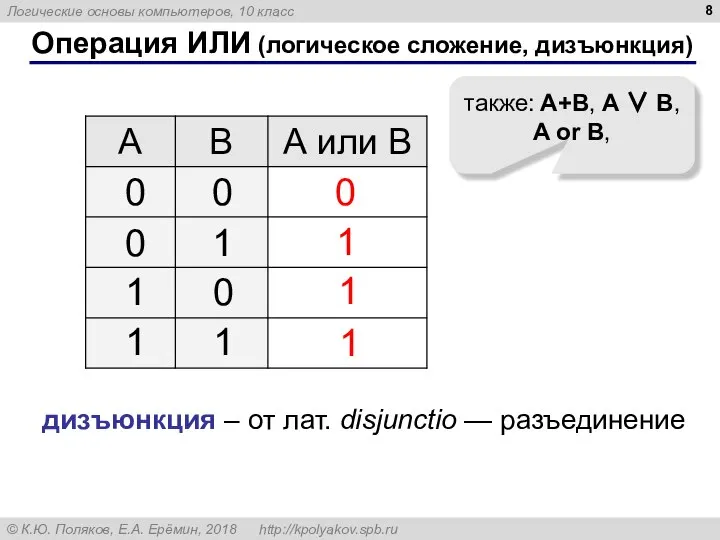
- 7. Операция ИЛИ (логическое сложение, дизъюнкция) Высказывание «A или B» истинно тогда, когда истинно А или B,
- 8. Операция ИЛИ (логическое сложение, дизъюнкция) 1 0 также: A+B, A ∨ B, A or B, 1
- 9. Импликация («если …, то …») Высказывание «A → B» истинно, если не исключено, что из А
- 10. Импликация («если …, то …») «Если Вася идет гулять, то Маша сидит дома». A – «Вася
- 11. Эквиваленция («тогда и только тогда, …») Высказывание «A ↔ B» истинно тогда и только тогда, когда
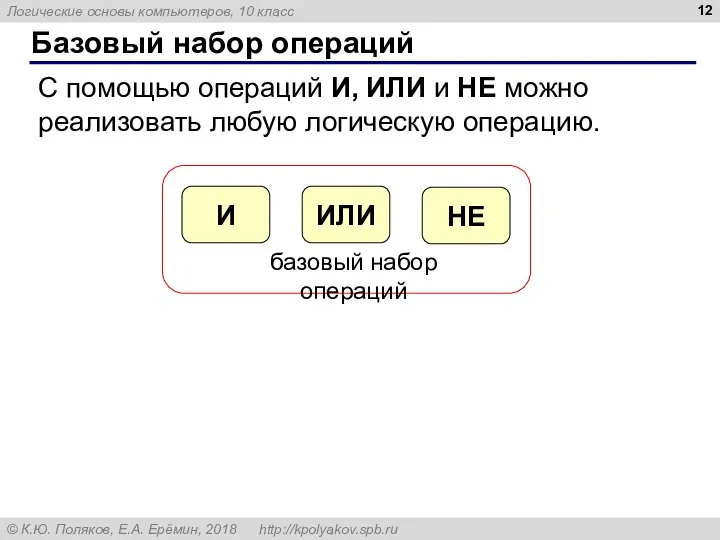
- 12. Базовый набор операций С помощью операций И, ИЛИ и НЕ можно реализовать любую логическую операцию.
- 13. Логические основы компьютеров Логические выражения
- 14. Вычисление логических выражений Порядок вычислений: скобки НЕ И ИЛИ импликация эквиваленция 1 4 2 5 3
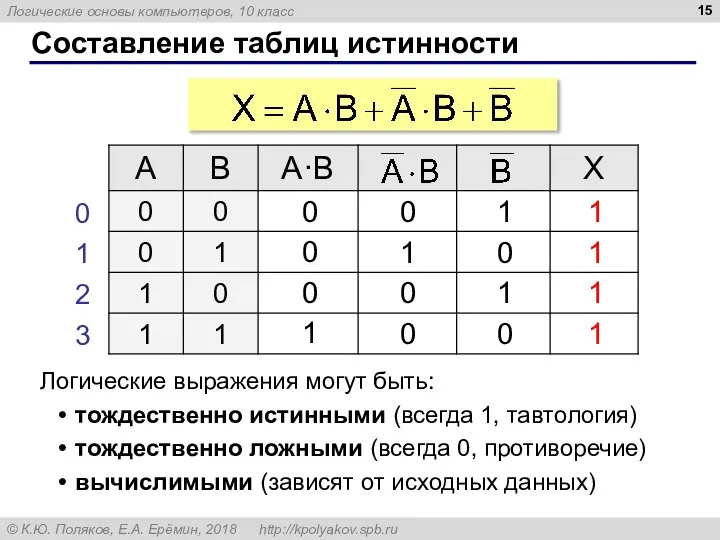
- 15. Составление таблиц истинности Логические выражения могут быть: тождественно истинными (всегда 1, тавтология) тождественно ложными (всегда 0,
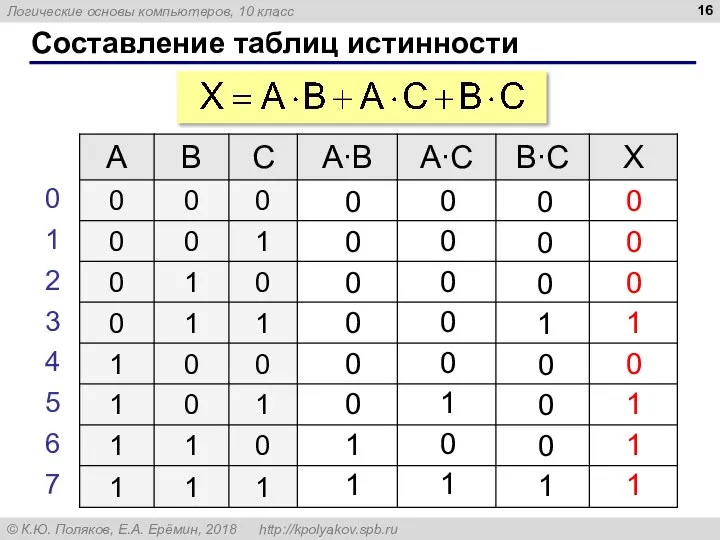
- 16. Составление таблиц истинности
- 17. Задачи Задача 1. При каких значениях логических переменных истинно выражение: Решение. Все сомножители равны 1: Задача
- 19. Скачать презентацию








 Основы web дизайна
Основы web дизайна Простейший графический редактор Paint. Сохранение и открытие рисунка
Простейший графический редактор Paint. Сохранение и открытие рисунка Игровые формы электронных интерактивных изданий
Игровые формы электронных интерактивных изданий Язык Паскаль. Матрицы
Язык Паскаль. Матрицы Формализация понятия Алгоритм
Формализация понятия Алгоритм Принципы создания личного бренда в социальных медиа
Принципы создания личного бренда в социальных медиа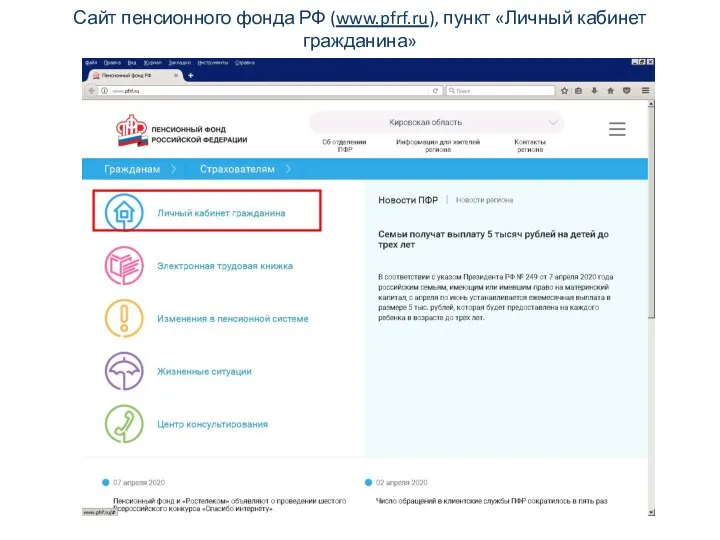 Заполнение интерактивной формы заявления. Сайт пенсионного фонда РФ
Заполнение интерактивной формы заявления. Сайт пенсионного фонда РФ Язык программирования Pascal
Язык программирования Pascal Периферийные устройства персонального компьютера. Программное обеспечение внешних устройств
Периферийные устройства персонального компьютера. Программное обеспечение внешних устройств Структура действия и структуры данных
Структура действия и структуры данных Все, все про Майнкрафт
Все, все про Майнкрафт Безопасный регион
Безопасный регион Выпускная квалификационная работа: применение XML технологий на MS SQL для сопровождения корпоративных приложений
Выпускная квалификационная работа: применение XML технологий на MS SQL для сопровождения корпоративных приложений Закупка трафика в плюс
Закупка трафика в плюс Презентація на тему : « ОРНАМЕНТИ ТА ВИДИ ОРНАМЕНТІВ. СИМВОЛИ В УКРАЇНСЬКІЙ НАРОДНІЙ ВИШИВЦІ » Роботу виконала Андріянова Аліна
Презентація на тему : « ОРНАМЕНТИ ТА ВИДИ ОРНАМЕНТІВ. СИМВОЛИ В УКРАЇНСЬКІЙ НАРОДНІЙ ВИШИВЦІ » Роботу виконала Андріянова Аліна Понятие алгоритма. Свойства алгоритма. Основные сведения об алгоритмах
Понятие алгоритма. Свойства алгоритма. Основные сведения об алгоритмах Функции, операторы, массивы
Функции, операторы, массивы SE-2222_DatabaseSecurity
SE-2222_DatabaseSecurity Триггеры в презентации. Создание слайдов с триггерами
Триггеры в презентации. Создание слайдов с триггерами Методика SMART
Методика SMART Определение каналов сбыта
Определение каналов сбыта Программное обеспечение: понятие, виды
Программное обеспечение: понятие, виды Компьютерные технологии обучения
Компьютерные технологии обучения Лекция 2
Лекция 2 Разбор задач ЕГЭ. Анализ программ с циклами и подпрограммами. В14
Разбор задач ЕГЭ. Анализ программ с циклами и подпрограммами. В14 Теория автоматов в программировании. Лекция 1
Теория автоматов в программировании. Лекция 1 Формирование информационной грамотности через работу с текстом на уроках окружающего мира
Формирование информационной грамотности через работу с текстом на уроках окружающего мира Мультимедиа в Театральном музее
Мультимедиа в Театральном музее