Логические основы работы компьютера

План изучения
Основные логические понятия.
Математическая логика.
Операции над высказываниями (логические операции).
Формы представления логических операций: логические функции, таблицы истинности, логические схемы.
5. Алгоритмы перевода представления логических операций из одной формы в другую
6. Алгебра логики и ее законы

Логика – наука о правилах рассуждений.
Логической функцией (функцией алгебры логики) от набора логических переменных F(х1, ..., хn) называется функция, которая может принимать только два значения: истина или ложь (1 или 0). Любая логическая функция может быть задана с помощью таблицы истинности, в левой части которой записываются возможные наборы значений аргументов, а в правой - соответствующие им значения функции.

Понятие о суждении
Познавая объективный мир, человек раскрывает связи между предметами и их признаками.
Эти связи и отношения отражаются
в мышлении в форме СУЖДЕНИЙ.
СУЖДЕНИЕ – это мысль, в которой что-либо утверждается или отрицается о предмете.
Языковой формой выражения суждения является предложение (высказывание).

Понятие о суждении
Не всякое предложение является суждением.
Не являются суждениями советы, просьбы,
вопросительные и восклицательные предложения.
Например:Закрой окно! Который час?
Суждение выражается повествовательным предложением.
Например: Я люблю информатику.
На улице хорошая погода. Иванов – двоечник.
СУЖДЕНИЕ – это повествовательное предложение, относительно которого имеет смысл говорить истинно оно или ложно.

Математическая логика
Основатель – Джордж Буль (1815-1864).
Математическая логика двузначна (истина, ложь)
Математическая логика изучает только суждения.
Причем смысл высказывания не имеет значения, принимается во внимание
только значение истинности.

Математическая логика
Значение истинного высказывания = 1
Значение ложного высказывания = 0
Для простоты высказывания обозначаются
латинскими буквами А, В, С…
У кошек четыре ноги. А=1
У кошек нет хвоста. В=0
Высказывания бывают простые и сложные.
Простые высказывания называются
логическими переменными (А, В, С).
Сложные – логическими функциями (А∨D∧C).

Алгебра логики
Начальный раздел математической логики называют алгеброй логики, или булевой алгеброй.
Использование 0 и 1 в качестве значений переменных в алгебре логики и цифр в двоичной системе счисления, позволяет описать работу логических схем ПК с помощью математического аппарата булевой алгебры.

Операции над высказываниями
Конъюнкция (логическое умножение)
союз И
обозначение ∧, &
конъюнкция двух логических переменных истинна только тогда, когда истинны обе переменные.
ТАБЛИЦА ИСТИННОСТИ:
ЛОГИЧЕСКИЙ ЭЛЕМЕНТ:
&

Операции над высказываниями
Дизъюнкция (логическое сложение)
союз ИЛИ
обозначение ∨
дизъюнкция двух логических переменных истинна, если истинна хотя бы одна переменная.
ТАБЛИЦА ИСТИННОСТИ:
ЛОГИЧЕСКИЙ ЭЛЕМЕНТ:
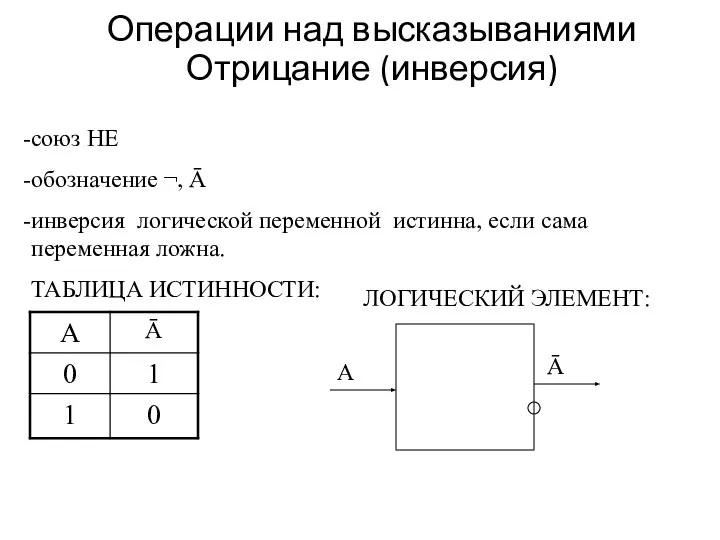
1

Операции над высказываниями
Отрицание (инверсия)
союз НЕ
обозначение ¬, Ā
инверсия логической переменной истинна, если сама переменная ложна.
ТАБЛИЦА ИСТИННОСТИ:
ЛОГИЧЕСКИЙ ЭЛЕМЕНТ:
А
Ā

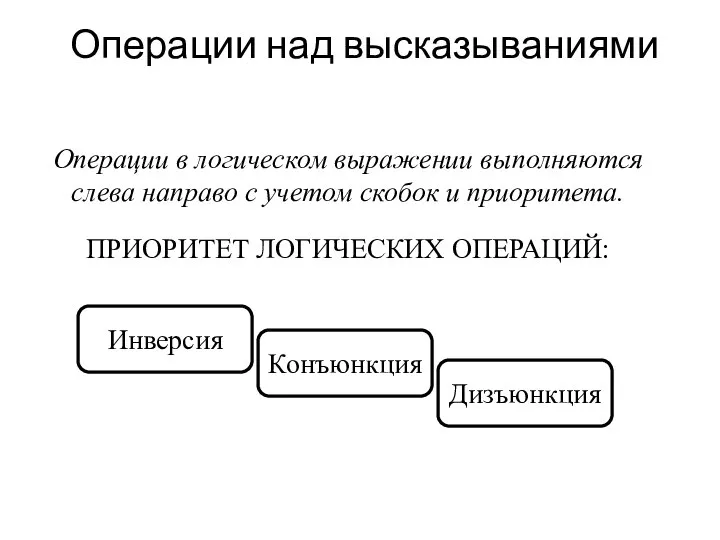
Операции над высказываниями
ПРИОРИТЕТ ЛОГИЧЕСКИХ ОПЕРАЦИЙ:
Операции в логическом выражении выполняются слева направо с учетом скобок и приоритета.
Инверсия
Конъюнкция
Дизъюнкция

Элементы алгебры логики
Высказывания бывают простые и сложные.
Простые высказывания называются
логическими переменными
и обозначаются латинскими буквами (А, В, С).
У всех кошек четыре ноги. А=1
У всех кошек нет хвоста. В=0
1 и 0 –константы алгебры логики
Сложные высказывания называются
логическими функциями.
F(A,C,D)= А∨D∧C

Логические функции
Логическая функция - это формализованная запись сложного высказывания на языке алгебры логики.

Таблицы истинности
Определить значение истинности сложного высказывания (функции от нескольких переменных) непросто.
Для этого составляют таблицу, в которой перечисляют все комбинации значений простых высказываний и, реализуя логическую связь, получают значения истинности сложного высказывания.

Таблицы истинности
Значения каждой логической функции
можно описать таблицей истинности.
ТАБЛИЦА ИСТИННОСТИ представляет собой таблицу, устанавливающую соответствие между возможными значениями наборов переменных
и значениями функции.
А ∨ В

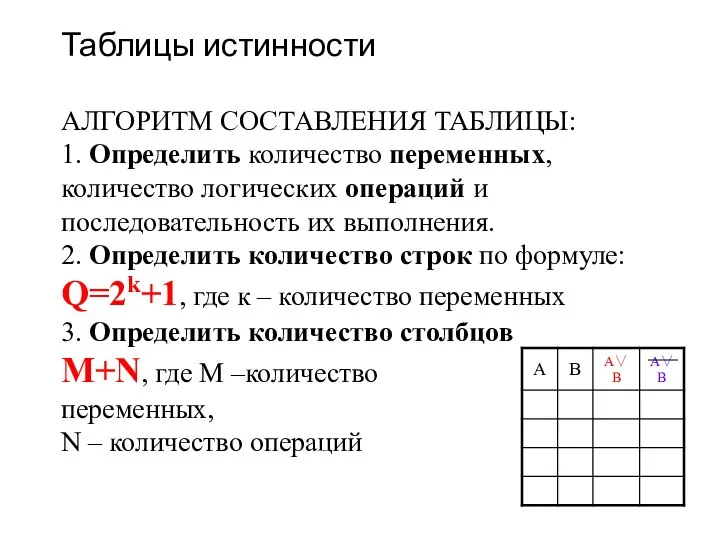
Таблицы истинности
АЛГОРИТМ СОСТАВЛЕНИЯ ТАБЛИЦЫ:
1. Определить количество переменных, количество логических операций и последовательность их выполнения.
2. Определить количество строк по формуле:
Q=2k+1, где к – количество переменных
3. Определить количество столбцов
М+N, где М –количество
переменных,
N – количество операций

Таблицы истинности
АЛГОРИТМ СОСТАВЛЕНИЯ ТАБЛИЦЫ:
4. Первыми расположить столбцы с переменными.
5. За ними по приоритету столбцы операций.
6. Заполнить столбцы переменных всеми возможными значениями.
7. Затем, последовательно выполняя операции, заполнять столбцы операций.

Таблицы истинности
АЛГОРИТМ СОСТАВЛЕНИЯ ТАБЛИЦЫ:
4. Первыми расположить столбцы с переменными.
5. За ними по приоритету столбцы операций.
6. Заполнить столбцы переменных всеми возможными значениями.
7. Затем, последовательно выполняя операции, заполнять столбцы операций.

Таблицы истинности
АЛГОРИТМ СОСТАВЛЕНИЯ ТАБЛИЦЫ:
4. Первыми расположить столбцы с переменными.
5. За ними по приоритету столбцы операций.
6. Заполнить столбцы переменных всеми возможными значениями.
7. Затем, последовательно выполняя операции, заполнять столбцы операций.

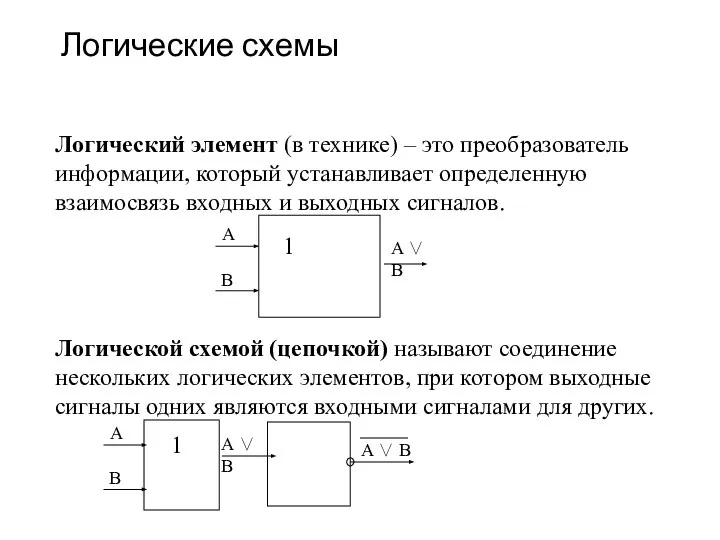
Логические схемы
Логический элемент (в технике) – это преобразователь информации, который устанавливает определенную взаимосвязь входных и выходных сигналов.
Логической схемой (цепочкой) называют соединение нескольких логических элементов, при котором выходные сигналы одних являются входными сигналами для других.
А
В
А ∨ В
1
А ∨ В

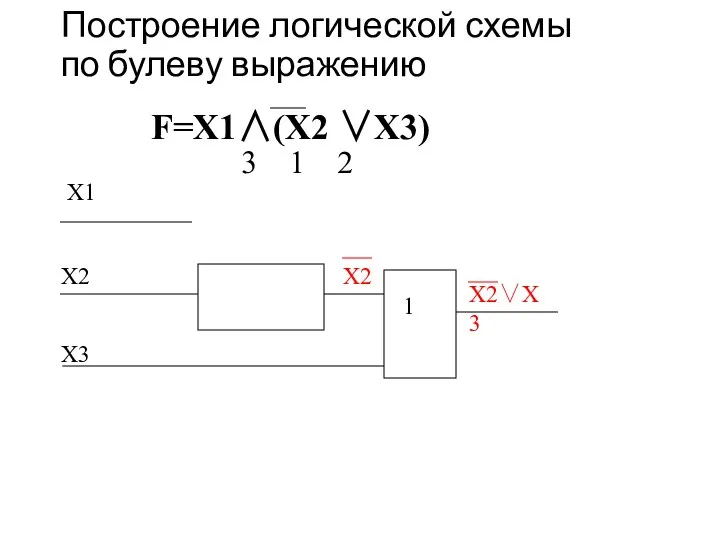
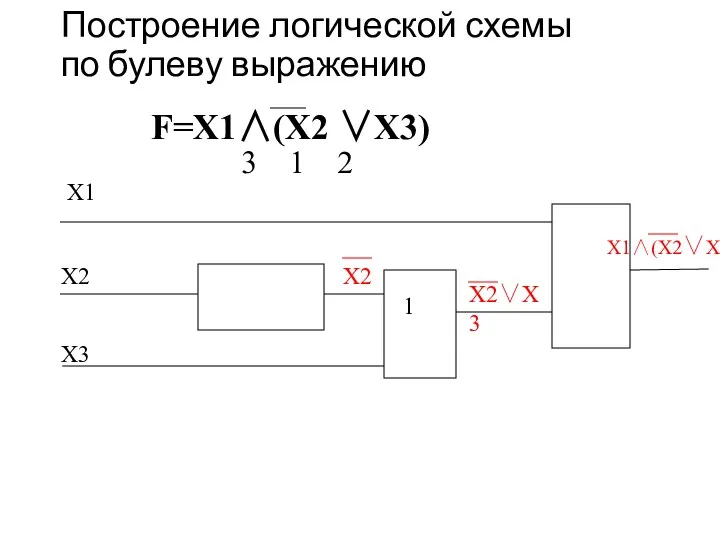
Построение логической схемы
по булеву выражению
F=X1∧(X2 ∨X3)
1. Определить приоритет операций.
F=X1∧(X2 ∨X3)
3 1 2
2. Определить количество и имена переменных.
3. Согласно приоритету дополнять в схему логические элементы, делая выходы предыдущих входами для последующих.

Построение логической схемы
по булеву выражению
F=X1∧(X2 ∨X3)
3 1 2
Х1
Х2
Х3

Построение логической схемы
по булеву выражению
F=X1∧(X2 ∨X3)
3 1 2
Х1
Х2
Х3
Х2

Построение логической схемы
по булеву выражению
F=X1∧(X2 ∨X3)
3 1 2
Х1
Х2
Х3
Х2
1
Х2∨Х3

Построение логической схемы
по булеву выражению
F=X1∧(X2 ∨X3)
3 1 2
Х1
Х2
Х3
Х2
1
Х2∨Х3
Х1∧(Х2∨Х3)

Упрощение логических формул
Упростить функцию, означает получить функцию равносильную данной, но содержащую меньшее число вхождений переменных или операций.
Например:
B∨A ∧Ā = B
(A ∧Ā) ∧B ∧C = B ∧C
(X∨Y) ∧X = X∧Y
Упрощение еще называют минимизацией функции, она необходима для того, чтобы функциональные схемы не были слишком громоздкими и не использовали лишних элементов.

Проектирование компьютеров не обходится без булевой алгебры начиная с 1938 года. Электрическая схема компьютера состоит из миллионов переключательных элементов.
Алгебра Буля позволяет проводить анализ этих схем, упростить их, тем самым исключить неоправданное усложнение электронных схем работы компьютеров.

Определите суждения
1. Завтра будет холодно.
2. 2*2=5
3. Какой ребенок не ждет Нового года?
4. Квадрат – это равносторонний прямоугольник.
5. Который час?
6. Идет дождь.
7. Идите сюда!
8. Завтра брат приедет к нам в гости.
9. 12 - число не простое.
10. 10+5=15
11. Луна – спутник Земли.
12. Принеси мне книгу.
13. Вы были в театре?
14. Мойте руки перед едой.
15. Все ученики нашей школы любят математику.

Определите истинность суждений
1. Логический элемент ИЛИ всегда имеет два и более входов.
2. Логические элементы И и ИЛИ всегда имеют два и более входов.
3. Логический элемент КОНЪЮНКЦИЯ обозначается знаком ∨.
4. Логический элемент ИНВЕРСИЯ всегда имеет один вход.
5. Все логические элементы всегда имеют ОДИН выход.
6. Логические элементы И и ИЛИ могут иметь ОДИН вход.
7. Логический элемент ИНВЕРСИЯ может иметь несколько входов.
8. ИНВЕРСИЯ означает ПЕРЕВОРАЧИВАНИЕ.
9. Логический элемент КОНЪЮНКЦИЯ обозначается знаком &.

Составьте таблицы истинности
F(A,B,C)=A∨(C∧B)
2. F(A,B,C)= B ∧C ∨ Ā
3. F(A,B,C)= (A∧B ∧C)
4. F(A,B,C)= (A∨B) ∧(A ∨C)
5. F(A,B,C,D)= (A∨B) ∧C ∧(B ∨D)
6. F(A,B,C,D)= (A∨B) ∨(C ∧(B ∨D)

Постройте логические схемы
F(A,B,C)=A∨(C∧B)
2. F(A,B,C)= B ∧C ∨ Ā
3. F(A,B,C)= (A∧B ∧C)
4. F(A,B,C)= (A∨B) ∧(A ∨C)
5. F(A,B,C,D)= (A∨B) ∧C ∧(B ∨D)
6. F(A,B,C,D)= (A∨B) ∨(C ∧(B ∨D)

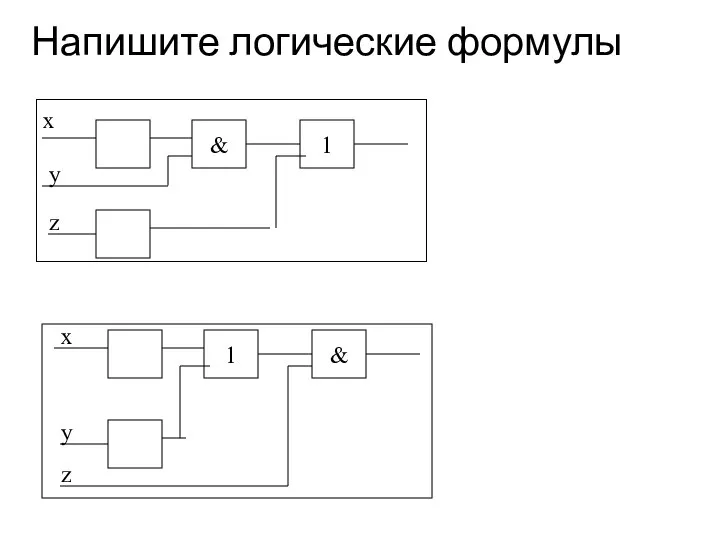
Напишите логические формулы
x
1
&
y
z
x

Запишите сложные высказывания
в виде логических формул
Можно пойти в магазин и на рынок или не выходить из дома.
2. Наташа или не была в школе или получила двойку.
3. Подозреваемый не врал и не изворачивался.
4. Оля не испугалась и продолжила путь.
5. Это могли сделать Саша и Вика или Коля и Таня.

Сформулируйте отрицания следующих высказываний
Саша занимается спортом.
2. Компьютер работает без сбоев.
3. На улице сухо.
4. Сегодня выходной день.
5. Антон сегодня не готов к урокам.
6. В школу поставили новые компьютеры.