Магистерская программа Моделирование в биотехническом приборостроении

Введение.
Методы планирования эксперимента особое значение приобрели в связи с крупными программами проведения и автоматизации научных исследований.
Применение методов планирования эксперимента может дать более или менее значительный экономический эффект, но отсутствие соответствующего плана может сделать экспериментальную программу полностью безрезультатной.
Это диктует необходимость подготовки специалистов различного уровня, владеющих уже известными методами планирования эксперимента и способных разрабатывать новые методы применительно к различным предметным областям.
Важный вопрос — это создание математической модели реального эксперимента. Переход к такой модели должен осуществляться в рамках соответствующей предметной области.
Для сельского хозяйства подобный переход требует понимания аграрных или животноводческих вопросов, в химии нужно иметь априорное понимание условий протекания соответствующих реакций: аналогичные проблемы возникают в физике, технике, биологии и др.

В каждой области существуют специфические ограничения, и только специалисты могут указать группы факторов, которыми можно пренебречь.
Специалист в конкретной предметной области редко владеет в полной мере математическим аппаратом. Обычно планирование реального эксперимента требует совместной работы группы специалистов.
Сравнительные эксперименты
Во многих областях экспериментирования следует отметить различие, между экспериментами, имеющими целью оценивание абсолютных констант, и сравнительными экспериментами.
Во многих экспериментах абсолютная характеристика может меняться неустойчиво, а относительная характеристика двух способов обработки (или процессов, или разновидностей и т. д.) оказывается довольно устойчивой. Можно утверждать, что в подобных обстоятельствах один способ обработки дает существенно лучшие результаты, чем другой, даже если мы не можем установить в точности, какие результаты дает каждый. В таких областях экспериментирования эксперименты, по-видимому, должны быть сравнительными.

В наших лекциях будут рассматриваться главным образом сравнительные эксперименты. Иначе говоря, они будут относиться скорее к таким предметам, как сравнение эффектов различных доз лекарства, чем к определению физических констант.
ПОНЯТИЕ ПЛАНА
Терминология
Эксперимент является важнейшей частью научного исследования.
Мы будем рассматривать лишь математические модели эксперимента. Это означает, что реальные физические, биологические и другие эксперименты будут фигурировать в дальнейшем изложении разве лишь в виде примеров.
Преимущество такого подхода состоит в общности. Каждая математическая модель оказывается приложимой во многих конкретных ситуациях.
Математические модели эксперимента тесно связаны с такими математическими дисциплинами, как теория вероятностей и математическая статистика.

Единицу материала, подвергаемую обработке, мы будем называть участком. В соответствии с исходным смыслом участок может быть площадкой земли, на которой созревает урожай, но он может быть и пациентом больницы, куском животной ткани, местом на теле животного, куда производится инъекция специального назначения, или одной из ряда однотипных машин.
Цель эксперимента состоит в сравнении эффектов различных способов обработки, каждый из которых применяется к одному или более участкам, с помощью количественной оценки результатов наблюдений, производимых на отдельных участках.
Любая количественная мера, полученная с участка, может быть названа урожаем.
Группа участков в структуре плана, имеющих некоторые присущие им общие черты, называется блоком.
Иногда испытываемые способы обработки объединены в несколько факторов (Факторный принцип).
Некоторые количественные или качественные состояния фактора называются уровнями.

Понятие плана
Под планом эксперимента понимают:
1) множество способов обработки, выбираемых для сравнения;
2) спецификацию обрабатываемых участков;
3) правила, по которым способы обработки следует размещать на участках;
4) спецификацию измерений или других данных, которые должны быть получены на каждом участке.
Обычно окончательное решение по пункту 1) принимает экспериментатор, хотя часто для оптимального выбора способов обработки имеется статистическая теория.
То, что можно было бы назвать классической теорией планирования экспериментов, заключено в пункте 3).
Статистик должен уметь делать полезные предложения по спецификации соответствующих участков.
Основными моментами, которые следует при этом иметь в виду, являются: а) пригодность, б) осуществимость, в) точность,
г) экономическая эффективность.

Рандомизация
Необходимым условием для получения несмещенных оценок разностей и их дисперсий является то, что принятое частное расположение выбрано случайным образом из множества всех возможных.
Этот случайный выбор, который достигается с помощью таблицы случайных чисел или других способов обеспечения безобидной лотереи, является сейчас, по общему признанию, существенной чертой планирования экспериментов.
План полностью определяется только с помощью множества всех допустимых расположений, из которых был выбран один действительно принятый план.
Изложение теории планирования мы будем проводить только для случая рандомизованных планов, если не оговорено противное.
Следовательно, спецификация плана должна включать формулировку одного или большего числа процессов требуемой рандомизации.

«Беспорядочное» расположение способов обработки или любое использование личного суждения при построении «случайных на вид» расположений не следует смешивать с точными процессами рандомизации, которые описаны в специальной литературе.
Во всех планах, описанных далее, рандомизация расположения способов обработки по участкам в пределах любого определенного блока или при сходных ограничениях является существенной для полной законности интерпретации.
Понятие случайного выбора наблюдений присуще всей теории вероятностей и всей теории статистического оценивания.
Подходящая рандомизация имеет то следствие, что в дисперсионном анализе при нулевой гипотезе о том, что способы обработки дают одинаковый эффект, средние квадраты для способов обработки и ошибок имеют равные математические ожидания.

Статистика
В математике слово «статистика» имеет два значения.
- Во-первых, так называется раздел математики, в котором по выборке (результатам экспериментов) определяется вид распределения, из которого была извлечена эта выборка, оцениваются параметры этого распределения, проверяются гипотезы о виде этого распределения.
- Второе значение слова «статистика» – это (измеримая) функция выборки. Поскольку элементы выборки суть случайные величины, то и статистика является случайной величиной.
Назначение статистик – оценка параметров распределения, из которого извлечена выборка.
В этом разделе собраны основные сведения из математической статистики, которые используются в планировании измерительных экспериментов.

Вероятность события. Случайным событиям можно приписать вероятность – число от нуля до единицы.
Понятие вероятности можно применять только к тем событиям, которые еще не произошли, или исход которых нам пока не известен.
Еще одним важным понятием является пространство событий – это полный набор всех возможных исходов.
Случайная величина — это переменная, значение которой до опыта (реализации) неизвестно.
Всякая случайная величина характеризуется:
множеством своих возможных значений
неограниченным числом повторения реализаций
вероятностью попадания в любую наперед заданную область во множестве значений.

Распределение случайной величины
Пусть X – это случайная величина, множеством возможных значений которой являются действительные числа. Рассмотрим вероятность события, что реализация X не больше заданного числа x. Если рассматривать эту вероятность в зависимости от величины x, то получится функция F(x), называемая (кумулятивной) функцией распределения случайной величины –
F(x) = Pr{X≤x}.
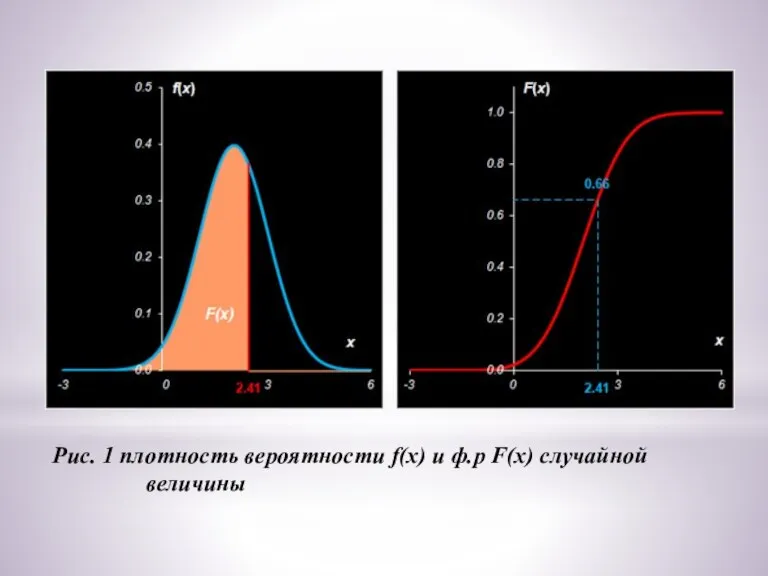
Функция распределения это неубывающая функция, которая стремится к 0 при малых x, и стремится к 1 при больших значениях аргумента.
Производная функция распределения F(x)называется плотностью вероятности f(x)

Рис. 1 плотность вероятности f(x) и ф.р F(x) случайной
величины

Математическое ожидание
Пусть X – это случайная величина с плотностью вероятности f(x). Математическим ожиданием X называется величина
Дисперсия и СKО
Пусть X – это случайная величина с плотностью вероятности f(x).
Дисперсией X называется величина
Если из дисперсии извлечь квадратный корень, то получится величина, называемая среднеквадратичным отклонением (СКО).

Основные распределения
Нормальное распределение
Нормальное (или гауссово) распределение – это, наверное, самое важное распределение в статистике. Плотность этого распределения имеет вид
Нормальное распределение зависит от двух параметров: m и σ2
и оно обычно обозначается N(m, σ2) т.е.
Математическое ожидание и дисперсия нормального распределения равны, соответственно (X)=m, V(X)=σ2.
Нормальное распределение называется стандартным, если
m=0, σ2=1.

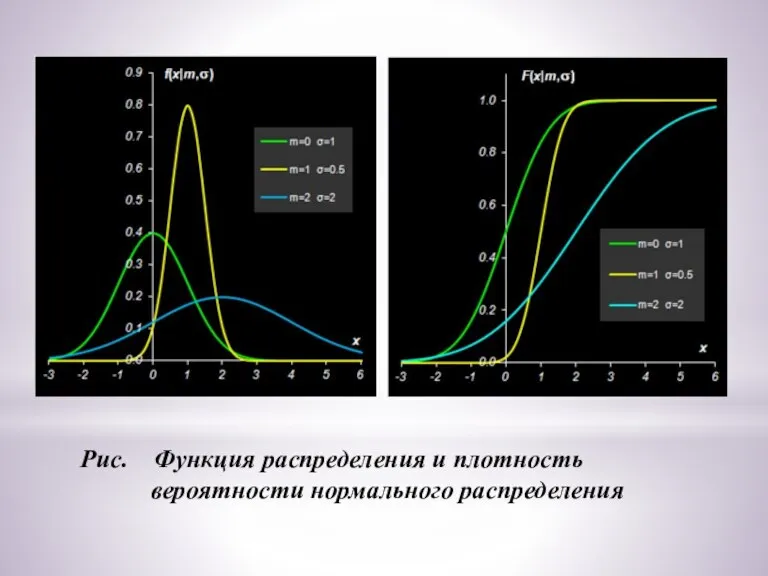
Рис. Функция распределения и плотность
вероятности нормального распределения

Распределение хи-квадрат
Рассмотрим N независимых стандартных нормальных случайных величин X1,…, Xn,…, XN
с нулевым мат. ожиданием и единичной дисперсией, т.е.
Xn ~ N(0, 1).
Величина
является случайной, распределение которой носит название хи-
квадрат. Это распределение зависит от одного параметра – N,
который называется числом степеней свободы.
Плотность вероятности распределения хи-квадрат имеет вид
Распределение хи-квадрат широко используется в статистике,
например, при проверке гипотез.

Рис. Функция распределения и квантиль распределения
хи-квадрат. Квантили распределения χ2(N)
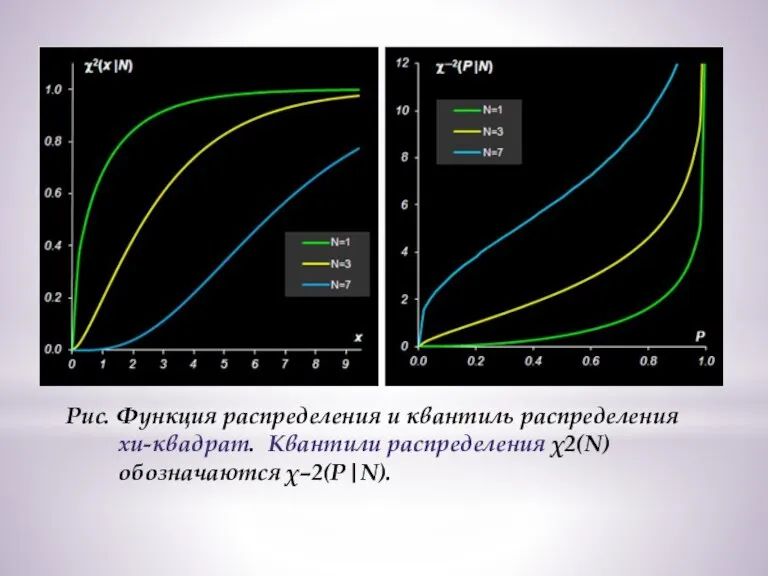
обозначаются χ–2(P|N).

Распределение Стьюдента
Рассмотрим две случайные величины: X – распределенную стандартно-нормально X ~ N(0, 1), и Y – распределенную по хи-квадрат с N степенями свободы Y ~ χ2(N).
Случайная величина
подчиняется распределению, которое носит имя Стьюдента.
Это распределение зависит от одного параметра N, который также называется числом степеней свободы.
Распределение Стьюдента применяется в проверке гипотез и для построения доверительных интервалов.

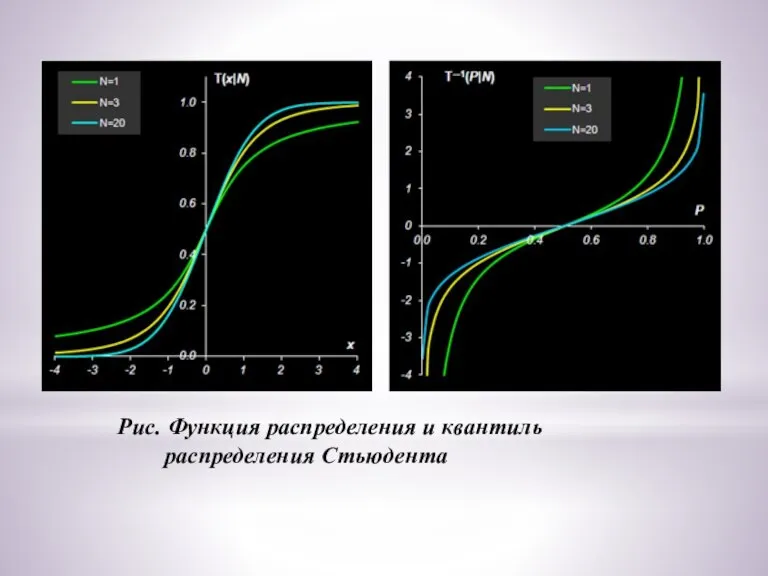
Рис. Функция распределения и квантиль
распределения Стьюдента

Распределение Фишера
Пусть имеются две независимые случайные величины X1 и X2 , каждая из которых подчиняется распределению хи-квадрат
с N1 и N2 степенями свободы, т.е.
X1 ~ χ2(N1) и X2 ~ χ2(N2).
Случайная величина
подчиняется распределению, которое носит имя Фишера.
Это распределение зависит от двух параметров N1 и N2, которые также называются числами степеней свободы.
Математическое ожидание и дисперсия распределения
F(N1, N2) равны , соответственно,
F(N1, N2))= N2/(N2 –2), N2>2

Рис. Функция распределения и квантиль распределения Фишера

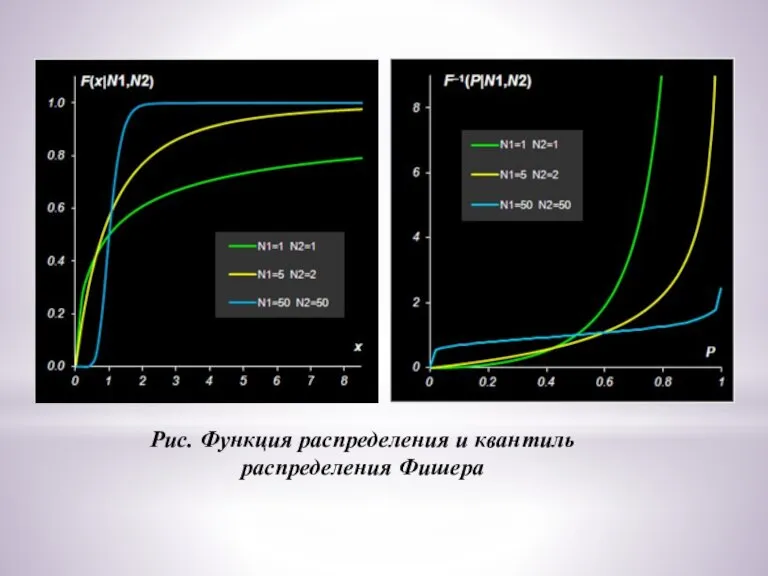
Генерация случайных чисел
Иногда бывает полезно создать искусственную выборку случайных чисел, подчиняющихся заданному распределению.
Это можно сделать, используя следующее простое утверждение.
Пусть F(x) и F–1(P) суть некоторая функция распределения и ее
квантиль, соответственно.
Если случайная величина X распределена равномерно на отрезке [0, 1], т.е
X ~ U(0,1),
тогда случайная величина
Y = F–1(X)
имеет функция распределения F.
Таким образом, если получить набор случайных величин, распределенных равномерно, то эти случайные величины можно превратить в новые, имеющие другое, заданное распределение.

Полностью рандомизованный план
Простейшим из всех планов, не представляющим самостоятельного математического интереса, но важным как в качестве основы для построения других планов, так и для практического применения, в ряде случаев является полностью рандомизованный план.
Суть этого плана состоит в том, что сначала выбирается число участков, к которым следует применить каждый из способов обработки, а затем производится рандомизация без каких-либо ограничений.
Если имеется N участков и t подлежащих сравнению способов обработки, то выбираются числа r1, r2, ..., rt подчиненные лишь условию
Тогда правило размещения состоит в следующем: выбираются случайным образом rt участков для первого способа обработки, из оставшихся участков выбираются на­угад r2 для второго способа и т. д., и последние rt уча­стков выделяются для способа обработки t.

Дисперсионный анализ в этом случае не представляет никаких трудностей и вытекает непосредственно из разбиения суммы квадратов. Вычисления сведены в табл.
*) Здесь Yp означает сумму rр урожаев с участков, подвергнутых обработке р;

Модели. Когда речь идет о критериях значимости и оценивании компонент дисперсии, модели важное значение приобретают модели .
Две основные модели можно проиллюстрировать, обратившись к полностью рандомизованному плану.
Урожай, в этом случае, на каком-либо участке может быть выражен равенством (*)
где η — общий средний урожай, который был бы получен, если бы каждый способ обработки можно было испытать по очереди на всех участках при одинаковых условиях,
a — средний урожай, который был бы получен,
если бы обработка р была применена к каждому участку.
Символ yip используется для обозначения того, что в принятой
конкретной рандомизации участок j (j = 1, 2, . . . , N) является
одним из rp (р = 1, 2, ..., t) участков, подвергнутых обработке р.
Остаток εj пред­ставляет собой величину, на которую истинный
урожай участка j отличается от среднего урожая для этого
спо­соба обработки.

В модели нормальных ошибок εj считается нормально распределенной величиной со средним нуль и дисперсией ϭ2, причем предполагается, что дисперсия одинакова для всех j, а распределения εj при различных j независимы.
Для более сложных планов обе эти модели уточняются включением дополнительных па­раметров в правую часть равенства (*), что дает воз­можность учесть эффекты наложенных ограничений.
Модель нормальных ошибок проще в том смысле, что если она применима, то отношения средних квадратов в дисперсионном анализе (для полностью рандомизованных и других планов) следуют распреде­лению дисперсионного отношения, когда верны соответ­ствующие нулевые гипотезы.

Компоненты дисперсии. При применении дисперсионного анализа может появиться необходимость вычислить математи-ческие ожидания средних квадратов при использованной процедуре рандомизации.
Для полностью рандомизованного плана в модели нормальных ошибок они могут быть получены с помощью формул
Тогда легко показать, что средний квадрат «внутри способов обработки» в дисперсионном анализе имеет математическое ожидание ϭ2 и, таким образом, не зависит от τp. По этой причине для него обычно используют название «ошибки».
Математическое ожидание среднего квадрата «между способами обработки» равно