Криптографические методы защиты информации. Лекция 1

№ 1 Введение в криптографические методы
№ 2 Основы теоретико-информационной стойкости
№ 3 Симметричное шифрование
№ 4 Асимметричное шифрование
№ 5 Электронная цифровая подпись
№ 6 Современные средства криптозащиты
Содержание дисциплины

ВВЕДЕНИЕ В ПРЕДМЕТ
Информация – фундаментальное, многозначное понятие.
Будем понимать под этим термином сведения, являющиеся объектом сбора (накопления), хранения, обработки (преобразования), непосредственного использования и передачи.
Простейшая модель передачи информации
(рисуем)

Потребность гражданского общества в специалистах по защите информации.
Специалисты в области информационной безопасности необходимы и в государственных структурах, и в научных учреждениях, и в коммерческих фирмах.
ВВЕДЕНИЕ В ПРЕДМЕТ

ЗИ – совокупность мероприятий и действий, направленных на обеспечение конфиденциальности и целостности в процессе сбора, передачи, обработки и хранения.
Безопасность информации:
– конфиденциальность (секретность, смысловая и информационная скрытность),
– сигнальная скрытность (энергетическая и структурная),
– целостность (устойчивость к разрушающим, имитирующим и искажающим воздействиям и помехам).
ВВЕДЕНИЕ В ПРЕДМЕТ

Криптографическое преобразование данных является наиболее эффективным и универсальным, а при передаче по протяженным линиям связи – единственным реальным средством предотвращения несанкционированного доступа к ней.
Принципиально не обойтись без криптографии при защите данных, передаваемых по открытым электронным каналам связи, а также там, где необходимо подтверждать целостность электронной информации или доказывать ее авторство.
ВВЕДЕНИЕ В ПРЕДМЕТ

Смарт-карты,
электронная почта,
системы банковских платежей,
торговля через Интернет,
электронный документооборот,
системы электронного голосования и т.д.
ВВЕДЕНИЕ В ПРЕДМЕТ

Для тайной передачи информации есть три возможности:
Создать абсолютно надежный, недоступный для других канал связи между абонентами
Использовать общедоступный канал связи, но скрыть сам факт передачи информации
Использовать общедоступный канал связи, но передавать по нему нужную информацию в так преобразованном виде, чтобы восстановить ее мог только адресат
ВВЕДЕНИЕ В ПРЕДМЕТ

Криптография – наука о шифрах – долгое время была засекречена, так как применялась, в основном, для защиты государственных и военных секретов.
В настоящее время методы и средства криптографии используются для обеспечения информационной безопасности не только государства, но и частных лиц, и организаций.
Наиболее надежные методы защиты от таких угроз дает именно криптография.
ВВЕДЕНИЕ В ПРЕДМЕТ

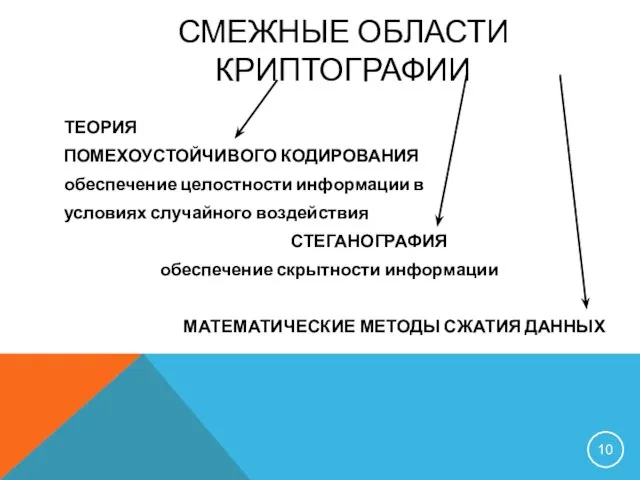
СМЕЖНЫЕ ОБЛАСТИ КРИПТОГРАФИИ
ТЕОРИЯ
ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ
обеспечение целостности информации в
условиях случайного воздействия СТЕГАНОГРАФИЯ
обеспечение скрытности информации
МАТЕМАТИЧЕСКИЕ МЕТОДЫ СЖАТИЯ ДАННЫХ

ЭТАПЫ РАЗВИТИЯ КРИПТОГРАФИИ
(ПО ТЕХНОЛОГИЧЕСКИМ ХАРАКТЕРИСТИКАМ МЕТОДОВ ШИФРОВАНИЯ)
Наивная криптография (до начала XVI в.)
Формальная криптография (конец XV в. – начало ХХ в.)
Научная криптография (30-60 гг. ХХ в.)
Компьютерная криптография (с 70 гг. ХХ в.)

ОСНОВНЫЕ ЧЕРТЫ НАИВНОЙ КРИПТОГРАФИИ
Использование любых способов запутывания противника относительно содержания шифруемых текстов.
Применение шифров перестановки или моноалфавитной подстановки (основной принцип — замена алфавита исходного текста другим алфавитом через замену букв другими буквами или символами).

ШИФРЫ НАИВНОЙ КРИПТОГРАФИИ
Атба́ш (ивр. אתב"ש‎) - простой шифр подстановки .
Правило шифрования: замена i-й буквы алфавита буквой с номером n на (i + 1)-ю букву, где n — число букв в алфавите.
ОТ:
abcdefghijklmnopqrstuvwxyz
ШТ:
ZYXWVUTSRQPONMLKJIHGFEDCBA

ШИФРЫ НАИВНОЙ КРИПТОГРАФИИ
Скитала (шифр древней Спарты)
Аполлоний Родосский (середина III века до н. э.)
Плутарх (около 45—125 н. э.)

ШИФРЫ НАИВНОЙ КРИПТОГРАФИИ
Квадрат Полибия
Изобретен во II веке до н. э. в Древней Греции

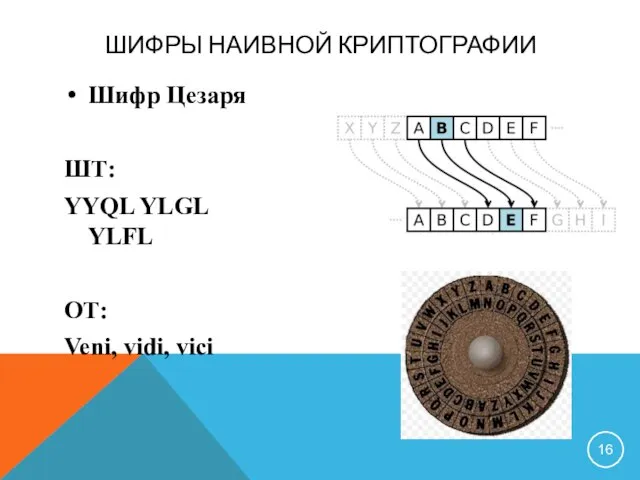
ШИФРЫ НАИВНОЙ КРИПТОГРАФИИ
Шифр Цезаря
ШТ:
YYQL YLGL YLFL
ОТ:
Veni, vidi, vici

ШИФРЫ НАИВНОЙ КРИПТОГРАФИИ
Тайнопись
Полная замена одного алфавита на другой

ОСНОВНЫЕ ЧЕРТЫ ФОРМАЛЬНОЙ КРИПТОГРАФИИ
Формализованные и относительно стойкие к ручному криптоанализу шифры.
Шифры многоалфавитной подстановки.

ТРУДЫ ПО КРИПТОГРАФИИ ЭПОХИ ВОЗРОЖДЕНИЯ
Роджер Бэкон (XIII в.) «Послание монаха Роджера Бэкона о тайных действиях искусства и природы и ничтожестве магии» (лат. «Epistola Fratris Rog. Baconis, de secretis operibus artis et naturae et nullitate magiae»)
7 методов скрытия текста

ТРУДЫ ПО КРИПТОГРАФИИ ЭПОХИ ВОЗРОЖДЕНИЯ
Леон Баттиста Альберти (1404-1472)
«Трактат о шифре» (1466) Идея мноноалфавитных шифров.

ТРУДЫ ПО КРИПТОГРАФИИ ЭПОХИ ВОЗРОЖДЕНИЯ
Иоганн Тритемий (1462-1516)
«Полиграфия» (1518)
Способ заполнения полибианского квадрата.
Шифрование пар букв (биграмм)
Шифр Виженера

ШИФРЫ ФОРМАЛЬНОЙ КРИПТОГРАФИИ
Решётка Кардано

ШИФРЫ ФОРМАЛЬНОЙ КРИПТОГРАФИИ
Шифр Плейфера
Чарльз Уитстон (1802-1875) Шифрование «двойным квадратом»

ШИФРЫ ФОРМАЛЬНОЙ КРИПТОГРАФИИ
Механические роторные машины
1790-е
Томас Джефферсон (1743-1826)
1817 г.
Чарльз Уитстон

ШИФРЫ ФОРМАЛЬНОЙ КРИПТОГРАФИИ

ПРАВИЛО КЕРКХОФФА
Огюст Керкгоффс (1835—1903)
«Военная криптография» (1883)
Секретность шифров должна быть основана на секретности ключа, но не алгоритма

ИСТОКИ НАУЧНОЙ КРИПТОГРАФИИ
Жан-Франсуа Шампольон, труд «Краткий очерк иероглифической системы древних египтян или исследования элементов этого письма», 1824 г.
Публикация метода Касиски (1863).
Огюст Керкгоффс, труд «Военная криптография», 1883.
Уильям Ф. Фридман, «Индекс совпадения и его применение в криптографии», 1918.
Введение терминов «криптология» и «криптография» (1920, Фридман).
Появление электромеханических машин (1920-е).
Лестер Хилл, публикация в журнале «The American Mathematical Monthly» статьи «Cryptography in an Algebraic Alphabet», 1929

ИСТОКИ НАУЧНОЙ КРИПТОГРАФИИ
К началу 30-х годов окончательно сформировались разделы математики, являющиеся научной основой криптологии - общая алгебра, теория чисел, теория вероятностей и математическая статистика.
К концу 1940-х годов построены первые программируемые счётные машины, заложены основы теории алгоритмов, кибернетики

ОСНОВНЫЕ ЧЕРТЫ НАУЧНОЙ КРИПТОГРАФИИ
Появление криптосистем со строгим математическим обоснованием криптостойкости
Появление теоретических принципов криптографической защиты информации

ПОДХОД К КРИПТОГРАФИИ КАК МАТЕМАТИЧЕСКОЙ НАУКЕ
Клод Шеннон
«Теория связи в секретных системах» (Communication Theory of Secrecy Systems) — секретный доклад, представленный автором в 1945 г., опубликован в «Bell System Technical Journal» в 1949 г.

Криптография как научная дисциплина молода:
строгое математическое обоснование криптостойкости появилось только в 30-60 годах XX века, а возможность большой скорости шифрования и увеличения криптостойкости в разы обеспечили вычислительные системы с 70-х годов XX века.
ВВЕДЕНИЕ В ПРЕДМЕТ

Клод Шеннон
Доклад "Математическая теория криптографии" (1945 г.)
Рассекречен и опубликован в 1948 г.
Переведен на русский язык в 1963 г.
Шеннон смог получить верхнюю оценку на длину шифртекста, которую необходимо учитывать для того, чтобы при криптоанализе достичь любого требуемого уровня достоверности его раскрытия.
ВВЕДЕНИЕ В ПРЕДМЕТ

Для профессионального понимания криптографических алгоритмов и умения оценивать их сильные и слабые стороны необходима серьезная математическая подготовка (на уровне математических факультетов университетов).
Это объясняется том, что современная криптография основана на глубоких результатах таких разделов математики, как
ВВЕДЕНИЕ В ПРЕДМЕТ

МАТЕМАТИЧЕСКИЕ ОСНОВЫ КРИПТОГРАФИИ
общая алгебра теория чисел
теория вероятностей
и математическая статистика
теория алгоритмов теория информации
теория вычислительной сложности
кибернетика

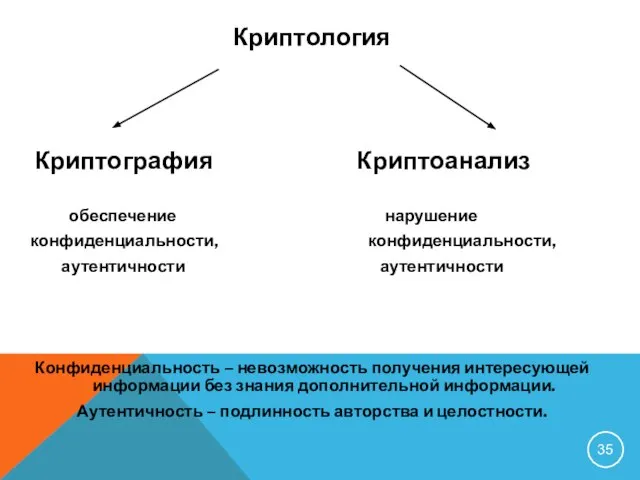
Криптология
Криптография Криптоанализ
обеспечение нарушение
конфиденциальности, конфиденциальности,
аутентичности аутентичности
Конфиденциальность – невозможность получения интересующей информации без знания дополнительной информации.
Аутентичность – подлинность авторства и целостности.

СТОЙКОСТЬ КРИПТОСИСТЕМЫ
Количество усилий, потраченных квалифицированными криптоаналитиками при неудачных попытках ее раскрытия
Теория информации:
Криптограф уповает на то, что криптоаналитик
не будет располагать достаточной информацией
для того, чтобы дешифровать криптограмму
Теория сложности вычислений:
Криптограф рассчитывает только на то,
что у криптоаналитика не хватит времени,
чтобы дешифровать криптограмму

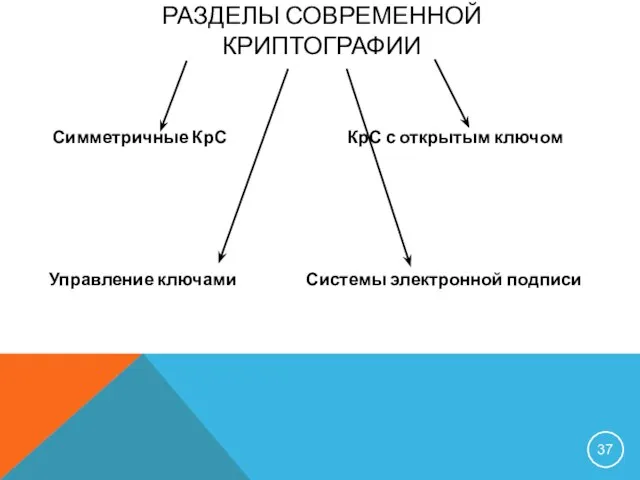
РАЗДЕЛЫ СОВРЕМЕННОЙ КРИПТОГРАФИИ
Симметричные КрС КрС с открытым ключом
Управление ключами Системы электронной подписи