Содержание
- 2. Методика решения заданий типа «Робот в лабиринте»
- 3. Задания этого типа сводятся к тому, чтобы определить те точки (назовем их «особые») в лабиринте, к
- 4. Задача: Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости: вверх вниз влево вправо
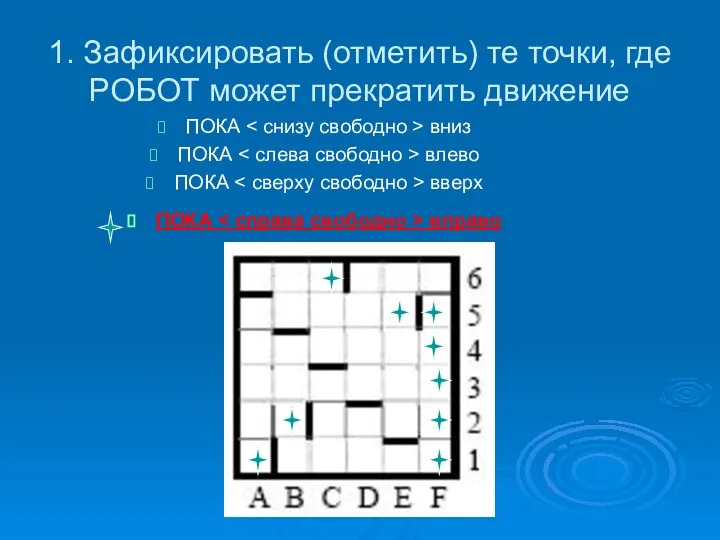
- 5. 1. Зафиксировать (отметить) те точки, где РОБОТ может прекратить движение ПОКА вниз ПОКА влево ПОКА вверх
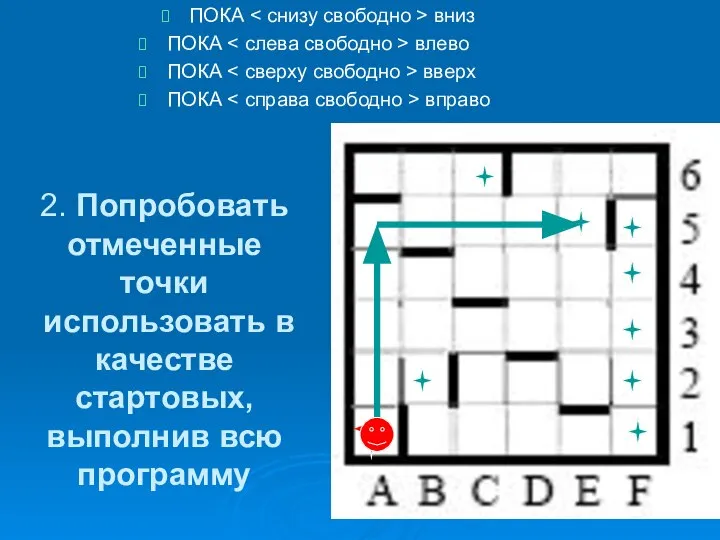
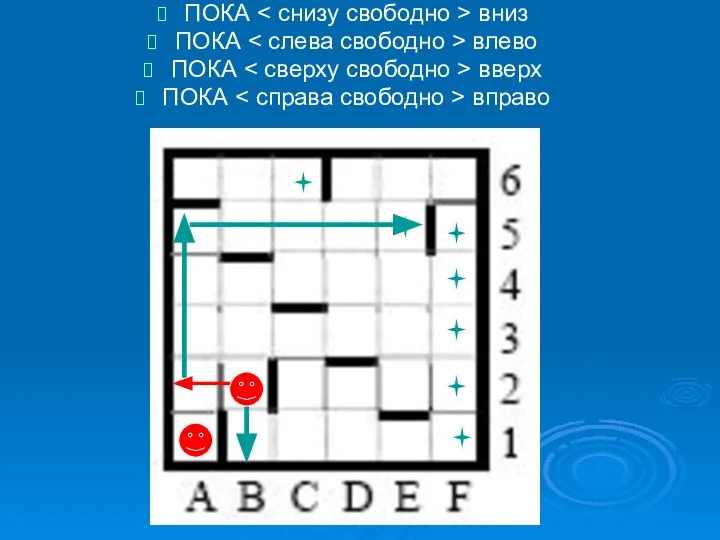
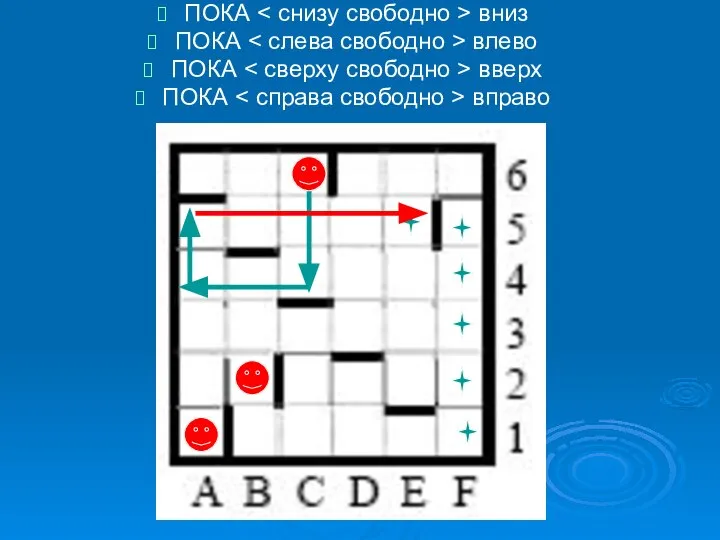
- 6. 2. Попробовать отмеченные точки использовать в качестве стартовых, выполнив всю программу ПОКА вниз ПОКА влево ПОКА
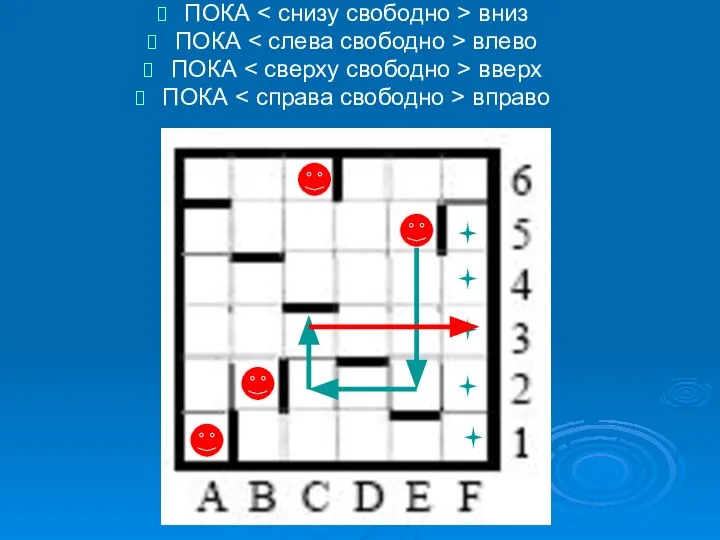
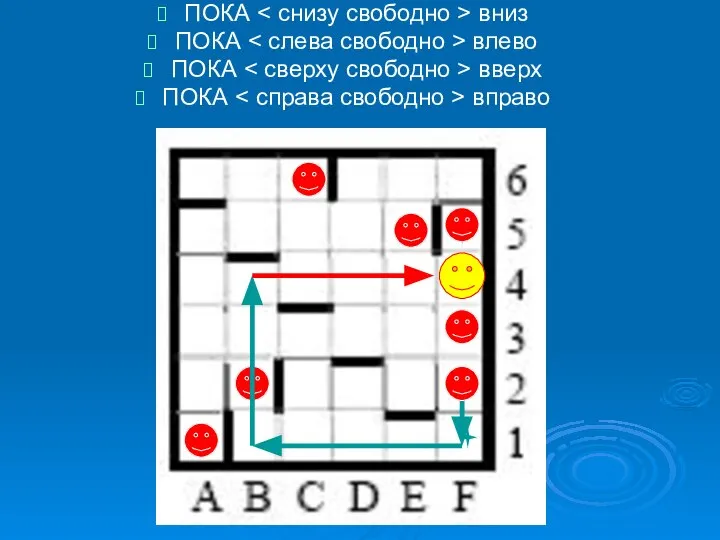
- 7. ПОКА вниз ПОКА влево ПОКА вверх ПОКА вправо
- 8. ПОКА вниз ПОКА влево ПОКА вверх ПОКА вправо
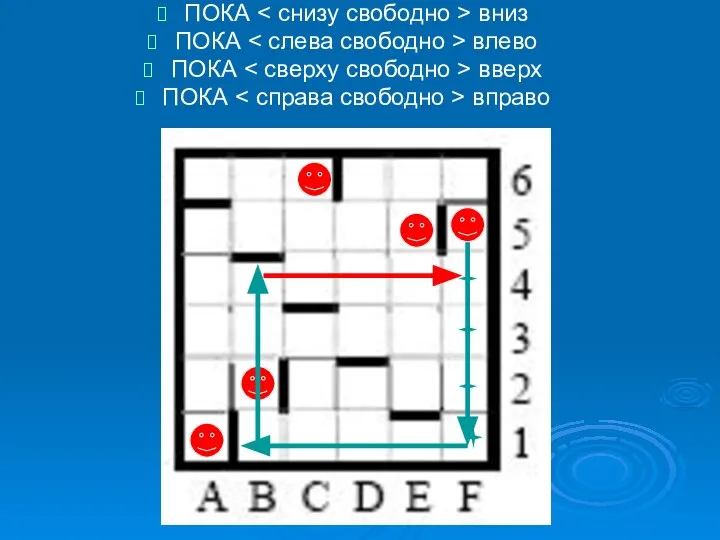
- 9. ПОКА вниз ПОКА влево ПОКА вверх ПОКА вправо
- 10. ПОКА вниз ПОКА влево ПОКА вверх ПОКА вправо
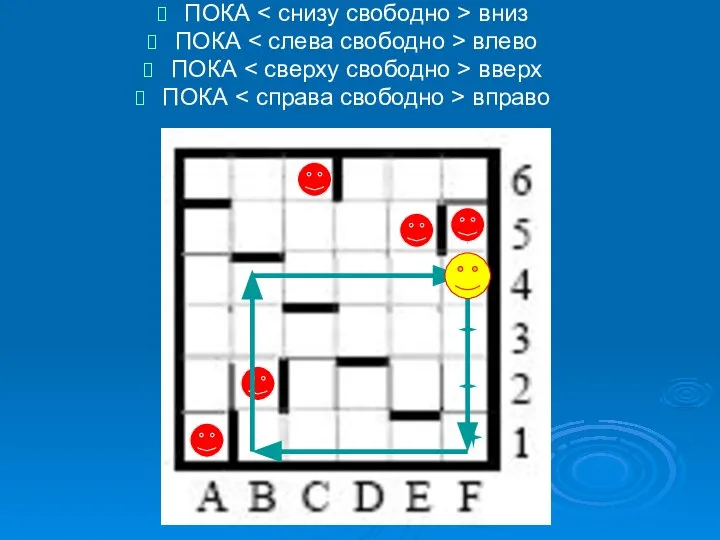
- 11. ПОКА вниз ПОКА влево ПОКА вверх ПОКА вправо
- 12. ПОКА вниз ПОКА влево ПОКА вверх ПОКА вправо
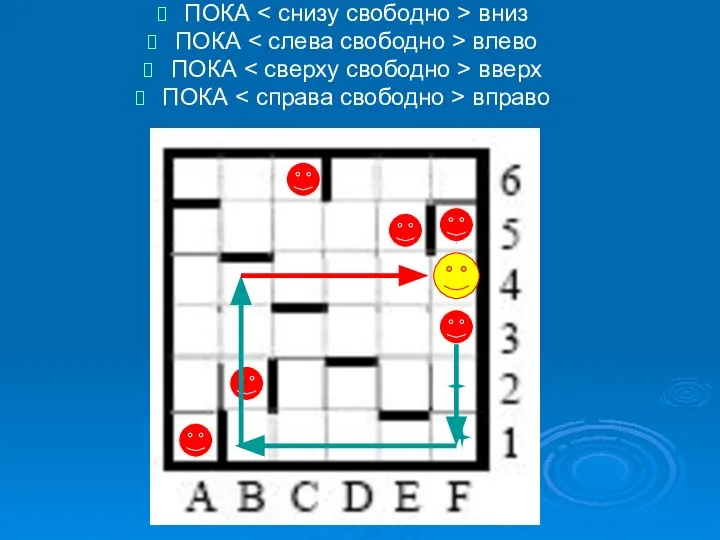
- 13. ПОКА вниз ПОКА влево ПОКА вверх ПОКА вправо
- 14. ПОКА вниз ПОКА влево ПОКА вверх ПОКА вправо
- 15. Ответ: Требованию «РОБОТ должен вернуться в исходную точку» удовлетворяет одна клетка. Ответ 1.
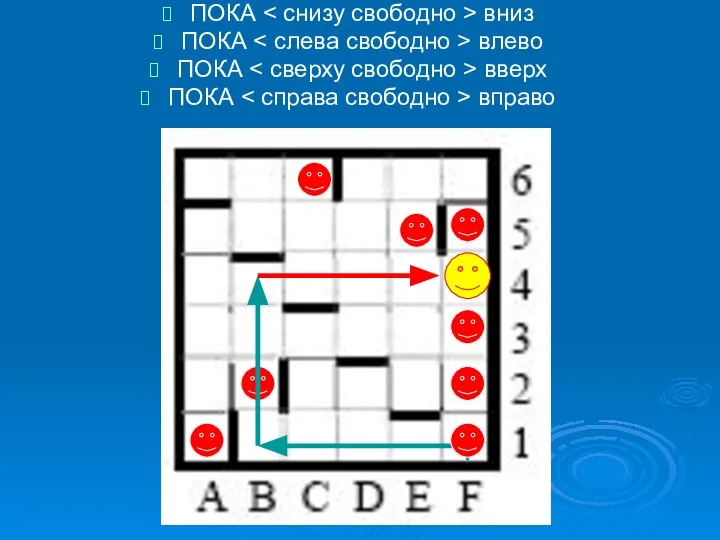
- 16. F Сколько клеток приведенного лабиринта соответствуют требованию, что, выполнив предложенную ниже программу, РОБОТ уцелеет (не врежется
- 17. Решение: особенность этой задач в том, что РОБОТ проверяет стенку в одном направлении, а движется в
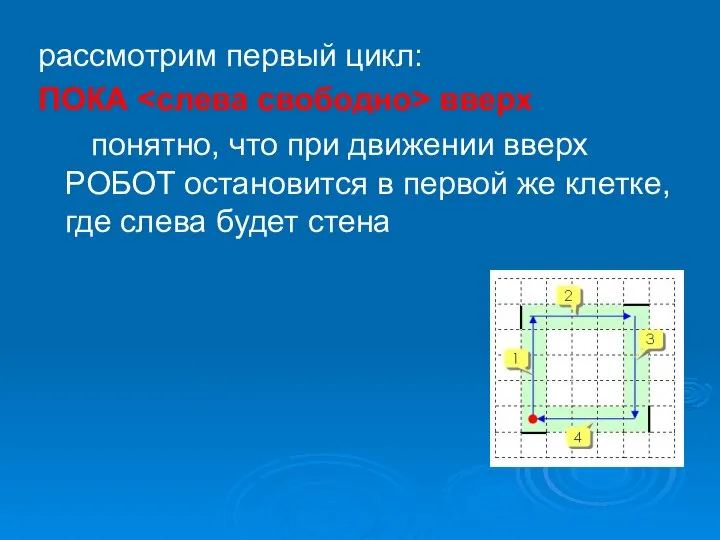
- 18. рассмотрим первый цикл: ПОКА вверх понятно, что при движении вверх РОБОТ остановится в первой же клетке,
- 19. рассуждая аналогично, находим, что во втором цикле при движении вправо РОБОТ останавливается в клетке, где есть
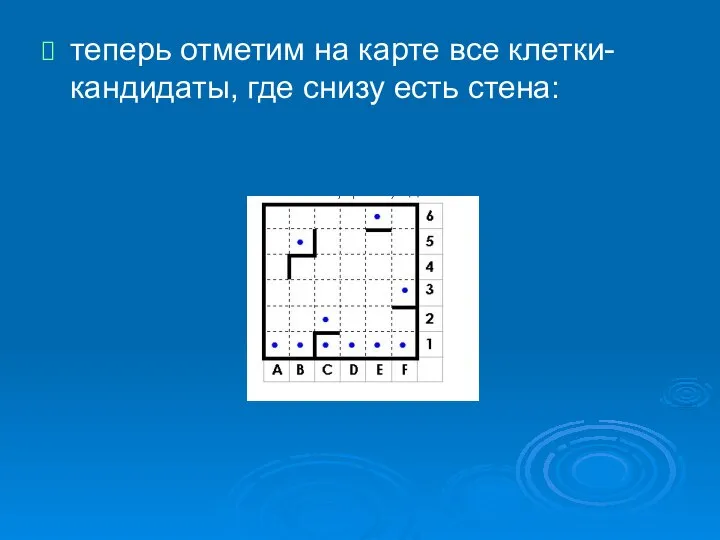
- 20. теперь отметим на карте все клетки-кандидаты, где снизу есть стена:
- 21. при движении из клеток B5, D1, E1, E6, F1 и F3 РОБОТ врежется в стенку, потому
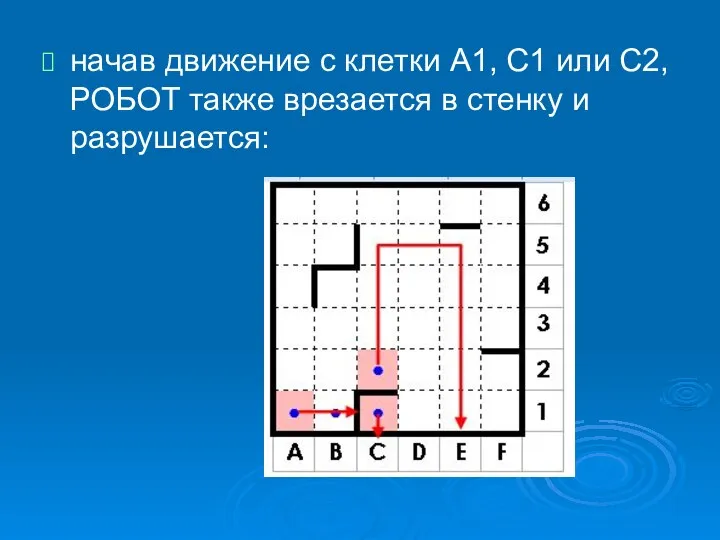
- 22. начав движение с клетки A1, C1 или C2, РОБОТ также врезается в стенку и разрушается:
- 24. Скачать презентацию








 Арбитраж. День 4
Арбитраж. День 4 Алгоритмический язык. Запись переменных и констант. 9-11 класс
Алгоритмический язык. Запись переменных и констант. 9-11 класс Архитектура ИС Лекция №5 BIOS
Архитектура ИС Лекция №5 BIOS Урок 1. Страхи и мотивация
Урок 1. Страхи и мотивация Проект. Система внутрикорпоративных коммуникаций (ВКК): диагностика и оптимизация
Проект. Система внутрикорпоративных коммуникаций (ВКК): диагностика и оптимизация Инструкция по созданию заявок. Форма для работы с отчетом
Инструкция по созданию заявок. Форма для работы с отчетом Гибридные криптосистемы защиты информации
Гибридные криптосистемы защиты информации Киберспорт
Киберспорт Базовые типы и операторы языка C#
Базовые типы и операторы языка C# Способы подключения к Интернету
Способы подключения к Интернету Десятичная система счисления
Десятичная система счисления Анализ уязвимостей драйверов
Анализ уязвимостей драйверов Журналистика Италии ХХ века
Журналистика Италии ХХ века Разработка СУБД для автоматизированной обработки статистических данных социологических опросов
Разработка СУБД для автоматизированной обработки статистических данных социологических опросов Спам и защита от него
Спам и защита от него Гиперссылки на Web-страницах. 11 класс
Гиперссылки на Web-страницах. 11 класс Работа над ошибками. Урок информатики
Работа над ошибками. Урок информатики SketchUp. Основы проектирования. Самый простой способ рисовать в 3D. Урок 4
SketchUp. Основы проектирования. Самый простой способ рисовать в 3D. Урок 4 Таблицы и картинки в документе Microsoft Word. Урок 9
Таблицы и картинки в документе Microsoft Word. Урок 9 Системы счисления
Системы счисления Binary Code
Binary Code Что такое цикл?
Что такое цикл? 10u-8_Python-I
10u-8_Python-I Educator Onlain. Воспитатель и его работа в период пандемии COVID-19
Educator Onlain. Воспитатель и его работа в период пандемии COVID-19 Информационное общество. Плюсы и минусы
Информационное общество. Плюсы и минусы ВК: продвижение страницы
ВК: продвижение страницы 1С:Университет ПРОФ. Общая информация о решении
1С:Университет ПРОФ. Общая информация о решении Разбор задач ЕГЭ. Кодирование чисел. Системы счисления. В7
Разбор задач ЕГЭ. Кодирование чисел. Системы счисления. В7