Слайд 2Метод Квайна
Способ представления функции в ДНФ или КНФ с минимальным количеством членов

и минимальным набором переменных.
Преобразование функции можно разделить на два этапа:
на первом этапе осуществляется переход от канонической формы (СДНФ или СКНФ) к так называемой сокращённой форме;
на втором этапе — переход от сокращённой формы к минимальной форме.
Слайд 3Первый этап (получение сокращённой формы)

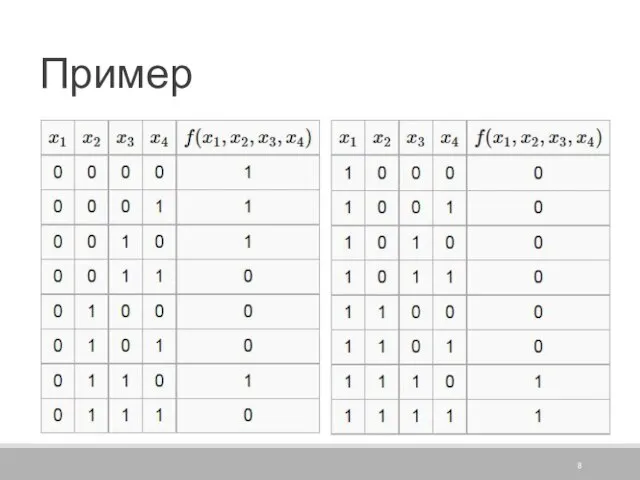
Слайд 5Пример
Пусть есть таблица истинности:

Слайд 7Второй этап (табличный)
Рассмотренный выше пример уже удовлетворяет определению минимальной формы, однако далеко

не всегда после первого этапа сокращённая форма совпадает с минимальной.
Ещё могут оставаться члены, чьё удаление не изменяет конечный результат.
На данном этапе требуется удалить лишние переменные.
Слайд 10Обработка импликантной матрицы
Мы вновь получили дизъюнкцию простых импликант, на этот раз в

количестве пяти штук.
Чтобы получить минимальную форму, воспользуемся импликантной матрицей.
Столбцы в ней соответствуют членам СДНФ, а строки — членам сокращённой формы.
Отмечаются столбцы членов СДНФ, которые поглощаются отдельными простыми импликантами:
Слайд 11Импликанты, не подлежащие исключению, образуют ядро.
Такие импликанты определяются по вышеуказанной матрице.
Для
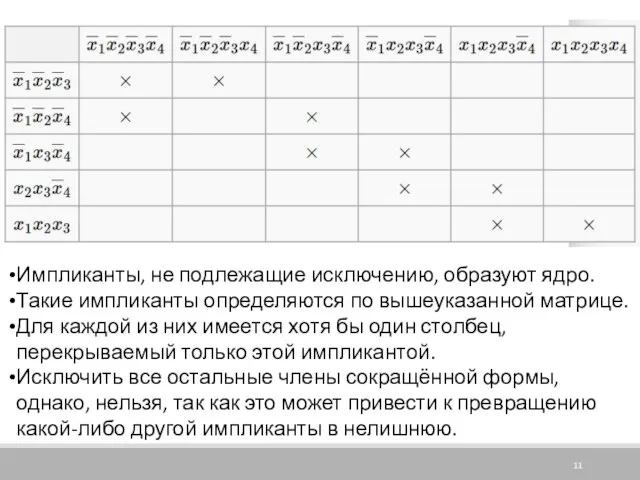
каждой из них имеется хотя бы один столбец, перекрываемый только этой импликантой.
Исключить все остальные члены сокращённой формы, однако, нельзя, так как это может привести к превращению какой-либо другой импликанты в нелишнюю.
Слайд 12Выбор остальных импликант, что войдут в минимальную форму, сводится к нахождению минимального

набора неядровых импликант, которые покроют столбцы, не перекрываемые ядровыми.
Применительно к рассматриваемому случаю это будут третий и четвёртый столбец.
То, что можно исключить остальные импликанты, легко проверяется. На соответствующих наборах мы получаем значение 1, которая получается и на удалённых импликантах.










 WEB 3.0
WEB 3.0 Программирование на языке PascalABC. Решение задач. Обмен значений
Программирование на языке PascalABC. Решение задач. Обмен значений Инициализация жесткого диска
Инициализация жесткого диска Школа для развития своего таланта. Проект
Школа для развития своего таланта. Проект Систематизация сбора и оценки работ учащихся
Систематизация сбора и оценки работ учащихся Winbox 1
Winbox 1 Разработка веб-приложения для автоматизации обработки данных тестирования учащихся
Разработка веб-приложения для автоматизации обработки данных тестирования учащихся Telegram-канал Табуретка
Telegram-канал Табуретка Знакомство с программой PowerPoint
Знакомство с программой PowerPoint Стилевое оформление текста
Стилевое оформление текста Amadeus Property Management System - крупнейшая дистрибьюторская система
Amadeus Property Management System - крупнейшая дистрибьюторская система Как стать самозанятым?
Как стать самозанятым? Машинное обучение на языке программирования Python
Машинное обучение на языке программирования Python Электронные ресурсы Вологодской ОУНБ в помощь генеалогическому поиску
Электронные ресурсы Вологодской ОУНБ в помощь генеалогическому поиску Вычислительная практика. Интерфейс
Вычислительная практика. Интерфейс Шкідливі програми
Шкідливі програми Демоны (Программы) Linux
Демоны (Программы) Linux Обработка потока данных. Цикл с параметром
Обработка потока данных. Цикл с параметром Программирование ветвлений. Основы программирования
Программирование ветвлений. Основы программирования Создание рабочего стола
Создание рабочего стола Загальне завдання. Створення документа
Загальне завдання. Створення документа Регистрация на Портале РКЦ
Регистрация на Портале РКЦ Безопасность в сети Интернет
Безопасность в сети Интернет Установка VRay
Установка VRay поколения ЭВМ
поколения ЭВМ Этические основы общения в Сети Интернет
Этические основы общения в Сети Интернет ЯПВУ. Лекция 1. Виды интерфейсов Windows
ЯПВУ. Лекция 1. Виды интерфейсов Windows іт гр 32 урок 2
іт гр 32 урок 2