Слайд 2Ограничения реляционной модели
Внутренние ограничения модели:
Неделимые (атомарные) значения
Каждая таблица должна иметь первичный ключ
Возможные

ключи
Нет дубликатов картежей (строк)
Домены (строковые, числовые и т.д.)
Явные ограничения
Описывают предметную область
Функциональные зависимости
Многозначные зависимости
Слайд 3Условные обозначения
А, В, С, ... — одиночные атрибуты,
X, Y, Z—множества атрибутов,

a, b, с, х, у, z — значения атрибутов.
Объединение множеств атрибутов, например, (А и У) — AY.
U, R, S — отношения.
Предположим, что существует универсальное отношение U, в схеме которого каждый атрибут имеет уникальное имя. Причем множество атрибутов любого другого отношения есть некоторое подмножество атрибутов схемы отношения U.
Слайд 4Функциональная зависимость
Пусть X и Y — атрибуты отношения R.
Атрибут Y отношения

R функционально зависит от атрибута X отношения R, если в каждый момент времени каждому значению х соответствует одно и то же значение у.
Функциональная зависимость f атрибута X от атрибута Y такова:
Слайд 5Свойства ФЗ
Обозначение Х ≠ У показывает, что между X и Y нет

функциональной зависимости.
Если А—>У и У—>А, то между A и Y существует взаимно однозначное соответствие.
Слайд 6Пример функциональной зависимости
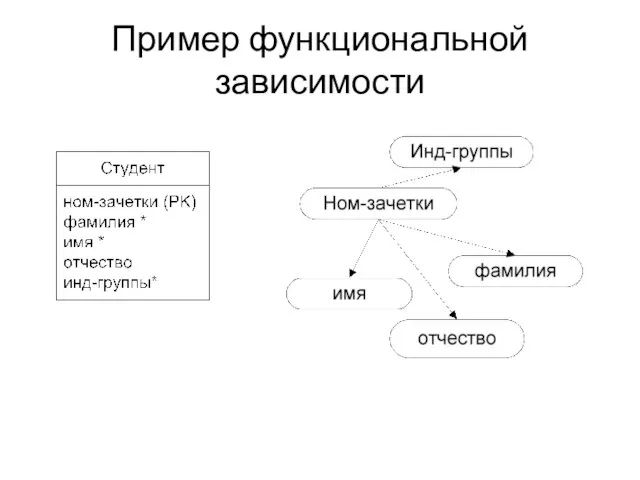
Слайд 7Описание ФЗ на примере
На отношении R(A1,A2,...An) определено множество функциональных зависимостей F =

{ A1->A2, A1->A3, ..... }
На отношении
Студент(ном-зачетки, фамилия, имя, отчество, инд-группы)
определено мн-во ФЗ
F = { Ном-зачетки-> Фамилия, Ном-зачетки->Имя, Ном-зачетки->Отчество,Ном-зачетки-> Инд-группы}
Слайд 8Многозначные зависимости
Многозначная зависимость m У от X:
m: X →→ Y.
Многозначная зависимость существует,

если при заданных значениях атрибутов из X существует множество, состоящее из нуля или более взаимосвязанных значений атрибутов из У,
причем множество значений У не связано со значениями атрибутов в от ношении «R—X—У», где R — все множество атрибутов отношения.
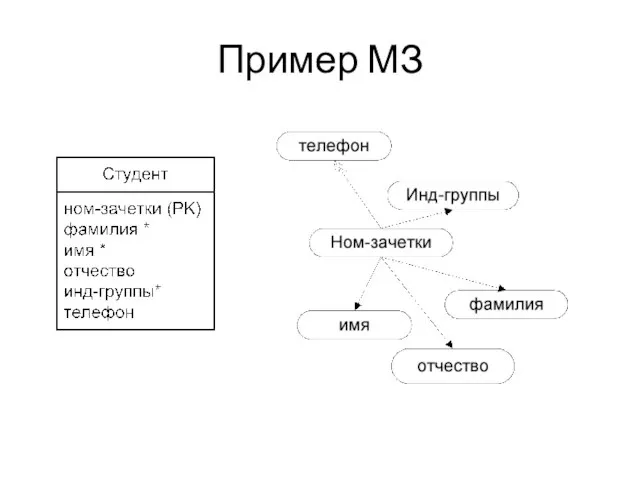
Слайд 10Описание МЗ в примере
На отношении R(A1,A2,...An) определено множество функциональных и многозначных зависимостей

F = { A1->A2, A1->A3, ..... A1->->An }
На отношении
Студент(ном-зачетки, фамилия, имя, отчество, инд-группы)
определено мн-во ФЗ
F = { Ном-зачетки-> Фамилия, Ном-зачетки->Имя, Ном-зачетки->Отчество,Ном-зачетки-> Инд-группы, Ном-зачетки->-> Телефон}
Слайд 11Проверка наличия МЗ в отношении
Если в R имеет место зависимость X->->Y, то

для двух произвольных кортежей t и s, таких, что t[X] = s[X] (т. е. t и s совпадают по значениям атрибутов X), отношение обязательно содержит кортежи u и v, такие, что выполняются условия:
u[X] = v[X] = t[X] = s[X]
u[Y] = t[Y]
u[R-X-Y] = s[R-X-Y]
v[Y] = s[Y]
v[R-X-Y] = t[R-X-Y]
Если поменять местами значения атрибутов У в кортежах t и s, то можно получить два кортежа u и v, которые также должны, принадлежать рассматриваемому отношению.
Слайд 141-ая нормальная форма (1ПФ)
Схема отношения R находится в первой нормальной форме тогда

и только тогда, когда все входящие в нее атрибуты являются атомарными
т. е. значения соответствующих доменов рассматриваются как неделимые, а не как множества или кортежи из более элементарных доменов.
Слайд 152-ая нормальная форма (2НФ)
Схема отношения R находится во второй нормальной форме, если

она находится в 1НФ и каждый ее непервичный атрибут функционально полно зависит от первичного ключа.
Слайд 16Свойство 2НФ
Если X — ключ отношения R, Y≤X,
А — непервичный (неключевой)

атрибут отношения R,
то в отношении R имеет место частичная зависимость (неполная функциональная зависимость), когда
Х->А и Y->A.
Если это условие не выполняется, то атрибут А функционально полно зависит от X в отношении R.
Отношение, находящееся во 2НФ может обладать аномалиями для выполнения операций включения, удаления и модификации.
Слайд 17Пример 2НФ
Исходное отношение R(A1,A2,A3,A 4, A5) – нарушает 2НФ
Результат декомпозиции исходного отношения:
R1(A1,A2,A3,
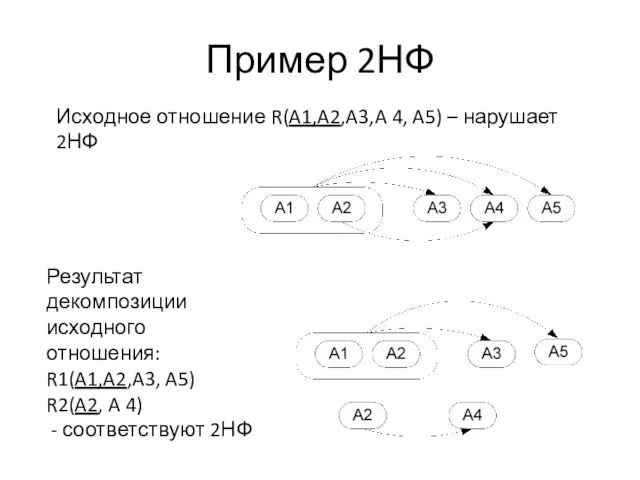
A5)
R2(A2, A 4)
- соответствуют 2НФ
Слайд 183-ая нормальная форма (3НФ)
Схема отношения R находится в третьей нормальной форме, если

не существует ключа X для R, множества атрибутов Y ≤ R и непервичного атрибута А из R, таких, что:
X—>Y справедливо в R,
У—>А справедливо в R, но Y—>X не имеет места.
Схема отношения R находится в третьей нормальной форме, если она находится в 2НФ и каждый непервичный атрибут нетранзитивно зависит от первичного ключа.
Слайд 19Пример 3НФ
Исходное отношение R(A1,A2,A3,A4 , A5)- нарушает 3НФ
Р езультат декомпозиции исходного отношения:
R1(A1,A2,A3,
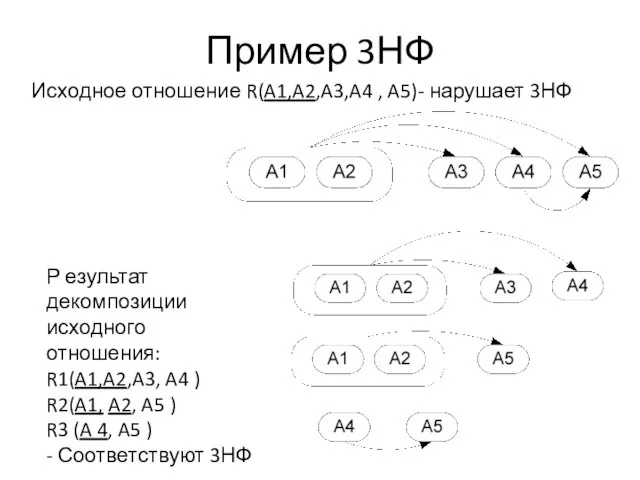
A4 )
R2(A1, A2, A5 )
R3 (A 4, A5 )
- Соответствуют 3НФ
Слайд 20Свойство 3НФ
Когда отношение имеет только один ключ и другие зависимости, в том

числе многозначные, в нем отсутствуют, то ЗНФ освобождает от избыточности и аномалий выполнения операций включения, удаления и модификации.
Если в отношении, находящемся в ЗНФ, отсутствуют многозначные зависимости, но имеются другие зависимости, кроме зависимости от ключа, то ЗНФ будет иметь аномалии операций.
В этом случае рассматривают усиленную третью нормальную форму (нормальная форма Бойса —Кодда).
Слайд 213-ая усиленная нормальная форма (НФ Бойса-Кодда)
Схема отношения R с зависимостями F находится

в усиленной третьей нормальной форме, если всякий раз, когда в R имеет место зависимость Х −> А и A не принадлежит X, то X является возможным ключом отношения R.
Атрибут (или комбинацию атрибутов), от которого какой-либо другой атрибут зависит функционально (полно), называют детерминантой.
В этом случае нормализованная схема отношения R находится в усиленной третьей нормальной форме, если каждая детерминанта является возможным ключом.
Если в отношении отсутствуют многозначные зависимости, то снимаются все аномалии операций включения, удаления и модификации.
Слайд 22Пример НФБК
Исходное отношение R(A1,A2,A3,A 4 , A5) - нарушает НФБД
Детерминанты
A1 и A3
Р
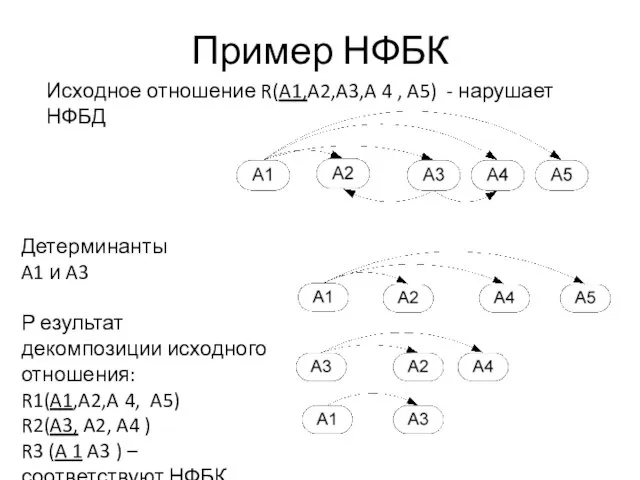
езультат декомпозиции исходного отношения:
R1(A1,A2,A 4, A5)
R2(A3, A2, A4 )
R3 (A 1 A3 ) – соответствуют НФБК
Слайд 234 -ая нормальная форма (4 НФ)
Если в отношении присутствуют многозначные зависимости, то

схема отношения должна находиться в четвертой нормальной форме. В противном случае снова возникнут соответствующие аномалии.
Схема отношения R будет находиться в четвертой нормальной форме, если всякий раз, когда существует многозначная зависимость X—> —> У (где У — не пустое множество и не является подмножеством X и XY состоит не из всех атрибутов R), также существует зависимость Х —> А для любого атрибута А в R.
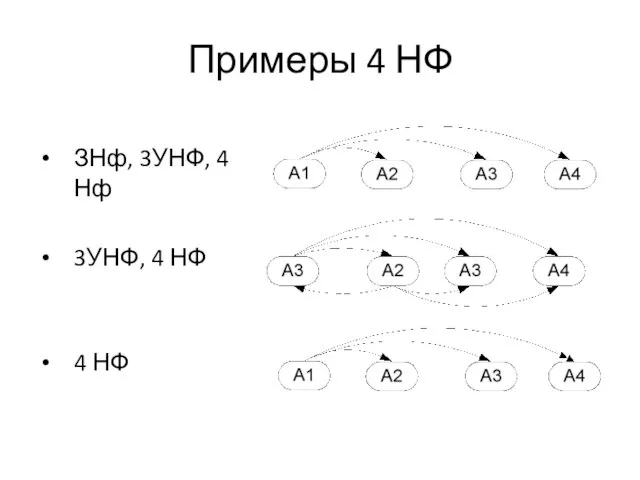
Слайд 24Примеры 4 НФ
ЗНф, 3УНФ, 4 Нф
3УНФ, 4 НФ
4 НФ
Слайд 25Аномалии
Сложность выполнения операций
Отсутствуют при чтении
Встречаются при добавлении, удалении, изменении
Дубликаты, повтор действий, удаление

данных
Персона (ФИО, телефон, почта, организация, раб.телефон, адр.орг, должность)
При удалении персоны удалятся сведения об организации
При обновлении данных организации надо изменять всех персон
Дублируются сведения об организации
Нельзя добавить сведения об организации без персоны
Персона (ФИО, телефон, почта, организация, должность)
Организация(название, раб.телефон, адрес)
Аномалии отсутствуют
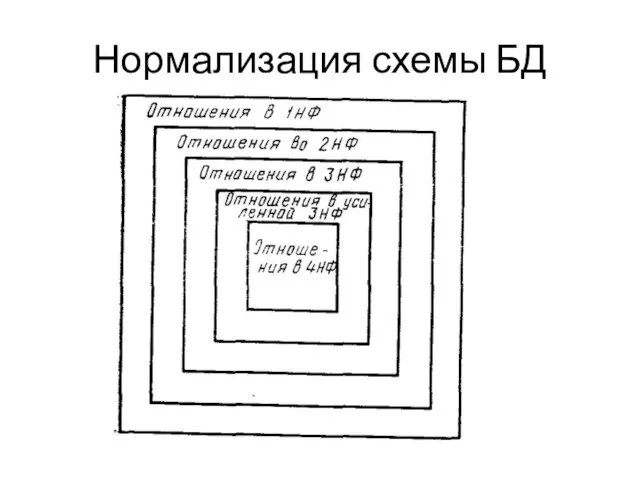
Слайд 26Нормализация
Нормализация отношений выполняется декомпозицией их схем.
Декомпозицией схемы отношения R={A1 А2,..., Ап} называется

замена схемы совокупностью схем р= {Ri, R2, ..., Rn} подмножеств, таких, что
Ri U Rz U ... URk = R= {А1, А2,..., Аn}.
При этом не требуется, чтобы схемы Rt были непересекающимися.
Однако не все докомпозиции могут обладать свойством соединения без потерь (если естественное соединение не восстанавливает первоначальное отношение, то нет способа, выполняющего его однозначное восстановление) и свойством сохранения зависимостей.
Слайд 28Решение
R1 (A1, A2,A3, A 4, A6, A12 )
R2( A 4 , A5

)
R3 (A5, A9, A1 0 , A11 )
R 4 (A6, A 7 )
R5 ( A7 , A8)
R6 (A13, A12, A14 )
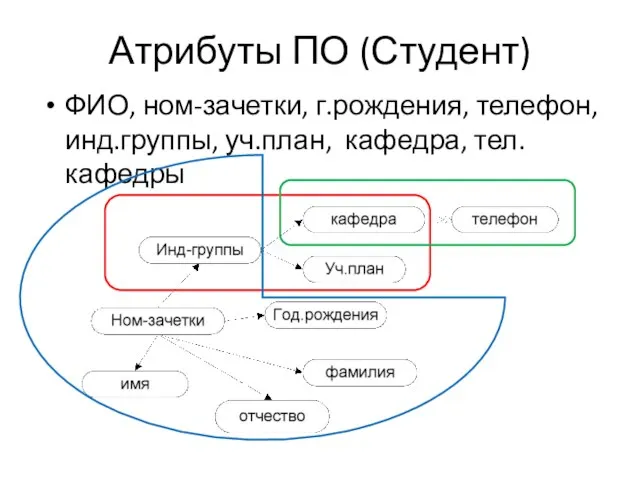
Слайд 29Атрибуты ПО (Студент)
ФИО, ном-зачетки, г.рождения, телефон, инд.группы, уч.план, кафедра, тел.кафедры
Слайд 30Схема БД Студента (4 НФ)
Студент ( Ном-зачетки, Фамилия, Имя, Отчество, год.рождения, Инд-кафедры

)
Группа( инд-группы, Уч.план, Кафедра )
Кафедра(кафедра, телефон)


























 Информационные технологии
Информационные технологии Кроссворд
Кроссворд Презентация на тему Жесткий диск
Презентация на тему Жесткий диск  Алгоритм установления соединения в сети IP-телефонии по протоколу SIP
Алгоритм установления соединения в сети IP-телефонии по протоколу SIP Объектно-ориентированное программирование
Объектно-ориентированное программирование Возможные применения теории фракталов в криптографии
Возможные применения теории фракталов в криптографии Основы работы с регулярными выражениями и производство http запросов. Библиотека регулярных выражений re
Основы работы с регулярными выражениями и производство http запросов. Библиотека регулярных выражений re Анимация. Подводный мир
Анимация. Подводный мир Информационная безопасность: mr. Robot в реалиях российского университета
Информационная безопасность: mr. Robot в реалиях российского университета Работа с базой данных
Работа с базой данных 01_10_2022_EII
01_10_2022_EII Логика. Понятие
Логика. Понятие Разработка программ обработки одномерных массивов
Разработка программ обработки одномерных массивов Физическая культура и спорт. Начать тестирование
Физическая культура и спорт. Начать тестирование Презентация на тему Рекомендации по проведению ГИА по информатике и ИКТ
Презентация на тему Рекомендации по проведению ГИА по информатике и ИКТ  Создание многоуровневого списка Учитель информатики МАОУ "СОШ №55" г. Пермь Бадьина Лариса Ивановна
Создание многоуровневого списка Учитель информатики МАОУ "СОШ №55" г. Пермь Бадьина Лариса Ивановна CSS (Cascading Style Sheets)
CSS (Cascading Style Sheets) Парcер всех объявлений Yad2.co.il
Парcер всех объявлений Yad2.co.il Технологии программирования
Технологии программирования WinUI. The modern native Ul platform of Windows
WinUI. The modern native Ul platform of Windows Презентация по информатике на тему _Перевод чисел из одной системы счисления в другую_
Презентация по информатике на тему _Перевод чисел из одной системы счисления в другую_ Презентация на тему Интернет: да или нет
Презентация на тему Интернет: да или нет  Data Quality DWBI Test Plan and Test Strategy
Data Quality DWBI Test Plan and Test Strategy Автокодировщики. RNN, GANs
Автокодировщики. RNN, GANs Как написать и выложить новость на платформу
Как написать и выложить новость на платформу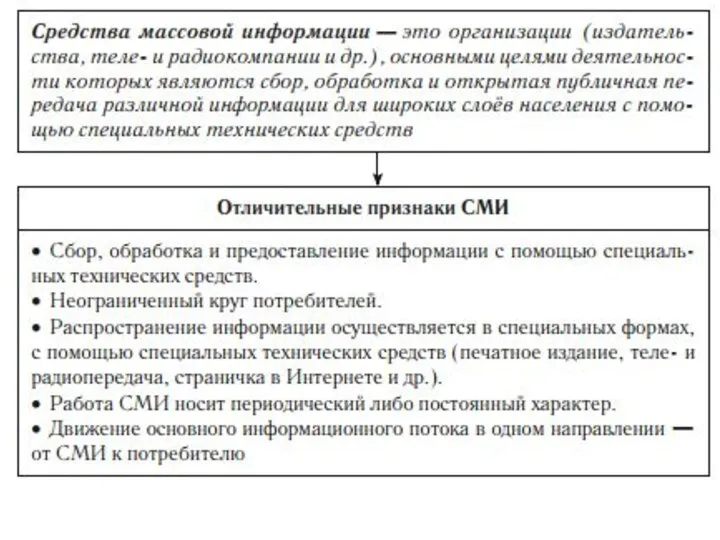 Средства массовой информации
Средства массовой информации Программирование на языке C++
Программирование на языке C++ Компьютерная графика и анимация. Фракталы
Компьютерная графика и анимация. Фракталы