понятие — эффективность алгоритма.
Функция сложности (О) выражает относительную скорость алгоритма в зависимости от некоторой переменной (переменных). Существуют три важных правила для определения функции сложности.
1. 0(kf) = Oif). Здесь к обозначает константу, а/— функция. Это правило декларирует, что постоянные множители не имеют значения для определения порядка сложности, например, О (1,5-TV) = О (N).
2. 0(fg) = 0(f) • 0(g) или 0(f/g) = 0(f)/0(g). Здесь/и g — функции. Из этого правила следует, что порядок сложности произведения двух функций равен произведению их сложностей, например, 0{{ 11-N) ? N) = 0{ 11-N) O(N) = 0(N) • O(N) = O(NN) = 0(N2).
3. Oif + g) равна доминанте 0(f) и 0(g). Из этого правила следует, что порядок сложности суммы функций определяется как порядок доминанты первого и второго слагаемых, т.е. выбирается наибольший порядок, например, 0(N5 + N2) = 0(№).
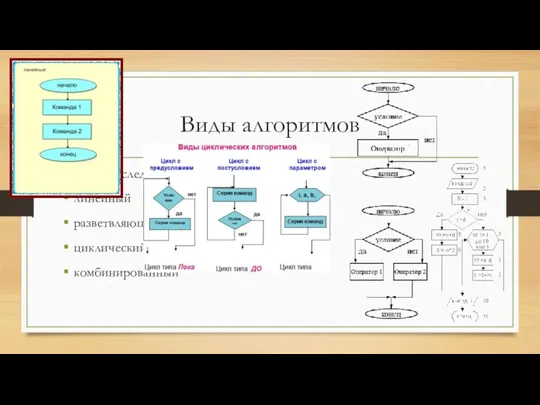


 FDDI - наиболее подходящая технология для оптоволоконного кабеля
FDDI - наиболее подходящая технология для оптоволоконного кабеля Центр цифровых образовательных технологий
Центр цифровых образовательных технологий Построить блок-схему и написать программу
Построить блок-схему и написать программу Деление и обобщение понятий. (4 класс)
Деление и обобщение понятий. (4 класс) Название и интерфейс MS EXCEL
Название и интерфейс MS EXCEL Технология создания виртуальной выставки
Технология создания виртуальной выставки 3
3 Передача и коммутация данных в компьютерных сетях. Часть 1. Лекция 3
Передача и коммутация данных в компьютерных сетях. Часть 1. Лекция 3 Сайт для голосований “Simple votings”
Сайт для голосований “Simple votings” CSS (каскадные документы стилей)
CSS (каскадные документы стилей) Новые возможности партнёрства по проекту “Календарь” [для автокурьеров с Андроидом]
Новые возможности партнёрства по проекту “Календарь” [для автокурьеров с Андроидом] Презентация на тему Алгоритмы сжатия. Алгоритм построения орграфа Хаффмана
Презентация на тему Алгоритмы сжатия. Алгоритм построения орграфа Хаффмана  21-22_Объект события
21-22_Объект события Электронный журнал в Exsel Шаг 1 Рисуем журнал Презентация была создана по просьбе коллег Автор: Сомова С.Г. МБОУ СОШ г. Багратионов
Электронный журнал в Exsel Шаг 1 Рисуем журнал Презентация была создана по просьбе коллег Автор: Сомова С.Г. МБОУ СОШ г. Багратионов Методика определения возможного ущерба и алгоритма определения уровня защищённости государственных информационных систем
Методика определения возможного ущерба и алгоритма определения уровня защищённости государственных информационных систем Урок 2. Услуги персонального стилиста. Продуктовая линейка
Урок 2. Услуги персонального стилиста. Продуктовая линейка Проект Цифровая платформа МАИ
Проект Цифровая платформа МАИ Рекурсия. Картинка
Рекурсия. Картинка Вводная презентация
Вводная презентация Красная звезда. №136
Красная звезда. №136 Характеристики модели паруса. алгоритм ее создания
Характеристики модели паруса. алгоритм ее создания Python 6.0.2022_ООП
Python 6.0.2022_ООП Создание веб-сайтов
Создание веб-сайтов Уро13_Адаптивная верстка
Уро13_Адаптивная верстка CryptoHands. Первый абсолютно Безрисковый блокчейн проект!
CryptoHands. Первый абсолютно Безрисковый блокчейн проект! Prezentācija par vīrusiem un antivīrusu programmām
Prezentācija par vīrusiem un antivīrusu programmām Услуги по продвижению в социальных сетях
Услуги по продвижению в социальных сетях Математическая логика (булева алгебра)
Математическая логика (булева алгебра)