PnP Perspective-n-Point. Восстановление точек в 3D-пространстве по их перспективной проекции на плоскость сенсора камеры

ОПРЕДЕЛЕНИЕ
ЗАДАЧА PnP – восстановление точек в 3D-пространстве по их перспективной проекции на плоскость сенсора камеры.

СУТЬ
Априорно известны:
Rij (то есть геометрия тела)
Коэффициенты дисторсии
Матрица внутренних параметров камеры
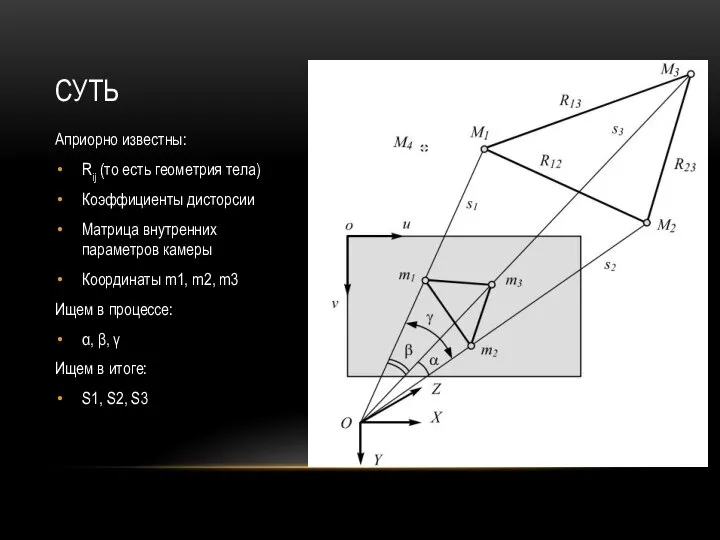
Координаты m1, m2, m3
Ищем в процессе:
α, β, γ
Ищем в итоге:
S1, S2, S3

МАТЕМАТИКА P3P
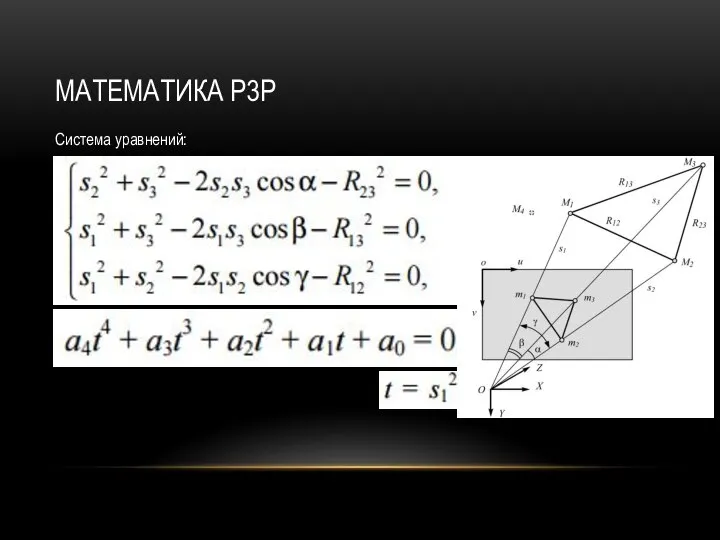
Система уравнений:

ПРОБЛЕМЫ P3P

ОДНОЗНАЧНОЕ РЕШЕНИЕ ДАЕТСЯ ПРИ N≥4

РЕШЕНИЕ В OPENCV

АЛГОРИТМЫ
SOLVEPNP_ITERATIVE // На базе метода Левенберга-Марквардта
SOLVEPNP_P3P // В действительности используется 4 точки*
SOLVEPNP_EPNP // Efficient Perspective-n-Point
SOLVEPNP_DLS // A Direct Least-Squares
SOLVEPNP_UPNP // Uncalibrated PnP, "Exhaustive Linearization for Robust Camera Pose and Focal Length Estimation"
* - http://docs.opencv.org/3.1.0/d9/d0c/group__calib3d.html#ga549c2075fac14829ff4a58bc931c033d

EPNP

RANSAC (БОЛЕЕ УСТОЙЧИВОЕ К ВЫБРОСАМ)

О МЕТОДАХ:
DLT - direct linear transformation method
EPnP - efficient O(n) non-iterative solution of PnP
EPnP+GN - the EPnP method followed with a Gaussian-Newton optimizer
LHM - Lu et al method
HOMO - the homography method for planar targets

ПРИМЕР РЕШЕНИЯ ЗАДАЧИ PNP