Содержание
- 2. Высказывания и операции над ними
- 3. Определение Под высказыванием понимают языковое предложение, о котором можно сказать, истинно оно или ложно
- 4. Логические значения высказываний: «истина» (И, 1, t) «ложь» (Л, 0, f)
- 5. Примеры: Париж – столица Англии Шесть делится на два Сколько будет 7*7? 7 * х =
- 6. Высказывание, представляющее собой одно утверждение, называют простым (элементарным). Высказывания, которые получаются из простых с помощью грамматических
- 7. Пример Карась не рыба Это простое или сложное высказывание?
- 8. Все высказывания будем рассматривать с точностью до их логического значения Пример «В Красноярске есть педагогический вуз»
- 9. Элементарные высказывания будем обозначать латинскими буквами: А, В, С, … x, y, z, ...
- 10. Логическое значение высказывания определяется функцией истинности, которая принимает значения в двухэлементном множестве {0; 1}
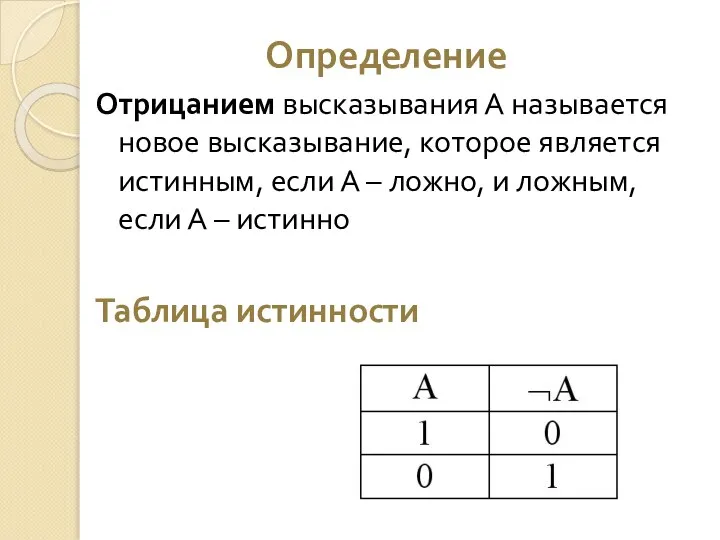
- 11. Определение Отрицанием высказывания А называется новое высказывание, которое является истинным, если А – ложно, и ложным,
- 12. Определение Отрицанием высказывания А называется новое высказывание, которое является истинным, если А – ложно, и ложным,
- 13. Определение Конъюнкцией двух высказываний А, В называется новое высказывание, которое является истинным в единственном случае, если
- 14. Определение Конъюнкцией двух высказываний А, В называется новое высказывание, которое является истинным в единственном случае, если
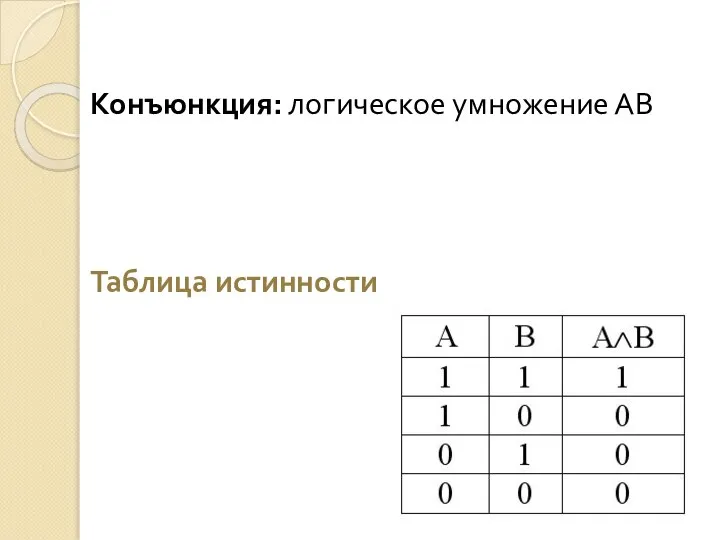
- 15. Конъюнкция: логическое умножение АВ Таблица истинности
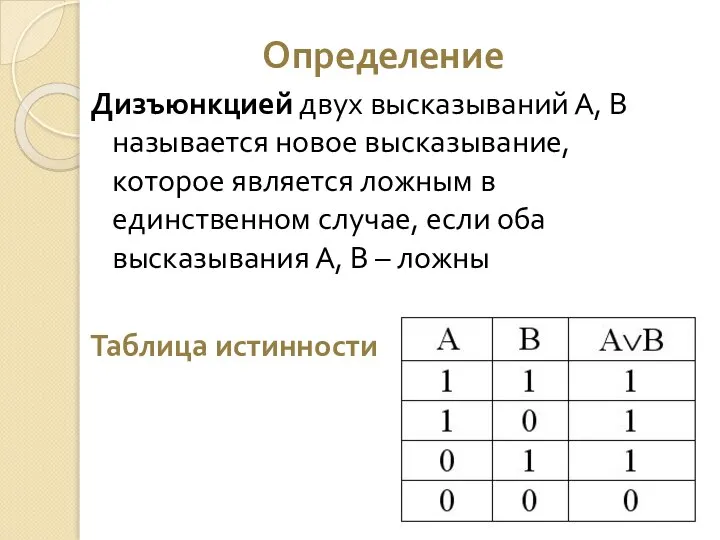
- 16. Определение Дизъюнкцией двух высказываний А, В называется новое высказывание, которое является ложным в единственном случае, если
- 17. Определение Дизъюнкцией двух высказываний А, В называется новое высказывание, которое является ложным в единственном случае, если
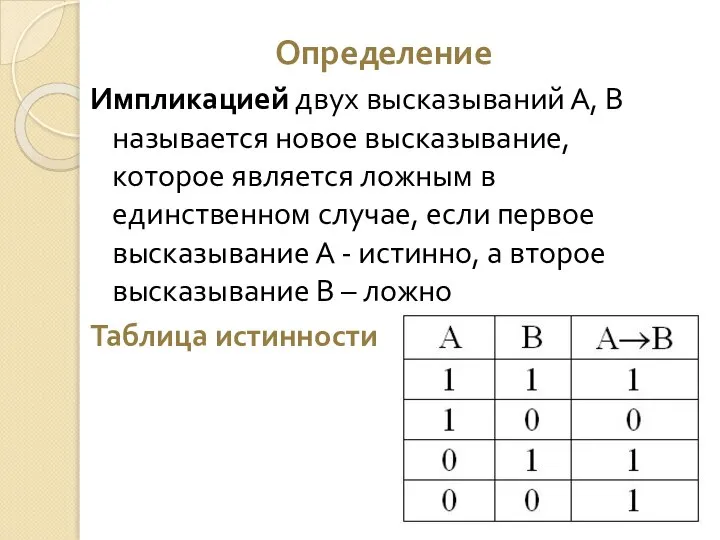
- 18. Определение Импликацией двух высказываний А, В называется новое высказывание, которое является ложным в единственном случае, если
- 19. Импликация Обозначение: Читается: «если А, то В» «из А следует В» «А имплицирует В» А –
- 20. Определение Импликацией двух высказываний А, В называется новое высказывание, которое является ложным в единственном случае, если
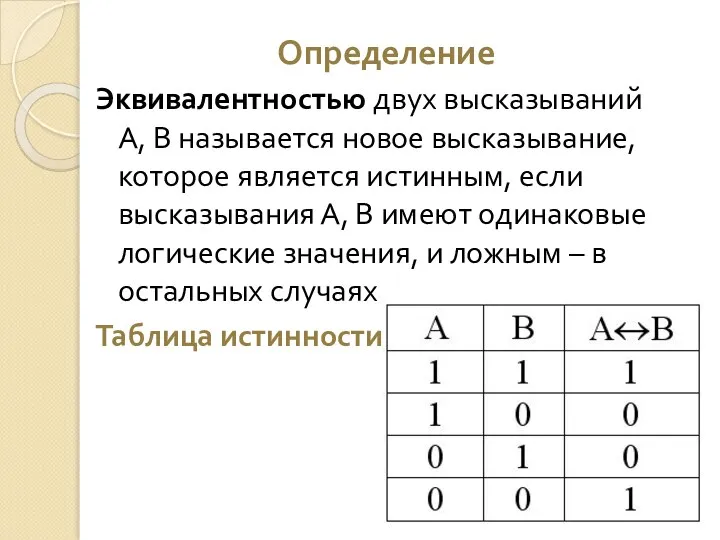
- 21. Определение Эквивалентностью двух высказываний А, В называется новое высказывание, которое является истинным, если высказывания А, В
- 22. Эквивалентность Обозначение: A~B, Читается: - «А тогда и только тогда, когда В» - «для того, чтобы
- 23. Определение Эквивалентностью двух высказываний А, В называется новое высказывание, которое является истинным, если высказывания А, В
- 24. Разделительное «или» Обозначение: Читается: «А не эквивалентно В» Операция “XOR”
- 25. Определение Разделительное «или» для двух высказываний А, В это новое высказывание, которое истинно, если высказывания А,
- 26. Дополнительные связки
- 27. Таблицы истинности Составляются для любой формулы логики высказываний Если в формуле n переменных, то в таблице
- 28. Для формулы, которая содержит две переменные, таких наборов значений переменных всего четыре: (0,0), (0,1), (1,0), (1,1).
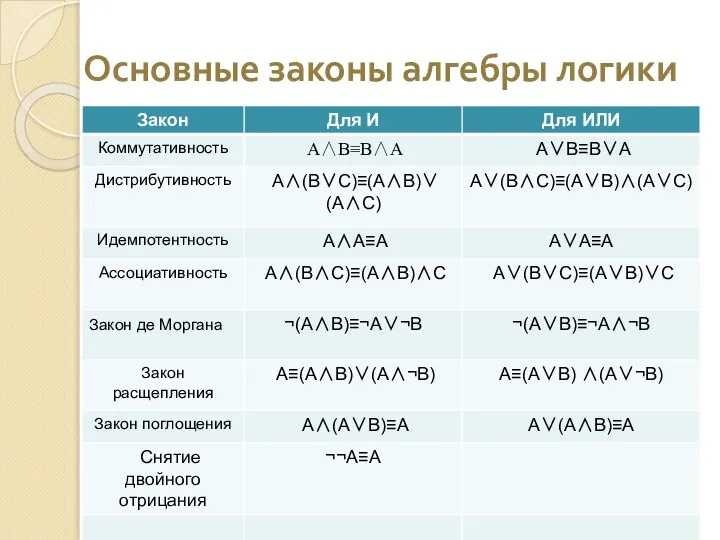
- 29. Основные законы алгебры логики
- 30. Выражение одних логических связок через другие: А⊃В≡¬А∨В≡¬(А∧¬В) А~В≡(А⊃В)∧(В⊃А)≡(¬A∨B)∧(¬B∨A) ≡ (А∧В)∨(¬А∧¬В) А∨В≡¬А⊃В≡¬(¬А∧¬В) А∧В≡¬(А⊃¬В)≡(¬(¬А∨¬В)) А В≡ ¬ (А~В)
- 31. Тавтология Некоторые формулы принимают значение “истина” при любых значениях истинности входящих в них переменных. Например, формула
- 32. Тождественная ложь В качестве другого примера рассмотрим формулу А & , которой соответствует, например, высказывание “Катя
- 33. Тождественная ложь При всех наборах значений переменных x и y формула принимает значение 0, то есть
- 35. Скачать презентацию


























 Microsoft Office. Краткая характеристика программ офисного пакета
Microsoft Office. Краткая характеристика программ офисного пакета Виды компьютерных сетей
Виды компьютерных сетей Аналитика BLS
Аналитика BLS Система AutoFix13
Система AutoFix13 Использование ИКТ (информационно-коммуникативных технологий) на уроках физической культуры
Использование ИКТ (информационно-коммуникативных технологий) на уроках физической культуры Ур. 2 Информация и ее свойства
Ур. 2 Информация и ее свойства Программное обеспечение (ПО) компьютера
Программное обеспечение (ПО) компьютера Неиерархические сети
Неиерархические сети Форум абитуриентов ДонНУЭТ-2021 г
Форум абитуриентов ДонНУЭТ-2021 г ВКР: Разработка проекта по использованию туннелей для сети предприятия с целью защиты информации для ООО “Бут Групп”
ВКР: Разработка проекта по использованию туннелей для сети предприятия с целью защиты информации для ООО “Бут Групп” Clover Platform. Назначение и основные функции платформы
Clover Platform. Назначение и основные функции платформы Аналоговое и цифровое представление величин
Аналоговое и цифровое представление величин Проект онлайн турнира по CS:GO “Cyber stalker”
Проект онлайн турнира по CS:GO “Cyber stalker” Cацыяльныя сеткi “за”
Cацыяльныя сеткi “за” Текстовый процессор Writer
Текстовый процессор Writer Тексты в компьютерной памяти
Тексты в компьютерной памяти Обеспечение информационной безопасности детства
Обеспечение информационной безопасности детства Устройство компьютера
Устройство компьютера Работа с файлами
Работа с файлами Творческая работа на уроке информатики
Творческая работа на уроке информатики Информация о переподключении к веб-сервису Росреестра
Информация о переподключении к веб-сервису Росреестра Интерактивная система помощи иностранным студентам
Интерактивная система помощи иностранным студентам Защищенные операционные системы
Защищенные операционные системы The Information-Action Value Chain
The Information-Action Value Chain Обучение ООП с помощью видеоигры
Обучение ООП с помощью видеоигры Трояны. Программы-шпионы
Трояны. Программы-шпионы Информационная безопасность
Информационная безопасность Мобильный медиаплеер
Мобильный медиаплеер