- Главная
- Информатика
- Практическая работа. Excel

Содержание
- 2. Решение Запускаем процессор Excel . В произвольно выбранной ячейке открывшегося «Листа» программы с адресом ячейки, например,
- 3. Вычислительная машина может строить график функции, если известен шаг изменения значений аргумента функции, поэтому его надо
- 4. Аналогично пункту 6 протягиваем указатель мыши по ячейкам таблицы со значениями до конца таблицы по .
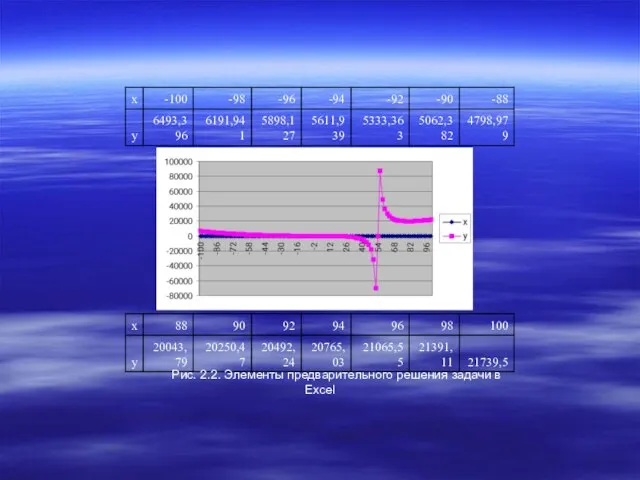
- 5. Рис. 2.2. Элементы предварительного решения задачи в Excel
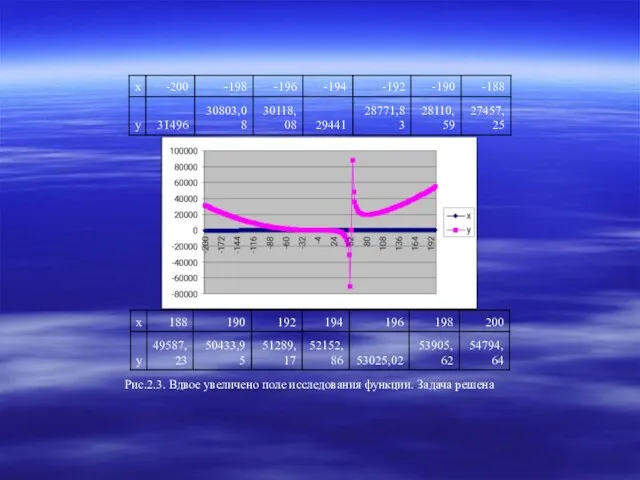
- 6. Рис.2.3. Вдвое увеличено поле исследования функции. Задача решена
- 7. Если вид графика не позволяет определенно судить о характере изменения функции во всём диапазоне изменения аргумента,
- 9. Скачать презентацию
Слайд 2Решение
Запускаем процессор Excel .
В произвольно выбранной ячейке открывшегося «Листа» программы с адресом
Решение
Запускаем процессор Excel .
В произвольно выбранной ячейке открывшегося «Листа» программы с адресом

ячейки, например, U19, набираем с клавиатуры величину аргумента . Язык клавиатуры английский. Поиск ячейки с указанным адресом осуществляется с помощью нижней линейки прокрутки.
В ближайшей по горизонтали (в этом варианте далее будем строить вертикальную таблицу числовых значений и ) или по вертикали (в этом варианте далее будет строиться горизонтальная таблица соответствия числовых значений и ) ячейке набираем величину функции . Пусть это будет ячейка U20. Здесь следует иметь в виду, что размер электронной таблицы на «Листе» ограничен её 256 столбцами и 16384 строками.
В первой соседней ячейке таблицы, следующей за ячейкой с аргументом , набираем первое (начальное) число из диапазона рассматриваемых значений . Пусть оно будет равно «-100». Адрес ячейки V19. Понятно, что таблица строится горизонтальная.
В ближайшей по горизонтали (в этом варианте далее будем строить вертикальную таблицу числовых значений и ) или по вертикали (в этом варианте далее будет строиться горизонтальная таблица соответствия числовых значений и ) ячейке набираем величину функции . Пусть это будет ячейка U20. Здесь следует иметь в виду, что размер электронной таблицы на «Листе» ограничен её 256 столбцами и 16384 строками.
В первой соседней ячейке таблицы, следующей за ячейкой с аргументом , набираем первое (начальное) число из диапазона рассматриваемых значений . Пусть оно будет равно «-100». Адрес ячейки V19. Понятно, что таблица строится горизонтальная.
Слайд 3Вычислительная машина может строить график функции, если известен шаг изменения значений аргумента
Вычислительная машина может строить график функции, если известен шаг изменения значений аргумента

функции, поэтому его надо машине задать. В следующую вторую ячейку таблицы вводим, как и прежде, с клавиатуры, второе по ходу изменения аргумента его числовое значение. Если величина шага по выбрана равной, например, «2», то второе число равно «-98».
Выбираем последнее (конечное) число из диапазона рассматриваемых значений . Пусть оно будет равно «+100». Надо заполнить оставшиеся 99 ячеек таблицы с числовыми значениями от «–96» до «+100» с шагом «2». Это, конечно, можно сделать и вручную, однако технологичнее использовать возможности компьютерной инструментальной программы. Выделяем ячейки с числами «–100» и «–98»: наводим указатель мыши на ячейку с числом «–100», нажимаем левую кнопку мыши и не отпуская её, переводим указатель мыши на ячейку с числом «–98». Отпускаем левую кнопку мыши: обе ячейки на экране монитора выделены линией и цветом, и в их правом нижнем углу появился маркер (выделенная точка). Наводим указатель мыши на маркер, нажимаем левую кнопку мыши и, не отпуская её, протягиваем курсор до ячейки с числом «100», которое появится в процессе перебора чисел от «–96» до «100» в выпадающем указателе снизу от рассматриваемой ячейки. Отпускаем левую кнопку мыши. Адрес последней правой ячейки с числом «100» есть DR19. ЭВМ готова автоматически перебирать значения по от «–100» до «+100» с шагом «2» /10/.
В первой следующей за ячейкой с аргументом соседней ячейке таблицы с адресом V20 набираем выражение функции в одну строку: «=(U19^3+17)/(U19-54)». Командой «Ввести» (нажатие клавиши “Enter”) вызывается появление в этой ячейке значения функции = 6493,396, соответствующего значению аргумента = -100.
Выбираем последнее (конечное) число из диапазона рассматриваемых значений . Пусть оно будет равно «+100». Надо заполнить оставшиеся 99 ячеек таблицы с числовыми значениями от «–96» до «+100» с шагом «2». Это, конечно, можно сделать и вручную, однако технологичнее использовать возможности компьютерной инструментальной программы. Выделяем ячейки с числами «–100» и «–98»: наводим указатель мыши на ячейку с числом «–100», нажимаем левую кнопку мыши и не отпуская её, переводим указатель мыши на ячейку с числом «–98». Отпускаем левую кнопку мыши: обе ячейки на экране монитора выделены линией и цветом, и в их правом нижнем углу появился маркер (выделенная точка). Наводим указатель мыши на маркер, нажимаем левую кнопку мыши и, не отпуская её, протягиваем курсор до ячейки с числом «100», которое появится в процессе перебора чисел от «–96» до «100» в выпадающем указателе снизу от рассматриваемой ячейки. Отпускаем левую кнопку мыши. Адрес последней правой ячейки с числом «100» есть DR19. ЭВМ готова автоматически перебирать значения по от «–100» до «+100» с шагом «2» /10/.
В первой следующей за ячейкой с аргументом соседней ячейке таблицы с адресом V20 набираем выражение функции в одну строку: «=(U19^3+17)/(U19-54)». Командой «Ввести» (нажатие клавиши “Enter”) вызывается появление в этой ячейке значения функции = 6493,396, соответствующего значению аргумента = -100.
Слайд 4Аналогично пункту 6 протягиваем указатель мыши по ячейкам таблицы со значениями до
Аналогично пункту 6 протягиваем указатель мыши по ячейкам таблицы со значениями до

конца таблицы по . Отпускаем левую кнопку мыши. Появляется ряд рассчитанных машиной числовых значений . При = 100 = 21739,5. При = 54, как и ожидалось, знаменатель функции обращается в нуль, и ЭВМ указывает пользователю на запрещенную операцию деления на нуль. При этом машина по умолчанию выставляет вместо бесконечно большой положительной или отрицательной величины число «1034» или «-1034», к которым и будут стремиться графические зависимости при разрыве второго рода исследуемой функции вблизи точки = 54.
Выделяем все ячейки полученной таблицы аналогично пункту 6. Машина готова к построению графической зависимости от .
Вызываем «Мастера диаграмм»: нажимаем соответствующую кнопку на верхней горизонтальной панели управления экрана процессора Excel. При нажатии кнопок «График» и затем «Предварительный просмотр» в появившемся окне диаграмм появляется качественный вид рассчитанной графической зависимости, причем в этом виде значения функции по оси ординат могут быть не связаны с выставленными ЭВМ по умолчанию со значениями аргумента функции. Для того, чтобы привести в соответствие числовые значения по осям графика, надо нажать кнопку «Далее», открыть вкладку «Ряд», поставить курсор в поле «Подписи по оси », затем указателем мыши дополнительно выделить ячейки в строка . При нажатии кнопки «Готово» появляется точный график функции. Перетянуть график по полю «Листа» можно, наведя указатель мыши на поле графика, нажав и удерживая нажатой левую кнопку мыши (см. рис.).
Выделяем все ячейки полученной таблицы аналогично пункту 6. Машина готова к построению графической зависимости от .
Вызываем «Мастера диаграмм»: нажимаем соответствующую кнопку на верхней горизонтальной панели управления экрана процессора Excel. При нажатии кнопок «График» и затем «Предварительный просмотр» в появившемся окне диаграмм появляется качественный вид рассчитанной графической зависимости, причем в этом виде значения функции по оси ординат могут быть не связаны с выставленными ЭВМ по умолчанию со значениями аргумента функции. Для того, чтобы привести в соответствие числовые значения по осям графика, надо нажать кнопку «Далее», открыть вкладку «Ряд», поставить курсор в поле «Подписи по оси », затем указателем мыши дополнительно выделить ячейки в строка . При нажатии кнопки «Готово» появляется точный график функции. Перетянуть график по полю «Листа» можно, наведя указатель мыши на поле графика, нажав и удерживая нажатой левую кнопку мыши (см. рис.).
Слайд 5Рис. 2.2. Элементы предварительного решения задачи в Excel
Рис. 2.2. Элементы предварительного решения задачи в Excel
Слайд 6Рис.2.3. Вдвое увеличено поле исследования функции. Задача решена
Рис.2.3. Вдвое увеличено поле исследования функции. Задача решена
Слайд 7 Если вид графика не позволяет определенно судить о характере изменения функции
Если вид графика не позволяет определенно судить о характере изменения функции

во всём диапазоне изменения аргумента, следует изменить один или оба предела изменения аргумента, сохраняя или одновременно меняя шаг по . Для этого достаточно первые два числовых значения изменить на «-200» и «-198». После этого можно протянуть эту строку таблицы до числа «200». Машина сама изменит числовые значения функции в нижележащей строке. Затем снова надо выделить область «Листа» с новой таблицей и так же использовать «Мастера диаграмм». На рис. 2 пределы расширились от «–200» до «200» при том же шаге, т.е. строка таблицы заняла 200 ячеек. Поскольку наибольшее число ячеек в горизонтальной строке таблицы равно 256 (числу столбцов), то наименьший избранный пользователем в данном случае шаг не должен быть более (200 + 200)/(256 – 1 – 1) = 1,574803149 (размерность переменной на одну ячейку). Здесь одна ячейка отдана на обозначение переменной, другая – на обозначение начального предела. Величина «400» - величина диапазона изменения этой переменной.
Если вид графика качественно отличается от прогнозируемого, следует соответственно изменить шаг по . Для этого во второй ячейке по поставим число «-160». На рис. 3 существенно, до величины «40», увеличен шаг, поэтому построение графика функции более грубое, информация о её характеристиках при вблизи значения «54» потеряна. Ценности работа с таким качеством выполнения технологии компьютерного проектирования практически не представляет.
Если вид графика качественно отличается от прогнозируемого, следует соответственно изменить шаг по . Для этого во второй ячейке по поставим число «-160». На рис. 3 существенно, до величины «40», увеличен шаг, поэтому построение графика функции более грубое, информация о её характеристиках при вблизи значения «54» потеряна. Ценности работа с таким качеством выполнения технологии компьютерного проектирования практически не представляет.
 Отчет о ведении сообществ в социальных медиа
Отчет о ведении сообществ в социальных медиа Что такое 3D-графика и как она устроена
Что такое 3D-графика и как она устроена kumir 1
kumir 1 Регистрация и запись ребенка в электронном каталоге программ дополнительного образования Навигатор
Регистрация и запись ребенка в электронном каталоге программ дополнительного образования Навигатор Операции над графами
Операции над графами Вспомогательные режимы работы
Вспомогательные режимы работы Prezentatsia_Excel
Prezentatsia_Excel 6-12-1-grafiki-i-diagrammy
6-12-1-grafiki-i-diagrammy Программы-переводчики
Программы-переводчики Разрешения на доступ к этой презентации
Разрешения на доступ к этой презентации Educator Onlain. Воспитатель и его работа в период пандемии COVID-19
Educator Onlain. Воспитатель и его работа в период пандемии COVID-19 Latest Wireless Sensor Network thesis help and research guidance
Latest Wireless Sensor Network thesis help and research guidance УРВ решение для SMB ZKTime.net. Подключение Telegram к ZKTime.Net
УРВ решение для SMB ZKTime.net. Подключение Telegram к ZKTime.Net Сжатие данных
Сжатие данных Практическая работа. Электронная почта
Практическая работа. Электронная почта Бой коробля и субмарины
Бой коробля и субмарины Система автоматического управления газоперекачивающим агрегатом МСКУ 5000-01
Система автоматического управления газоперекачивающим агрегатом МСКУ 5000-01 Работа в Excel 2007. Основы
Работа в Excel 2007. Основы Визуализация данных
Визуализация данных Аппаратная реализация компьютера и периферийные устройства
Аппаратная реализация компьютера и периферийные устройства NASA смоделировало вид Луны на весь 2021 год
NASA смоделировало вид Луны на весь 2021 год Торговые элементы. Штрих-коды. Этикетки
Торговые элементы. Штрих-коды. Этикетки Открой для себя новые возможности в команде Первых. Просто и коротко о команде Первого БИТа
Открой для себя новые возможности в команде Первых. Просто и коротко о команде Первого БИТа Aplikací pro cestování a dopravu
Aplikací pro cestování a dopravu Информация. Свойства и единицы измерения
Информация. Свойства и единицы измерения Интеллектуальный анализ данных (Data Mining)
Интеллектуальный анализ данных (Data Mining) Памятка для студентов заочной формы обучения по работе с электронными ресурсами через личный кабинет
Памятка для студентов заочной формы обучения по работе с электронными ресурсами через личный кабинет Разработка баз данных
Разработка баз данных