Представление графов. Топологическая сортировка

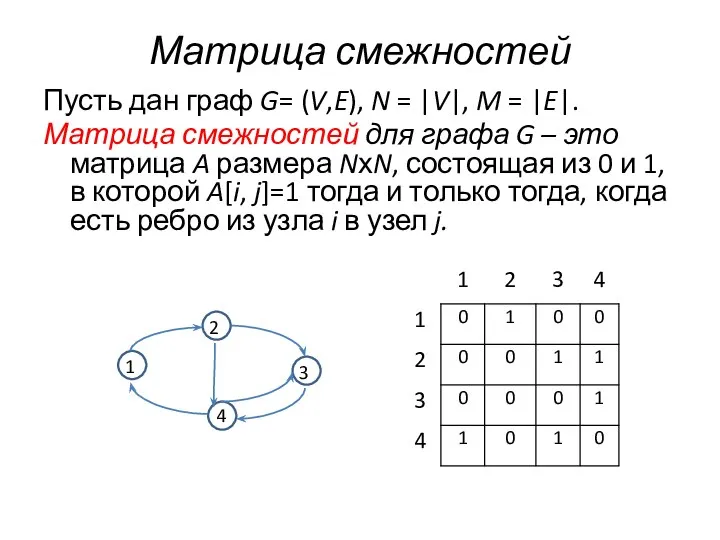
Матрица смежностей
Пусть дан граф G= (V,E), N = |V|, M = |E|.
Матрица смежностей для графа G – это матрица A размера NхN, состоящая из 0 и 1, в которой A[i, j]=1 тогда и только тогда, когда есть ребро из узла i в узел j.
1
3
2
4

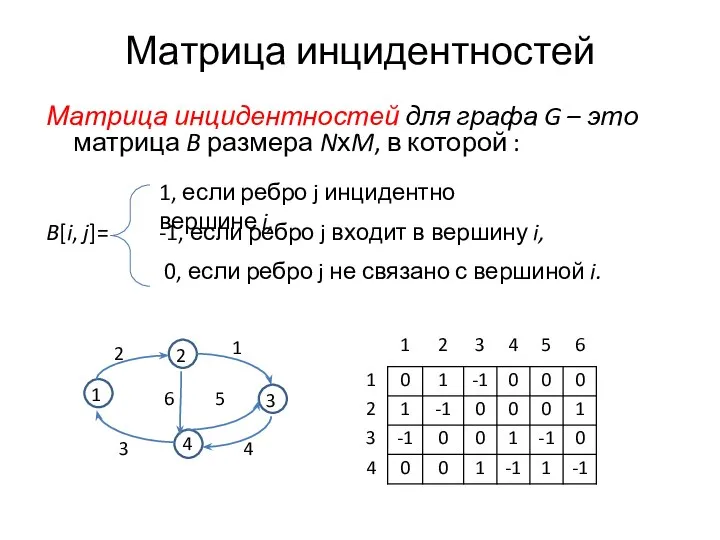
Матрица инцидентностей
Матрица инцидентностей для графа G – это матрица B размера NхM, в которой :
B[i, j]=
1, если ребро j инцидентно вершине i,
-1, если ребро j входит в вершину i,
0, если ребро j не связано с вершиной i.
1
3
2
4
6
5
4
3
2
1

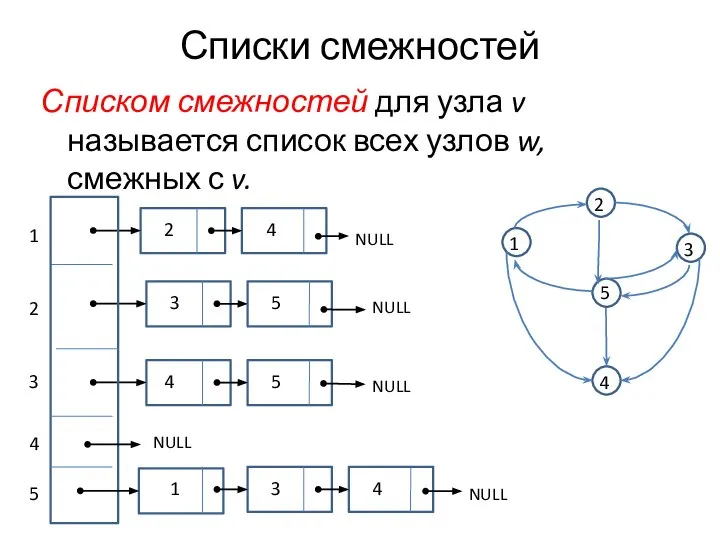
Списки смежностей
Списком смежностей для узла v называется список всех узлов w, смежных с v.
1
3
2
5
4
NULL
1
4
3
1
5
4
5
3
4
2
5
4
3
2
NULL
NULL
NULL
NULL

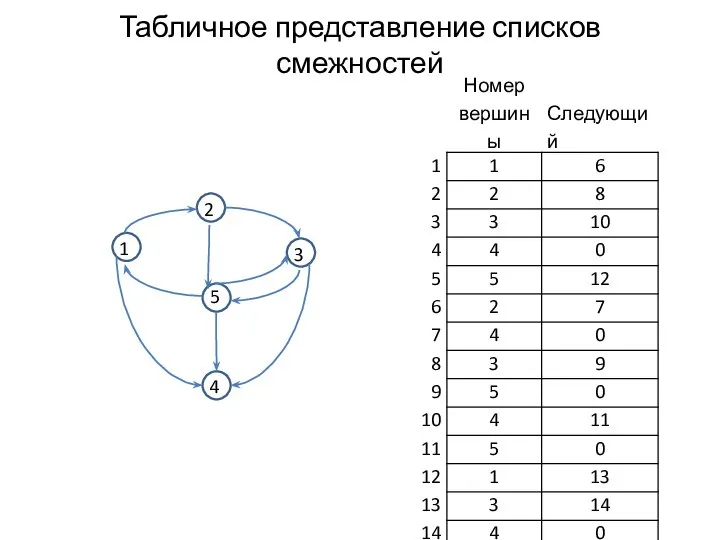
Табличное представление списков смежностей
1
3
2
5
4

Топологическая сортировка
Определение. Частичным порядком на множестве А называется отношение R, определенное на А и такое, что
R транзитивно,
для всех a ∈ A утверждение aRa ложно, т.е. отношение R иррефлексивно.
Из свойств (1) и (2) следует, что если aRb истинно, то bRa ложно (асимметричность).

Примеры частичного порядка:
решение большой задачи разбивается на ряд подзадач, над которыми установлен частичный порядок: без решения одной задачи нельзя решить несколько других;
последовательность чтения курсов в учебных программах: один курс основывается на другом;
выполнение работ: одну работу следует выполнить раньше другой.

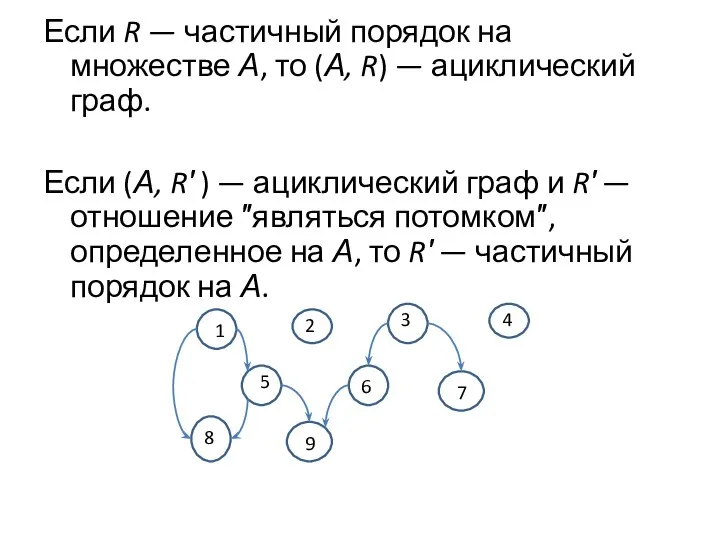
Если R — частичный порядок на множестве А, то (А, R) — ациклический граф.
Если (А, R′ ) — ациклический граф и R′ — отношение ″являться потомком″, определенное на А, то R′ — частичный порядок на А.
1
2
3
4
5
6
7
8
9

Определение. Линейный порядок R на множестве А — это такой частичный порядок, что если a и b принадлежат А, то либо aRb, либо bRa, либо a = b.
Если А — конечное множество, то линейный порядок R удобно представлять , считая все элементы множества А расположенными в виде последовательности
a1, a2,..., an,
для которой имеет место aiRaj тогда и только тогда, когда i < j.

Если задан частичный порядок R на множестве А, часто бывает нужен линейный порядок, содержащий этот частичный порядок.
Эта проблема вложения частичного порядка в линейный называется топологической сортировкой.
Формально можно сказать, что
частичный порядок R на множестве А
вложен в линейный порядок R',
если R‘ — линейный порядок и R⊆R',
т. е. aRb влечет aR'b для всех а и b из А.

1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
Топологическая сортировка. Пример

Алгоритм. Топологическая сортировка
Вход. Частичный порядок R на конечном множестве А.
Выход. Линейный порядок R' на А, для которого R ⊆ R'.
Метод. Так как А — конечное множество, линейный порядок R' на А можно представить в виде списка a1, a2, ..., аn, для которого
ai R' aj, если i < j, и А = {а1, a2, ..., аn}.
Эта последовательность элементов строится с помощью следующих шагов:
Положить i=1, Аi=А и Ri=R.
Если Ai пусто, остановиться и выдать a1, ..., аi, в качестве искомого линейного порядка. В противном случае выбрать в Аi такой элемент аi+1 что a' R аi+1, ложно для всех a' ∈ Ai.
Положить Ai+1= Ai \ {аi+1} и Ri+1= Ri \ ({ai+1}×Ai+1). Затем увеличить i на единицу и повторить шаг 2.

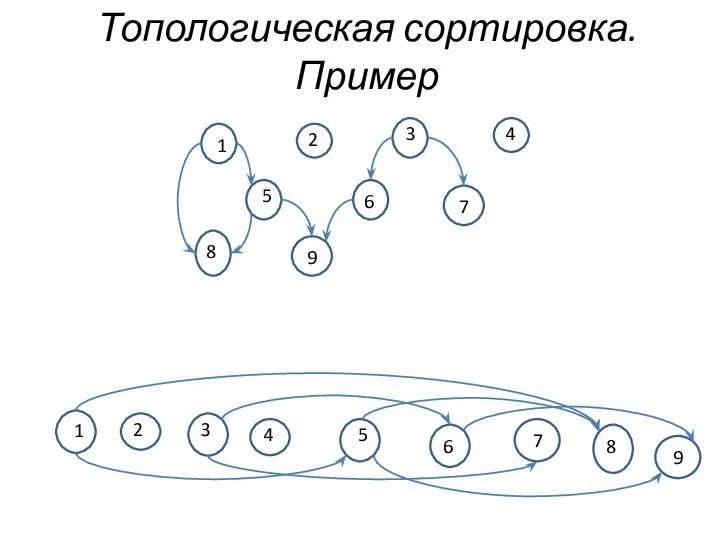
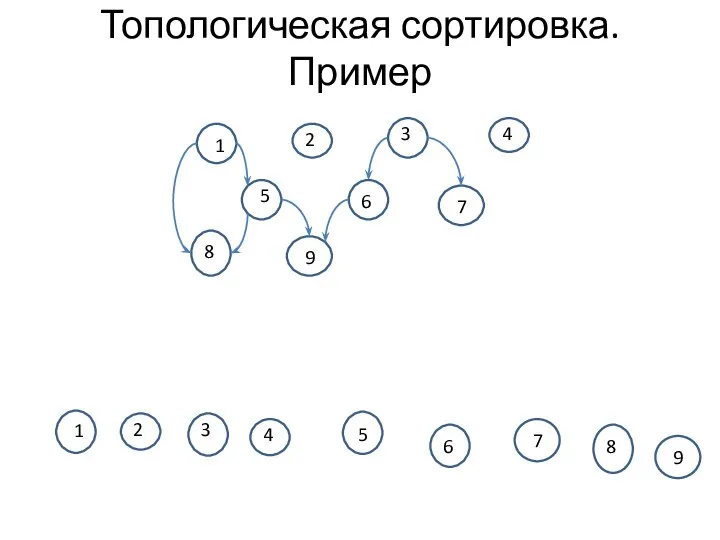
Топологическая сортировка. Пример
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9

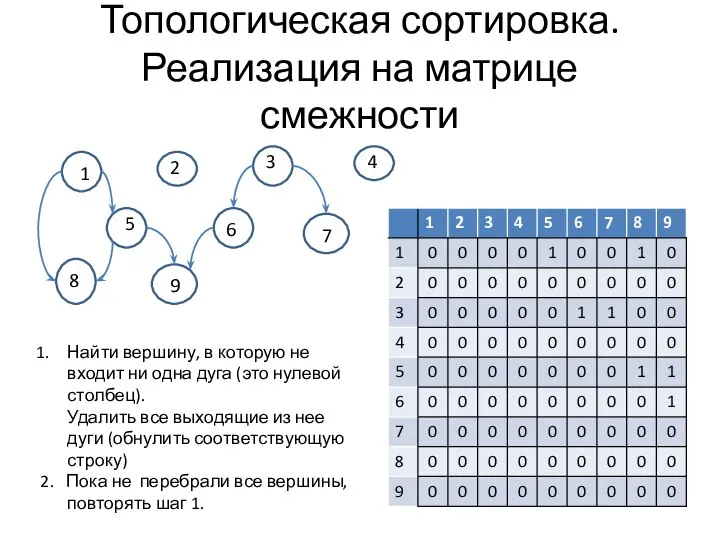
Топологическая сортировка. Реализация на матрице смежности
1
2
3
4
5
6
7
8
9
Найти вершину, в которую не входит ни одна дуга (это нулевой столбец).
Удалить все выходящие из нее дуги (обнулить соответствующую строку)
2. Пока не перебрали все вершины, повторять шаг 1.

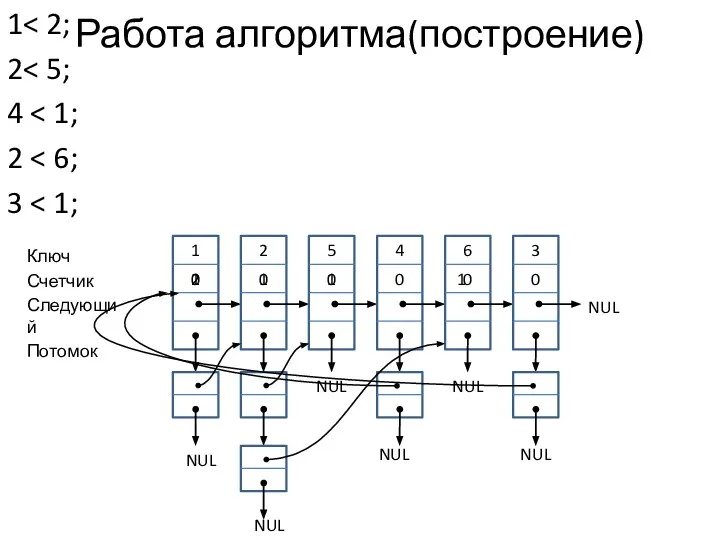
Топологическая сортировка.
Реализация на иерархических списках
2
1
Ключ – номер вершины
Счетчик – количество входящих дуг
Следующий – указатель на следующую вершину
Потомок – список указателей на потомков
NUL
Элемент списка вершин графа:

Работа алгоритма(построение)
1
2
2
1
5
1
4
0
6
1
3
0
Ключ
Счетчик
Следующий
Потомок
1
0
0
0
0
NUL
1< 2;
2< 5;
4 < 1;
2 < 6;
3 < 1;
NUL
NUL
NUL
NUL
NUL
NUL