Работа с двумерными массивами

Диагонали, параллельные главной
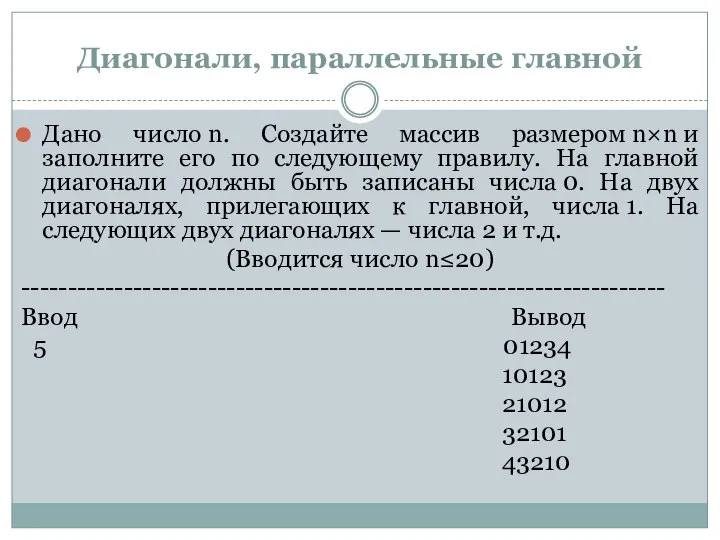
Дано число n. Создайте массив размером n×n и заполните его по следующему правилу. На главной диагонали должны быть записаны числа 0. На двух диагоналях, прилегающих к главной, числа 1. На следующих двух диагоналях — числа 2 и т.д.
(Вводится число n≤20)
---------------------------------------------------------------------
Ввод Вывод
5 01234
10123
21012
32101
43210

Решение
n=int(input())
a=[[str(abs(i-j)) for j in range(n)] for i in range(n)]
for row in a: print(' '.join(row))

Заполнение змейкой
По данным числам n и m заполните двумерный массив размером n×m числами от 1 до n×m “змейкой”, как показано в примере.
(Вводятся два числа n≤40n≤40 и m≤40m≤40)
----------------------------------------------------------------
Ввод Вывод
3 5 1 2 3 4 5
10 9 8 7 6
11 12 13 14 15

Решение
n, m=map(int, input().split())
a=[[str (1+j+i*m) for j in range(m)] for i in range (n)]
for i in range (1,n,2):
a[i]=a[i][::-1]
for row in a:
print(' '.join(row))

Шахматная доска
Даны два числа n и m. Создайте двумерный массив размером n×m и заполните его символами 1 и 0 в шахматном порядке. В левом верхнем углу должна стоять единица.
----------------------------------------------------------------
Ввод Вывод
3 4 1 0 1 0
0 1 0 1
1 0 1 0

Решение
n, m=map(int, input().split())
A = [['10'[(j + i) % 2] for j in range(m)] for i in range(n)]
for i in range (n):
for j in range (m):
print(A[i][j], end=‘ ‘)
print()

Слева направо, сверху вниз
Даны два числа n и m. Создайте двумерный массив размером n×m и заполните его в соответствии с примером.
----------------------------------------------------------------
Ввод Вывод
4 4 0 1 2 3
4 5 6 7
8 9 10 11
12 13 14 15

Решение
n, m=map(int, input().split())
A=[[i+j*m for i in range(m)] for j in range (n)]
for i in range (n):
for j in range (m):
print(A[i][j], end=‘ ‘)
print()

Сверху вниз, слева направо
Даны два числа n и m. Создайте двумерный массив размером n×m и заполните его в соответствии с примером.
----------------------------------------------------------------
Ввод Вывод
5 6 0 5 10 15 20 25
1 6 11 16 21 26
2 7 12 17 22 27
3 8 13 18 23 28
4 9 14 19 24 29

Решение
n, m=map(int, input().split())
A=[[i*n+j for i in range(m)] for j in range(n)]
for i in range (n):
for j in range (m):
print(A[i][j], end=‘ ‘)
print()

Квадранты
Дано число n. Создайте массив размером n×n и заполните его по следующему правилу. На главной и побочных диагоналях стоят нули, эти диагонали делят массив на четыре части. В верхней части записаны единицы, в правой записаны двойки, в нижней записаны тройки, в левой записаны четверки.
--------------------------------------------------------------------------------------
Ввод Вывод
8 0 1 1 1 1 1 1 0
4 0 1 1 1 1 0 2
4 4 0 1 1 0 2 2
4 4 4 0 0 2 2 2
4 4 4 0 0 2 2 2
4 4 0 3 3 0 2 2
4 0 3 3 3 3 0 2
0 3 3 3 3 3 3 0

Решение
n= int(input())
A = [[0 if i == j or i == n - j - 1 else
1 if i < j < n - i - 1 else
2 if i < j else
3 if j > n - i - 1 else 4 for j in range(n)] for i in range(n)]
for i in range (n):
for j in range (n):
print(A[i][j], end=‘ ‘)
print()

Количество маршрутов в прямоугольной таблице
В прямоугольной таблице N×MN×M вначале игрок находится в левой верхней клетке. За один ход ему разрешается перемещаться в соседнюю клетку либо вправо, либо вниз (влево и вверх перемещаться запрещено). Посчитайте, сколько есть способов у игрока попасть в правую нижнюю клетку.
(Вводятся два числа N и M — размеры таблицы 1≤N≤10,1≤M≤10)
------------------------------------------------------------------
Ввод Вывод
1 10 1

Решение
from math import factorial
M, N = map(int,input().split())
M -= 1
N -= 1
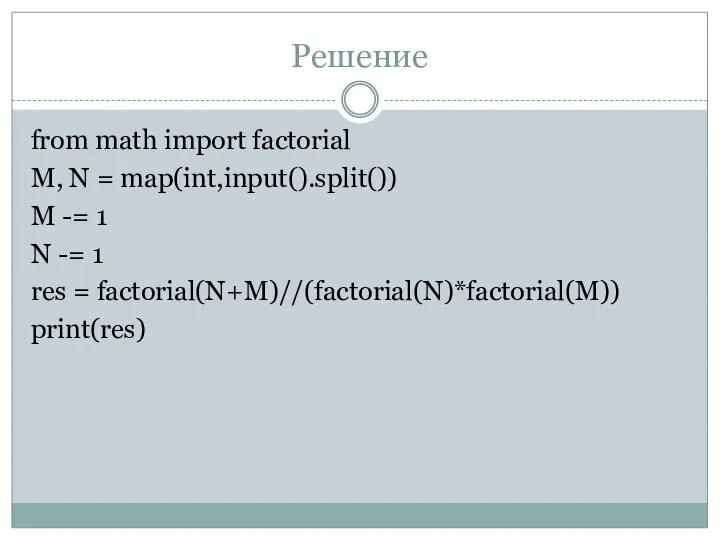
res = factorial(N+M)//(factorial(N)*factorial(M))
print(res)

Cамый дешёвый путь
В каждой клетке прямоугольной таблицы N×M записано некоторое число. Изначально игрок находится в левой верхней клетке. За один ход ему разрешается перемещаться в соседнюю клетку либо вправо, либо вниз (влево и вверх перемещаться запрещено). При проходе через клетку с игрока берут столько килограммов еды, какое число записано в этой клетке (еду берут также за первую и последнюю клетки его пути).
Требуется найти минимальный вес еды в килограммах, отдав которую игрок может попасть в правый нижний угол.

Входные данные и пример
Вводятся два числа N и M — размеры таблицы 1≤N≤20,1≤M≤20. Затем идёт N строк по M чисел в каждой — размеры штрафов в килограммах за прохождение через соответствующие клетки (числа от 0 до 100).
------------------------------------------------------------------------
Ввод Вывод
5 5 11
1 1 1 1 1
3 9 9 9 9
1 1 1 1 1
2 2 2 2
1 1 1 1 1 1

Решение
n, m=map(int, input().split())
p=[list(map(int, input().split())) for i in range (n)]
a=[[0]*m for i in range (n)]
a[0][0]=p[0][0]
for j in range (1,m):
a[0][j]=a[0][j-1]+p[0][j]
for i in range (1,n):
a[i][0]=a[i-1][0]+p[i][0]
for i in range (1,n):
for j in range (1,m):
a[i][j]=min(a[i][j-1],a[i-1][j])+p[i][j]
print(a[-1][-1])

Шашку — в дамки
На шахматной доске (8×8) стоит одна белая шашка. Сколькими способами она может пройти в дамки?
(Белая шашка ходит по диагонали. на одну клетку вверх-вправо или вверх-влево. Шашка проходит в дамки, если попадает на верхнюю горизонталь)
(Вводятся два числа от 1 до 8: номер столбца (считая слева) и строки (считая снизу), где изначально стоит шашка)
------------------------------------------------------------------
Ввод Вывод
3 7 2

Решение
n, m=map(int, input().split())
f=[[0]*10 for i in range(9)]
f[m][n]=1
for i in range (m+1,9):
for j in range (1,9):
f[i][j]=f[i-1][j-1]+f[i-1][j+1]
print(sum(f[8]))

Вывести маршрут максимальной стоимости
В левом верхнем углу прямоугольной таблицы размером N×M находится черепашка. В каждой клетке таблицы записано некоторое число. Черепашка может перемещаться вправо или вниз, при этом маршрут черепашки заканчивается в правом нижнем углу таблицы.
Подсчитаем сумму чисел, записанных в клетках, через которую проползла черепашка (включая начальную и конечную клетку). Найдите наибольшее возможное значение этой суммы и маршрут, на котором достигается эта сумма.

Входные и выходные данные
Входные данные
В первой строке входных данных записаны два натуральных числа N и M, не превосходящих 100 — размеры таблицы. Далее идут N строк, каждая из которых содержит M чисел, разделенных пробелами — описание таблицы. Все числа в клетках таблицы целые и могут принимать значения от 0 до 100.
Выходные данные
Первая строка выходных данных содержит максимальную возможную сумму, вторая — маршрут, на котором достигается эта сумма. Маршрут выводится в виде последовательности, которая должна содержать N−1 букву D, означающую передвижение вниз и M−1 букву R, означающую передвижение направо. Если таких последовательностей несколько, необходимо вывести ровно одну (любую) из них.

Пример
Ввод Вывод
5 5 74
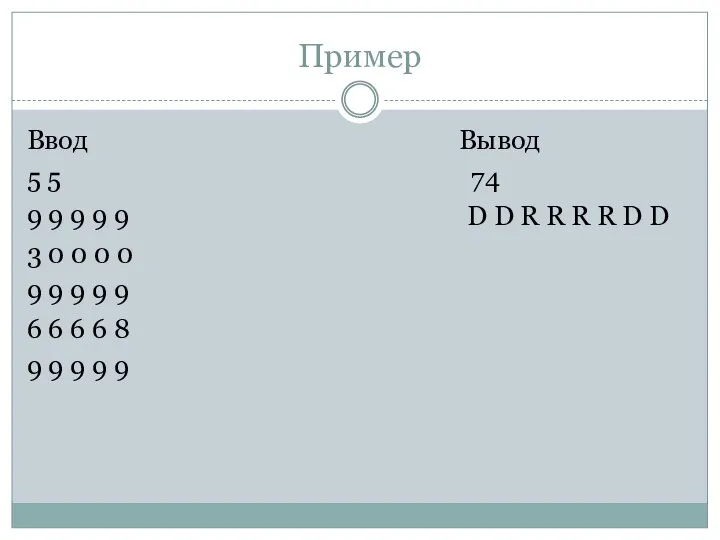
9 9 9 9 9 D D R R R R D D
3 0 0 0 0
9 9 9 9 9
6 6 6 6 8
9 9 9 9 9