Слайд 2Типом данных называется определение некоторой структуры данных, формы ее представления в памяти

и набора возможных операций с ней
Понятие типа включает в себя следующую информацию об элементе данных:
допустимый набор значений, которые объект этого типа может принимать в процессе работы программы (совокупность всех указанных значений мы будем называть областью определения типа)
состав операций, которые разрешено выполнять над объектами данного типа
способ представления элемента данных рассматриваемого типа в памяти машины
правила выполнения всякой операции из допустимого для этого типа набора операций
Слайд 3Данные, обрабатываемые средствами языка Си, могут иметь различную структуру, формы представления в

компьютере
Имеются типы данных, для которых формы представления и операции над ними реализованы в самом процессоре. Такие типы данных в Си называются базовыми
К базовым типам относятся типы char, int, float, double
Переменные определенные как char, int, float, double имеют различную структуру в памяти
Слайд 4Все данные записываются в компьютере в виде некоторой последовательности битов (0 или

1)
В большинстве компьютеров нельзя обратиться к конкретному биту. Можно записывать или читать только байт или машинное слово
Машинное слово - двоичное число определенной размерности, используемое в основной системе команд компьютера для обработки данных. Размерность слова зависит от вида компьютера
Для того чтобы определить сколько бит занимает переменная определенного типа необходимо использовать оператор sizeof(e)
Слайд 5 sizeof(e) - число байт, требуемых для размещения данных типа е.

или
sizeof(тип) - число байт, требуемых для размещения объектов типа
Пример:
int a, a1;
int b=1;
a=sizeof(a);
a1=sizeof(int);
В результате a и a1 будут иметь одно и тоже значение.
Слайд 6Подобным образом можно определить размер, которые занимают переменные различных типов.
В Visual Studio

.NET базовые типы унифицированы и не зависят от типа компьютера.
В нашем случае и a и a1 будут равны 2. (Два байта или 32 бита для переменных типа int)
Слайд 7Переменной в языке Си называется область памяти для хранения данных, имеющая имя

и некоторую внутреннюю структуру (тип данных)
Любая переменная, которая используется в программе, должна быть определена (предварительно описана как char, int, float, double)
В процессе анализа определения переменной транслятором выполняются следующие действия:
вводится имя переменной, которое используется для обращения к ней в программе
задается тип данных (структура данных), к которому относится переменная
определяется начальное значение переменной (инициализация)
транслятором распределяется память в программе для размещения переменной
определяются характеристики переменной, которыми она будет обладать в программе (область действия, время жизни)
Слайд 8
С точки зрения языка Си, всякая переменная величина отождествляется с ее именем,

или идентификатором
С позиции же компьютера, она рассматривается как изменяющееся во времени содержимое некоторой области оперативной памяти
Слайд 91. Целые числа без знака
Числа без знака - это положительные числа

Для кодировки используется все разряды машинного слова
Ключевое слово unsigned используется как модификаторы основных типов данных
unsigned int b;
unsigned int a;
Слайд 10Байт (unsigned char)
Слово (unsigned int)
Двойное слово (unsigned long int)
Пример:
unsigned char a=77;
В оперативной

памяти выделяется область памяти размером 8 бит и в неё заносятся следующие значения:
7 6 5 4 3 2 1 0
0 1 0 0 1 1 0 1
Слайд 112. Целые со знаком
В системе команд любого компьютера имеется команда

сложения целых чисел без знака.
Операция вычитания, а также операция сложения чисел со знаком могут быть реализованы с использованием этой операции (сложения), но при условии специального кодирования отрицательных чисел, суть которого состоит в следующем:
старшая цифра числа представляет знак числа (0 - плюс, 1 - минус)
положительные числа представляются обычным образом
отрицательные числа представляются в дополнительном коде
Слайд 12Дополнительный код используется для представления целых отрицательных чисел. Это позволяет вместо операции

вычитания использовать обычное сложение, что упрощает конструкцию процессора
Слайд 13 Алгоритм перевода отрицательного числа в дополнительный код следующий:
каждая цифра отрицательного числа

заменяется на дополнение ее до n-1, где n - основание системы счисления, т.е. на цифру, которая в сумме с исходной дает n-1
к полученному числу добавляется 1
Такое представление чисел со знаком называется дополнительным кодом. При сложении чисел со знаком, представленных в дополнительном коде, результат получается также в дополнительном коде. При этом операция выполняется по правилам сложения целых без знака
Слайд 14 В двоичной системе счисления дополнение каждой цифры заменяется инвертированием двоичного разряда,

а с учетом представления знака старшим разрядом получается простой способ получения представления отрицательного числа:
взять абсолютное значение числа в двоичной системе
инвертировать все разряды, включая знаковый
добавить 1
Ту же самую последовательность операций нужно выполнить, чтобы получить из дополнительного кода абсолютное значение отрицательного числа.
Слайд 15Пример:
0 000 0000 0010 0101 - прямой код числа +35

1 111 1111 1101 1010 - инверсия всех бит (обратный код)
+
0 000 0000 0000 0001 - добавляем единицу мл.разряда
-----------------------------------------
1 111 1111 1101 1011 - дополнительный код числа (-35)
Слайд 163. Числа с плавающей точкой
Для использования чисел с дробной частью, а

также для расширения диапазона их представления вводится форма представления чисел с плавающей точкой
Как известно, любое число можно представить в виде
X=m*10 в степени p,
где 0.1 < m < 1 - значащая часть числа, приведенная к интервалу 0.1 - 1, a p - порядок числа
Аналогичная форма двоичного числа имеет вид
X=m*2 в степени p,
где 0.5 < m < 1 - мантисса, a p - двоичный порядок
Число с плавающей точкой можно представить в виде двух целых чисел со знаком (m и p), причем p - обычное целое со знаком, а m - представление дробной части, в которой десятичная точка считается расположенной после знакового разряда числа.
Слайд 17В Си имеется два типа данных для чисел с плавающей точкой:
обычной

(float)
двойной точности (double).
Слайд 18float
Переменной типа float компилятор отводит 4 байта памяти. Переменной выделяется 32-разрядное значение

одиночной точности в формате IEEE 754.
Eе численное значение хранится в нормализованном виде. Нормализация состоит в сдвиге значащих бит двоичного кода числа влево или вправо до тех пор, пока целая часть числа не станет равной единице. Разумеется, для сохранения численного значения каждая операция сдвига сопровождается соответствующим изменением двоичного порядка числа
Но если целая часть нормализованного двоичного числа всегда равна единице, ее можно вообще не хранить в ячейке памяти. Это экономит один "лишний" бит для записи мантиссы, увеличивая точность представления чисел. Конечно, при чтении числа из ячейки памяти такая "неявная единица", естественно, автоматически восстанавливается
Слайд 19
Скрытый разряд позволяет увеличить точность мантиссы с плавающей точкой с 23 разрядов,

непосредственно содержащихся в формате данных, до 24-х разрядов.
Это также означает, что мантисса любого нормализованного по формату IEEE числа больше или равна единице и меньше двух.
Слайд 20Порядок, полученный при нормализации, перед записью в ячейку памяти несколько видоизменяется. К

нему прибавляется фиксированное целое число так, чтобы он всегда был неотрицательным. Такой искусственно смещенный порядок называется характеристикой. Это избавляет от необходимости выделять специальный бит для хранения знака порядка и упрощает процедуру сравнения порядков чисел при выполнении над ними арифметических действий
Для чисел типа float прибавляется число 127, для чисел типа double прибавляется 1023.
Слайд 21
Структура ячейки памяти вещественной переменной типа float имеет вид (4 байта):
<-----¦----------------¦--------------------------------------->¦
¦1

бит¦ 8 бит ¦ 23 бита ¦
¦знак ¦ Характеристика ¦ Мантисса ¦
¦-----¦----------------¦----------------------------------------¦
Слайд 22В качестве примера рассмотрим запись в такую ячейку числа
15.375:
1111.011 -

двоичный код числа
Сдвигаем десятичную точку влево на три бита:
1.111011 * 2 в степени 3 - нормализованное число
Получим из порядка характеристику:
3 + 127 = 130 или 1000 0010 в двоичной записи
Учитывая, что число положительное, заполняем 4 байта памяти:
¦0¦100 0001 0¦111 0110 0000 0000 0000 0000¦
4 1 7 6 0 0 0 0
Слайд 23Стандарт IEEE также определяет несколько специальных типов данных для формата с плавающей

точкой однократной точности:
«НЕ ЧИСЛО» или NAN (Not-A-Number), тип данных с величиной характеристики 255 (все 1) и отличной от нуля дробной частью. Данные такого типа обычно используются как флаги для управления последовательностью исполнения команд, как инициализирующие значения переменных и как результаты некорректных операций, таких как 0 х ∞.
Бесконечность, тип данных с величиной порядка 255 и нулевой дробной частью. Обратите внимание, что дробная часть является знаковой величиной, поэтому в формате может быть представлена как положительная, так и отрицательная бесконечность.
Ноль, тип данных с нулевыми величинами порядка и дробной части. Подобно бесконечности, в формате могут быть представлены положительный и отрицательный нули.
Слайд 24double
Структура ячейки памяти вещественной переменной типа double имеет вид (8 байт):
<-------¦----------------¦--------------------------------------->¦

¦1 бит¦ 11 бит ¦ 52 бита ¦
¦--------¦----------------¦-----------------------------------------¦
1 бит – знак
11 бит – характеристика
52 бита мантисса
Для вычисления характеристики прибавляется 1023. Увеличены как диапазон, так и точность представления вещественных чисел
Слайд 25Переменные целых типов очень легко представить в виде 0 и 1.
Пример программы,

которая переводит безнаковое целое в двоичный вид. Реализаций таких программ с другим кодом может быть достаточно много.
void Binary(unsigned x)
{
int i; char a[32];
for (i = 0; i < 32; i++) { a[i] = x % 2; x = x / 2; }
printf("\n"); for (i = 31; i >= 0; i--) printf("%d", a[i]);
}
Слайд 26Перевести числа с плавающей запятой можно представив их в виде целых чисел.

Сделать это можно с помощью оператора объединения union
Объединение - это средство, позволяющее размещать данные различных типов в одном и том же месте оперативной памяти
С точки зрения грамматики языка Си, всякое объединение является переменной, принимающей в различное время выполнения программы значения различных типов
Память, выделяемая под объединения, определяется длиной наибольшего элемента в составе данного объединения. При этом все члены объединения хранятся в одной и той же области памяти с неизменным начальным адресом
Слайд 27В следующем примере одна и та же последовательность нулей и единиц интерпретируется

по разному в зависимости от типа вызова
union
{
unsigned k;
int k1;
float fk;
} a;
Обращение к различным частям union возможно как a.k, a.k1, a.fk.
Т.е. можно записать a.Fk =0.1; а прочитать безнаковую переменную a.k состоящую из того же набора нулей и единиц.
Слайд 28 Выделять отдельные структурные части чисел с плавающей запятой можно с помощью

операторов сдвига влево << или вправо >>.
Например выделить знак можно так.
unsigned Z(unsigned k)
{
k >>= 31;
return k;
}
Слайд 29 Выделить мантиссу можно так:
unsigned M(unsigned k) {
k <<= 9;
k >>= 9;
k

= k | 040000000;
return k;
}
Оператор k = k | 040000000; добавляет 1, которая не хранится в числе для экономии разрядов
Слайд 30Выделить характеристику можно так.
unsigned H(unsigned k)
{
k <<= 1;
k >>= 1;
k >>=

23;
return k;
}
Операторы
k <<= 1;
k >>= 1;
Нужны для того, чтобы устранить бит, который отвечает за знак
Слайд 31Последней частью проекта является перевод отдельных структурных частей float представленных в двоичном

виде в десятичный вид.
Для знака это просто. 0 = плюс, 1 – минус.
Для того, чтобы определить порядок через характеристику достаточно вычесть 127. Заметьте, что порядок может быть положительный или отрицательный.
p = b - 127;
b - характеристика
p – порядок
Имея мантиссу и порядок можно выделить целую и дробную часть с помощью операторов сдвига влево или вправо в зависимости от знака порядка. Операция сдвига влево может привести к выходу значения за разрядную сетку. Этот случай необходимо предусмотреть.
Слайд 32Определение целой части по мантиссе
unsigned cel(unsigned long long k, int p) //

p - порядок
{
unsigned long long a = 23 - p;
k >>= a;
return k;
}
Слайд 33Определение дробной части по мантиссе
unsigned drob(unsigned long long k, int p)
{
unsigned long

long b = k;
k <<= 41 + p; // 41=9+32.
k >>= 41 + p;
return k;
}
Слайд 34Теперь необходимо целую и дробную часть перевести в десятичный вид.
С целой частью

нет проблем. printf(" %d", b); (b – целая часть)
Для того, чтобы вывести дробную часть ее надо перевести в десятичный вид по правилам перевода дробных чисел.
Слайд 35Перевод дробной части производится следующим образом. Число умножается на показатель системы, в

которую мы хотим перевести до тех пор пока дробная часть не станет равна нулю.
Например перевод дробного числа в двоичный вид:
0.125 x 2 = 0.250 = 0 + 0.250
0.250 x 2 = 0.5 = 0 + 0.5
0.500 x 2 = 1.000 = 1 + 0.00
Результат составит последовательность целых частей
0.12510 = 0.0012
Слайд 36Перевод дробного числа 16-й вид:
0.2175 x 16 = 3.48 = 3

+ 0.48
0.48 x 16 = 7.68 = 7 + 0.68
0.68 x 16 = 10.88 = 10 (A) + 0.88
0.88 x 16 = 14.08 = 14 (E) + 0.08
0.08 x 16 = 1.28 = 1 + 0.28
0.28 x 16 = 4.48 = 4 + 0.48
0.217510 = 0.37AE1416



































 Повторение и закрепление изученного. Урок информатики в 4 классе
Повторение и закрепление изученного. Урок информатики в 4 классе Программирование в среде Robot C. Занятие 3
Программирование в среде Robot C. Занятие 3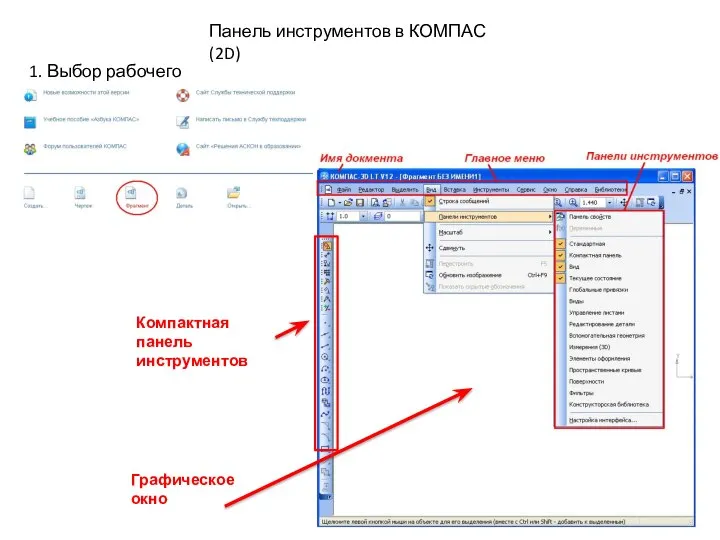 Панель инструментов в Компас-(2D). Практика 1
Панель инструментов в Компас-(2D). Практика 1 7-2-1
7-2-1 Текстовая информация. Единицы измерения
Текстовая информация. Единицы измерения Анимация. 3D графика
Анимация. 3D графика Персональные компьютеры и приложения
Персональные компьютеры и приложения Профессия моего папы инженер-программист
Профессия моего папы инженер-программист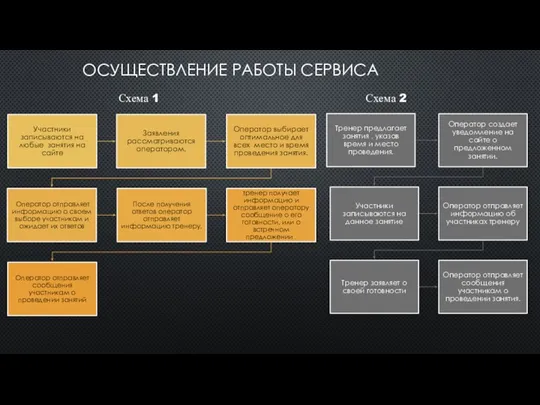 Осуществление работы сервиса
Осуществление работы сервиса Создание архива данных. Извлечение данных из архива
Создание архива данных. Извлечение данных из архива Табличные информационные модели. Моделирование и формализация
Табличные информационные модели. Моделирование и формализация Понятие информации
Понятие информации Программное обеспечение компьютера
Программное обеспечение компьютера Упаковка и распаковка данных с помощью программ-архиваторов. WinRAR
Упаковка и распаковка данных с помощью программ-архиваторов. WinRAR Настольные издательские системы
Настольные издательские системы 3D – печать. Механизмы и кинематика
3D – печать. Механизмы и кинематика Основы работы в Excel (урок 1)
Основы работы в Excel (урок 1) Спасибо, Дед Мороз!
Спасибо, Дед Мороз! Отношения между объектами
Отношения между объектами Информатика. Занятие 5
Информатика. Занятие 5 Принципы работы в соцсетях. Проектная деятельность
Принципы работы в соцсетях. Проектная деятельность Виды информации (интерактивный тест, 8 класс)
Виды информации (интерактивный тест, 8 класс) Порт PS/2
Порт PS/2 Information Technologies. Работа в области тестирования, разработки и продвижения интернет ресурсов
Information Technologies. Работа в области тестирования, разработки и продвижения интернет ресурсов Партнерская Система ЗОРАН как система искусственного интеллекта (часть первая: практическая значимость)
Партнерская Система ЗОРАН как система искусственного интеллекта (часть первая: практическая значимость) Отношение объектов и их множеств. Отношения между множествами. Отношение входитв состав
Отношение объектов и их множеств. Отношения между множествами. Отношение входитв состав Начало информационной эпохи. Постмодернизм
Начало информационной эпохи. Постмодернизм Открытый урок 29.09.2022 ОП.13 ССА 2.2 (1)
Открытый урок 29.09.2022 ОП.13 ССА 2.2 (1)