Разбор задач ЕГЭ. Оператор присваивания и ветвления. В3

Задача 1.
ИНФОРМАТИКА
2014г. Кирсанов Илья Андреевич ©
Дан фрагмент электронной таблицы:
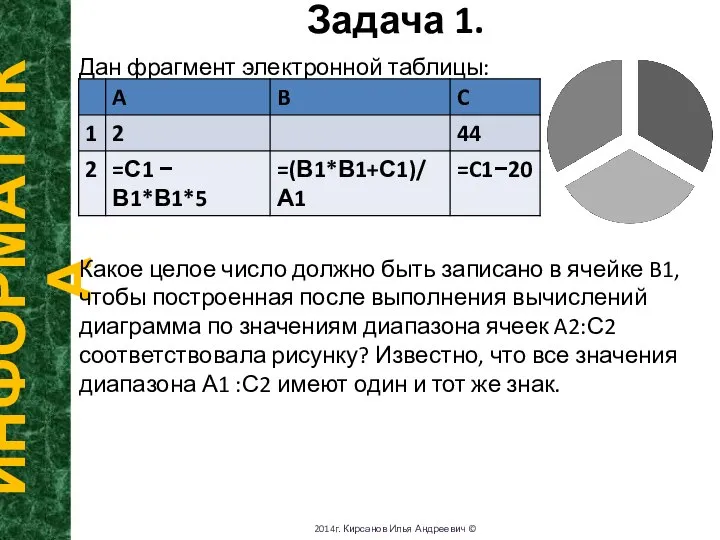
Какое целое число должно быть записано в ячейке B1, чтобы построенная после выполнения вычислений диаграмма по значениям диапазона ячеек A2:С2 соответствовала рисунку? Известно, что все значения диапазона А1 :С2 имеют один и тот же знак.

Задача 1.
ИНФОРМАТИКА
2014г. Кирсанов Илья Андреевич ©
Решение:
Преобразуем таблицу:
Из диаграммы следует, что значения в ячейках равны между собой. Следовательно, из того, что В1·В1/2 + 22 = 24, В1 = 2, либо В1 = −2. Все значения диапазона А1 :С2 имеют один и тот же знак, следовательно, ответ 2.
Ответ 2

Задача 2.
ИНФОРМАТИКА
2014г. Кирсанов Илья Андреевич ©
Дан фрагмент электронной таблицы:
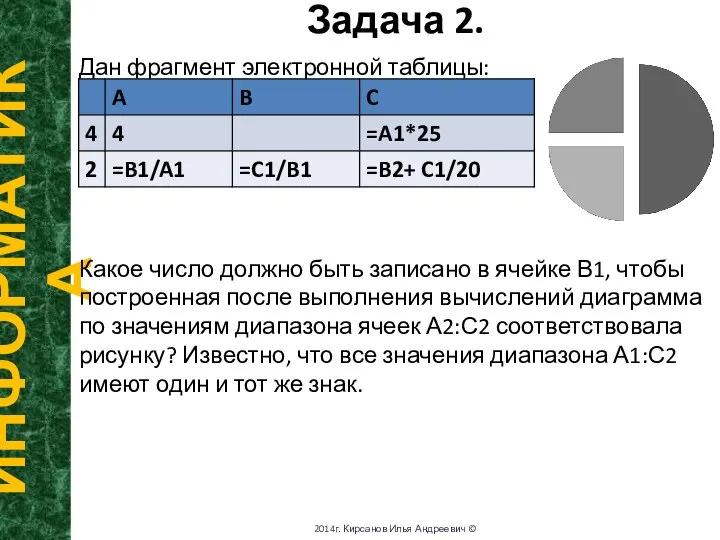
Какое число должно быть записано в ячейке В1, чтобы построенная после выполнения вычислений диаграмма по значениям диапазона ячеек А2:С2 соответствовала рисунку? Известно, что все значения диапазона А1:С2 имеют один и тот же знак.

Задача 2.
ИНФОРМАТИКА
2014г. Кирсанов Илья Андреевич ©
Решение:
Преобразуем таблицу:
Из диаграммы следует, что значения в 2-х ячейках равны между собой. Ячейки С2 и В2 не могут быть равны. Предположим, что равны ячейки А2 и В2, тогда В1=±20, А2=±5, В2=±5, С2=10 или 0, но этот результат не соответствует диаграмме, следовательно значение В1=20
Ответ 20

Задача 3.
ИНФОРМАТИКА
2014г. Кирсанов Илья Андреевич ©
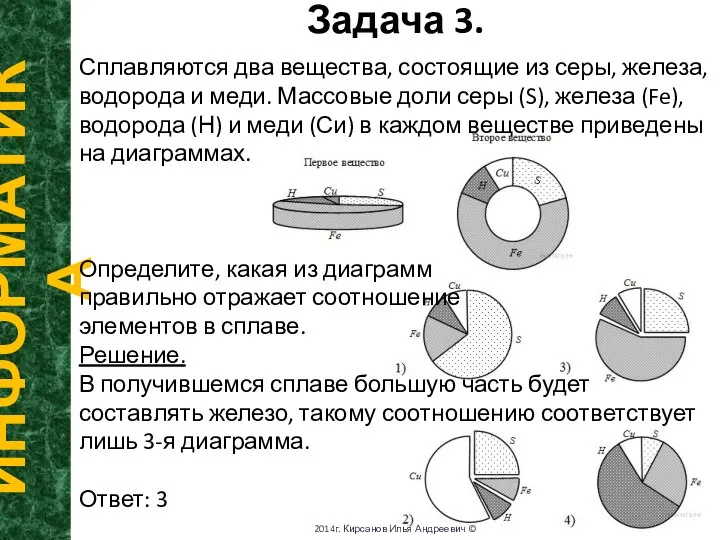
Сплавляются два вещества, состоящие из серы, железа, водорода и меди. Массовые доли серы (S), железа (Fe), водорода (Н) и меди (Си) в каждом веществе приведены на диаграммах.
Определите, какая из диаграмм
правильно отражает соотношение
элементов в сплаве.
Решение.
В получившемся сплаве большую часть будет составлять железо, такому соотношению соответствует лишь 3-я диаграмма.
Ответ: 3

Вопросы.
ИНФОРМАТИКА
2014г. Кирсанов Илья Андреевич ©
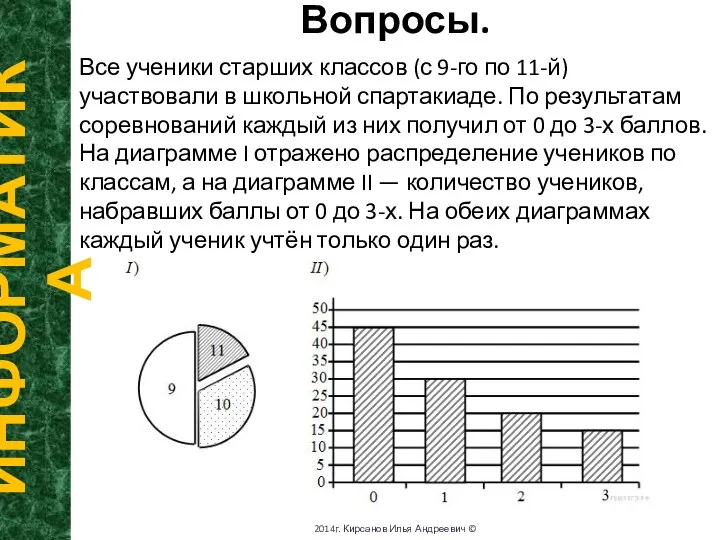
Все ученики старших классов (с 9-го по 11-й) участвовали в школьной спартакиаде. По результатам соревнований каждый из них получил от 0 до 3-х баллов. На диаграмме I отражено распределение учеников по классам, а на диаграмме II — количество учеников, набравших баллы от 0 до 3-х. На обеих диаграммах каждый ученик учтён только один раз.

Вопросы.
ИНФОРМАТИКА
2014г. Кирсанов Илья Андреевич ©
Имеются четыре утверждения:
1 ) Среди учеников 9-го класса есть хотя бы один, набравший 2 или 3 балла.
2 ) Все ученики, набравшие 0 баллов, могут быть 9-классниками.
3 ) Все 10-классники могли набрать ровно по 2 балла.
4 ) Среди набравших 3 балла нет ни одного 10-классника.
Какое из этих утверждений следует из анализа обеих диаграмм?
Ответ 2.