Слайд 2Алгоритм построения СЛС
1. Двоичное кодирование алфавитов X, Y, Q (возможно, появятся резервные

состояния).
2. Доопределение АТ на все состояния, в том числе и резервные. Цель: получить канонические уравнения наименьшей сложности.
3. Построение СЛС.
Слайд 4
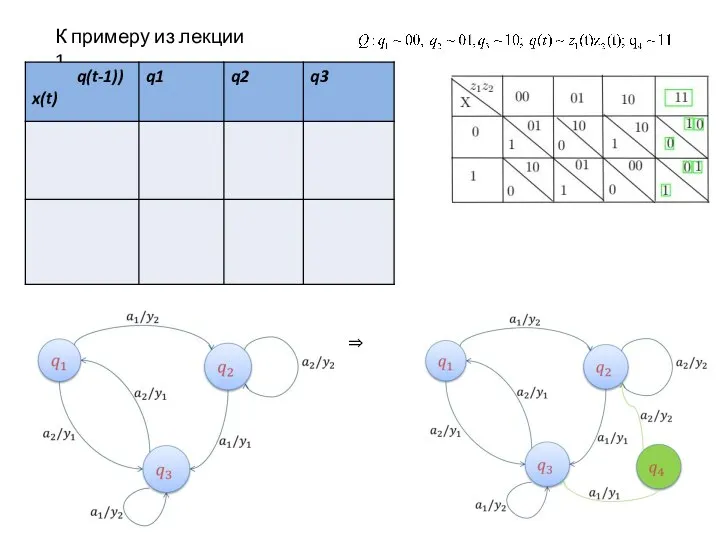
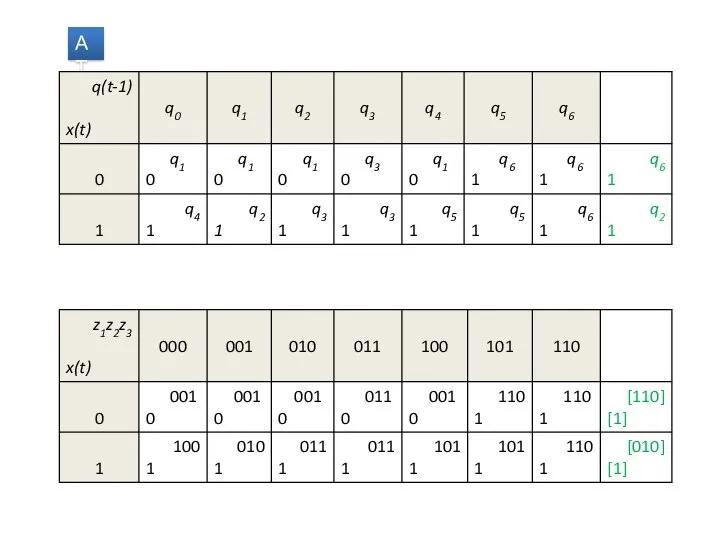
Решение: ДМ
0/0
0/0
1/1
1/1
1/1
0/1
1/1
0/0
1/1
1/1
0/1
1/1
0/0
q0
q1
q2
q3
q6
q5
q4
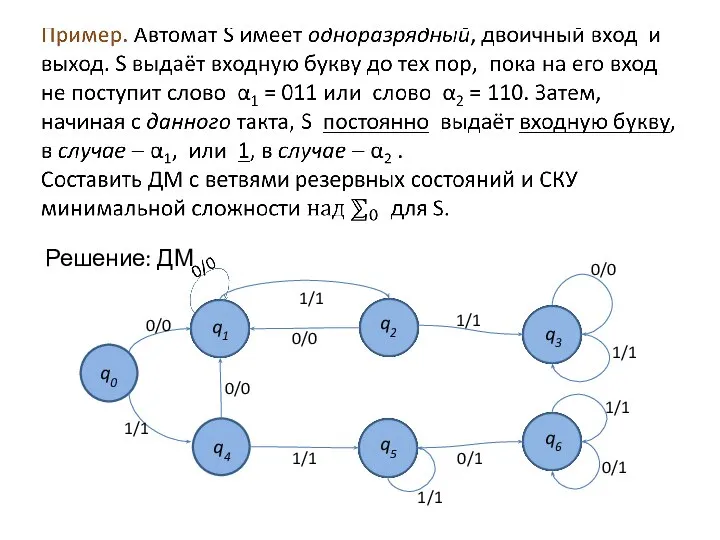
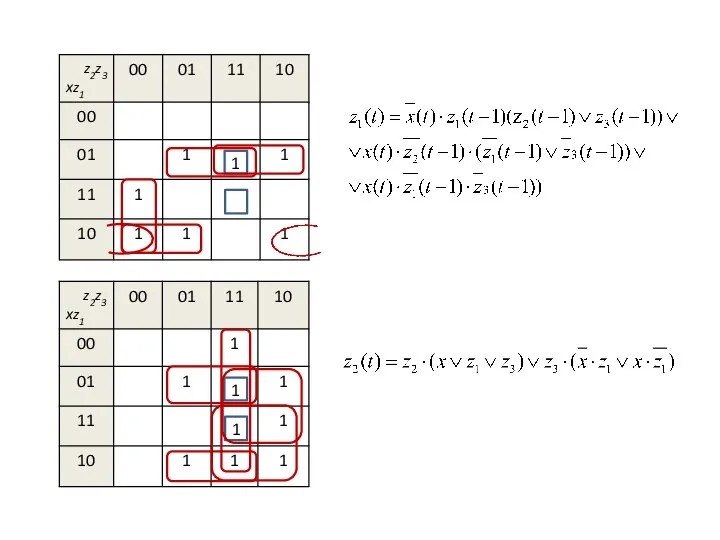
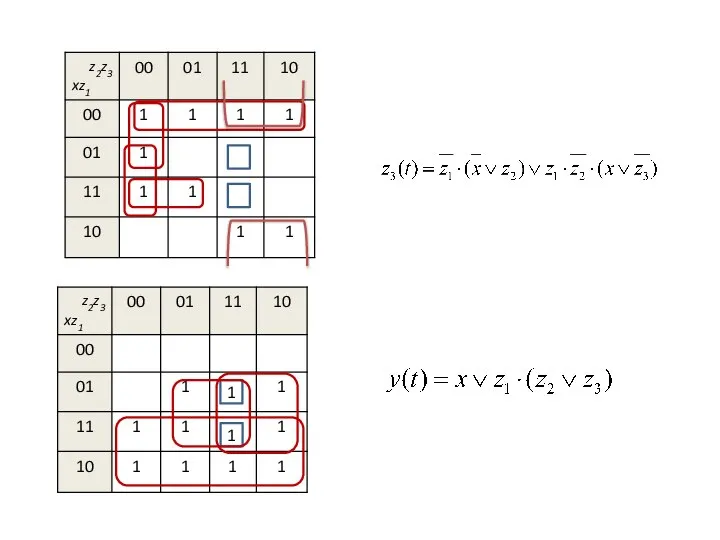
Слайд 8СЛС к примеру
Сложность схемы = 28
Слайд 90/0
0/0
1/1
1/1
1/1
0/1
1/1
0/0
1/1
1/1
0/1
1/1
0/0
q2
q3
q6
q5
q1
q4
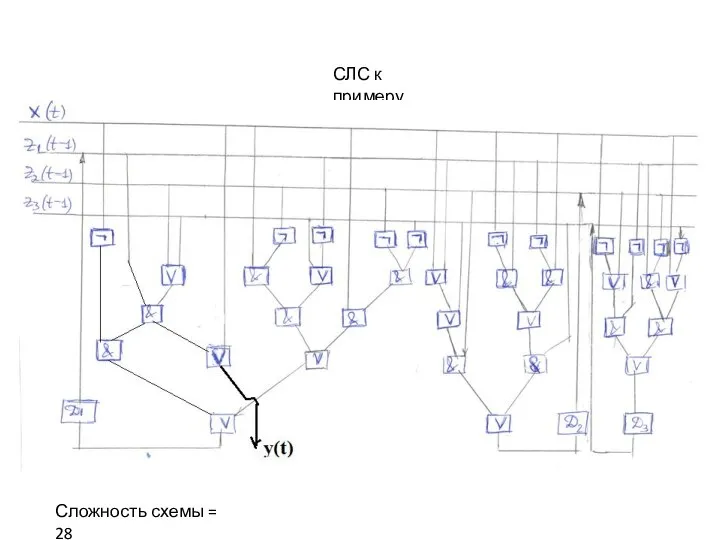
ДМ с ветвями резервных состояний
q0
q7
1/1
0/1
Слайд 10Доказательство теоремы о реализации произвольного автомата в виде СЛС

Слайд 12§3. Эквивалентные состояния и эквивалентные автоматы.

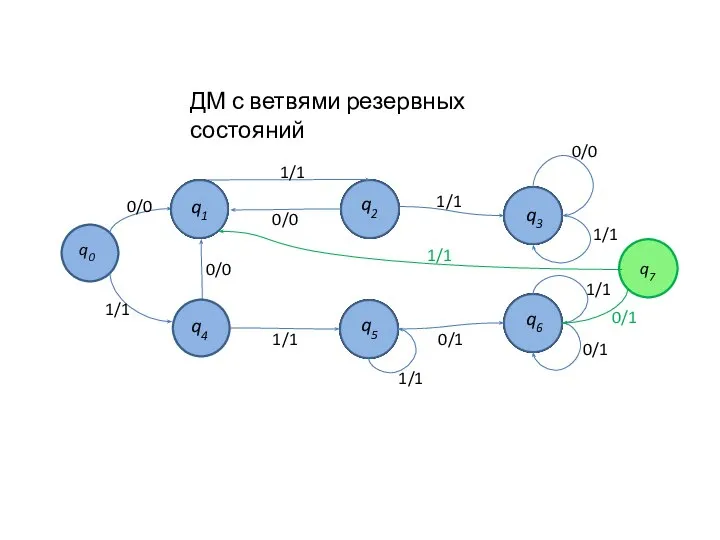
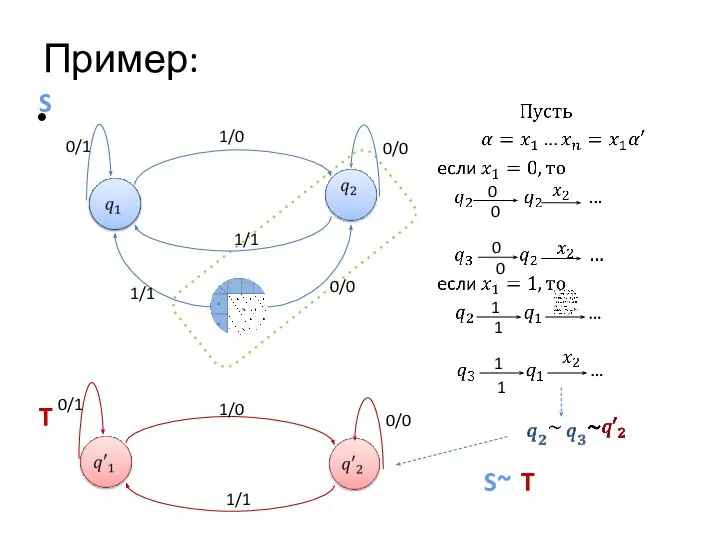
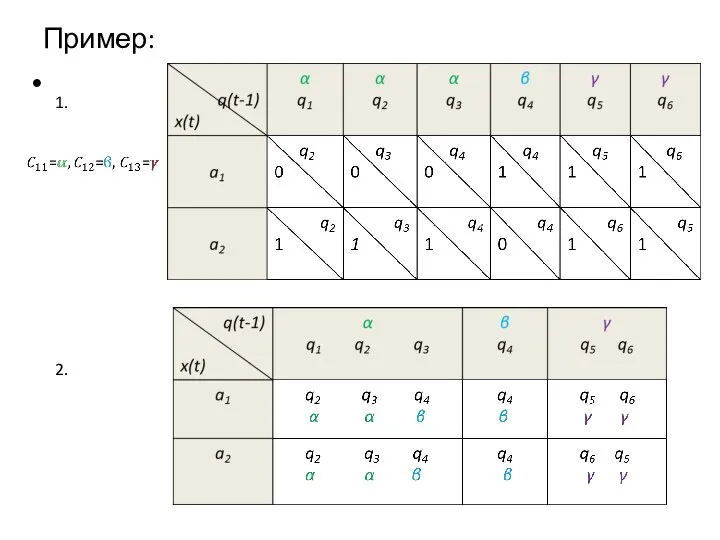
Слайд 13Пример:
1/0
0/0
0/0
1/1
1/1
0/1
0
0
0
0
1
1
1
1
S
T
1/0
1/1
S~
T
0/0
0/1
Слайд 15§4. Теорема о существовании минимального автомата
x
x

Слайд 19§5. Алгоритм минимизации автомата.
(алгоритм Ауфенкампа и Хона)

Слайд 25
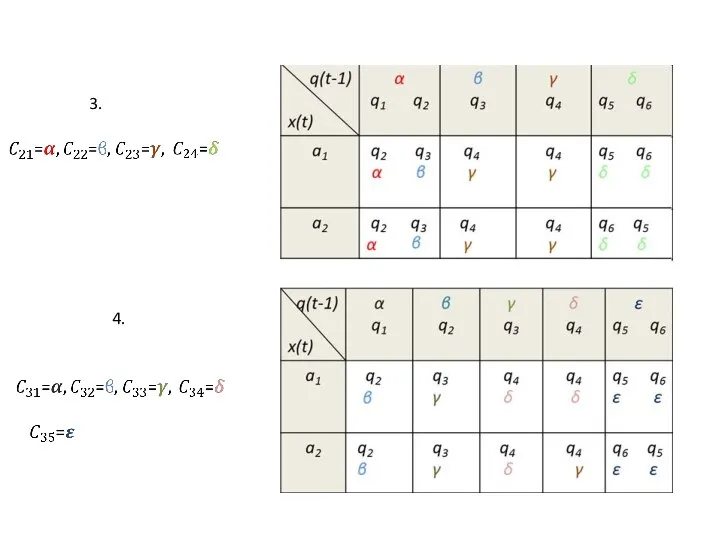
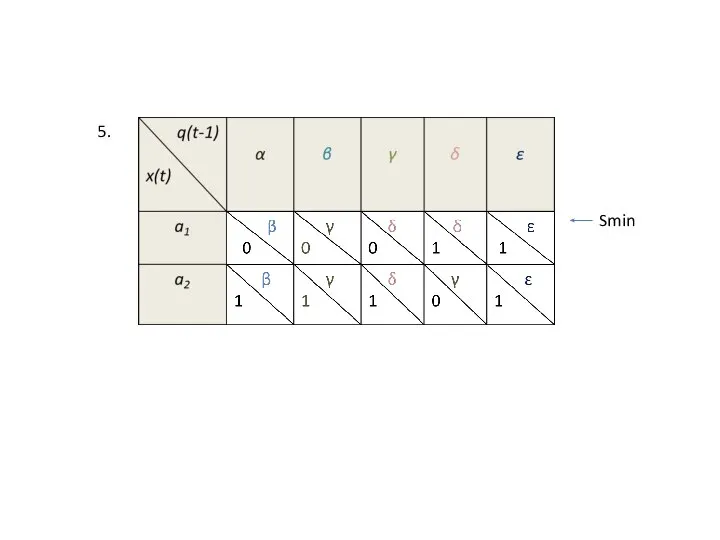
Тогда
И т.д., пока не дойдем до классов первого порядка


















 Презентация на тему Информация и информационные процессы в технике
Презентация на тему Информация и информационные процессы в технике  Односторонние T-тесты гипотез, относящихся к коэффициентам регрессии
Односторонние T-тесты гипотез, относящихся к коэффициентам регрессии Разработка информационной системы для решения задачи анализа финансовых потоков многоуровневой организации
Разработка информационной системы для решения задачи анализа финансовых потоков многоуровневой организации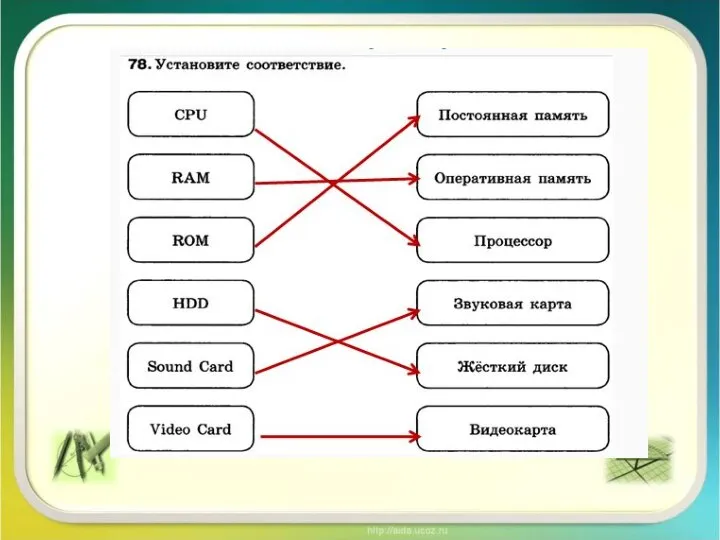 Виды памяти компьютера. Принцип работы. Урок 11
Виды памяти компьютера. Принцип работы. Урок 11 Интернет-шахматы для самообразования
Интернет-шахматы для самообразования Dynamic Host Configuration Protocol
Dynamic Host Configuration Protocol Тестирование ПО. Введение в тестирование
Тестирование ПО. Введение в тестирование Браузеры
Браузеры Информация и знания. УМК 5-7 классов
Информация и знания. УМК 5-7 классов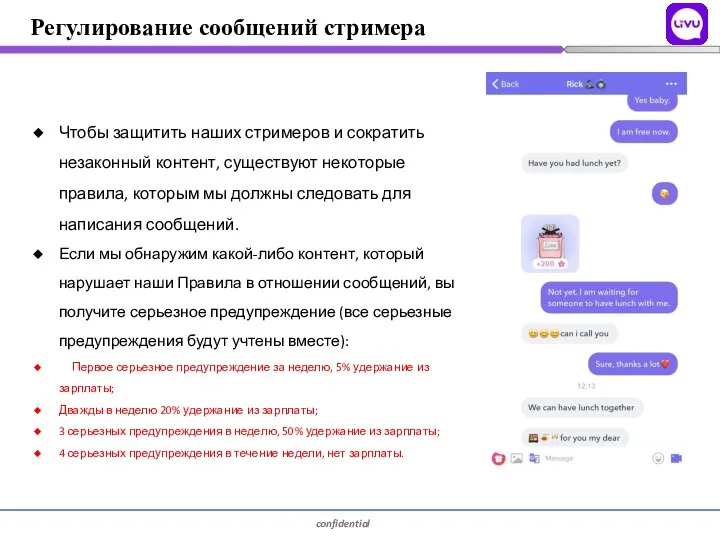 Регулирование сообщений стримера
Регулирование сообщений стримера Анализ внедрения технологии информационного моделирования в ОП Иркутск
Анализ внедрения технологии информационного моделирования в ОП Иркутск Themify Yuntsevich
Themify Yuntsevich Лекция №2. Тест-дизайн
Лекция №2. Тест-дизайн Модули метода random betavariate, sample, Random, normalvariate, gammavariate
Модули метода random betavariate, sample, Random, normalvariate, gammavariate Анализ конкретной стратегии изданий на платформах разного типа
Анализ конкретной стратегии изданий на платформах разного типа Кодирование геометрии 3D модели
Кодирование геометрии 3D модели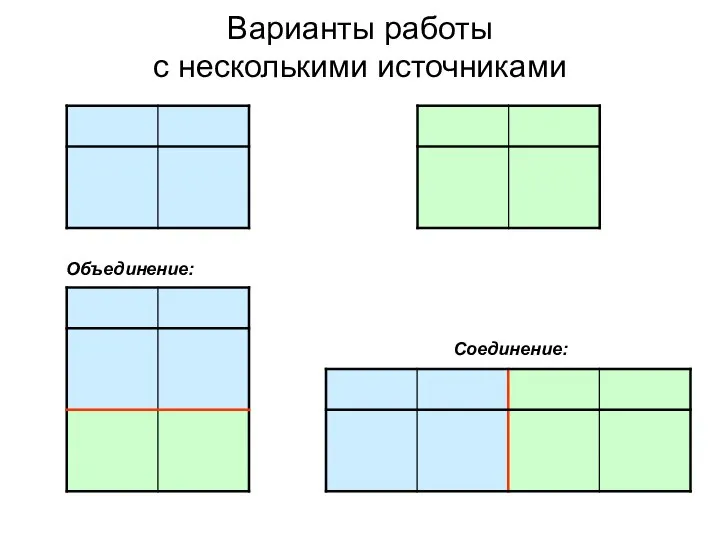 Запросы по нескольким источникам
Запросы по нескольким источникам Профсоюзные комьюнити в социальных сетях: тренды, инструменты, перспективы
Профсоюзные комьюнити в социальных сетях: тренды, инструменты, перспективы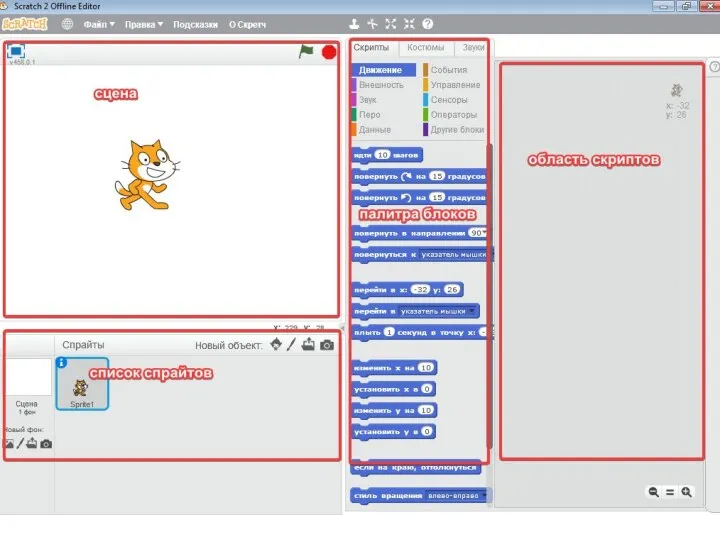 Введение. Скрипты
Введение. Скрипты Переключение контекста процесса
Переключение контекста процесса Системы счисления
Системы счисления Операционные системы. Обзор Unix-операционных систем различных производителей
Операционные системы. Обзор Unix-операционных систем различных производителей Альбом. Дипломное проектирование
Альбом. Дипломное проектирование Научная добросовестность и качество поиска и использования интеллектуальных ресурсов
Научная добросовестность и качество поиска и использования интеллектуальных ресурсов Дорожные знаки. Предписывающие знаки
Дорожные знаки. Предписывающие знаки Оценка удобства пользования сайтом завода Пластгрупп и рекомендации по внедрению доработок
Оценка удобства пользования сайтом завода Пластгрупп и рекомендации по внедрению доработок Платформа РКИ. Новый образовательный ресурс для преподавателей и иностранных студентов
Платформа РКИ. Новый образовательный ресурс для преподавателей и иностранных студентов 1. буква
1. буква