Слайд 4Способы описания алгоритмов
словесное описание;
описание алгоритма с помощью математических формул;
графическое описание алгоритма в виде

блок-схемы;
описание алгоритма с помощью псевдокода – программный;
комбинированный способ.
Слайд 5Словесное описание алгоритма
Словесное описание алгоритма представляет собой описание структуры алгоритма на естественном языке.

Достоинство: простота описания.
Недостаток: многословен и не имеет строгой формализации.
Примеры:
Слайд 6Описание алгоритма с помощью математических формул

Слайд 7Описание алгоритма с помощью псевдокода – программный
Псевдокод основан на записи алгоритмов в формализованном

представлении предписаний (спец. программы).
Достоинство: близость к языкам программирования.
Недостаток: сложность освоения и невозможность непосредственного ввода алгоритма для решения на ЭВМ.
Пример:
Слайд 8Графическое описание алгоритма в виде блок-схемы
Графический способ предполагает, что для описания структуры алгоритма

используется совокупность графических изображений (блоков), соединяемых линиями передачи управления.
Примеры:
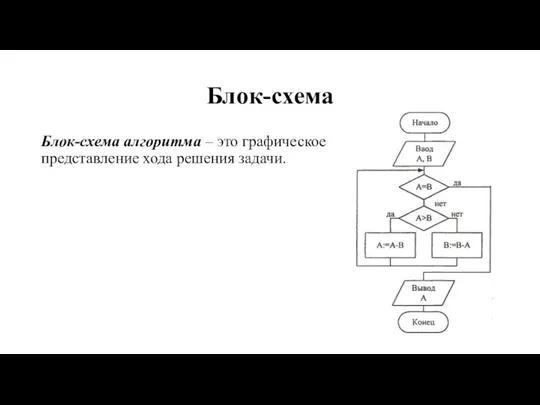
Слайд 9Блок-схема
Блок-схема алгоритма – это графическое представление хода решения задачи.
Слайд 13Пример
Разработать алгоритм вычисления гипотенузы прямоугольного треугольника по известным значениям длин его

катетов a и b.
Этап 1. Математическое описание решения задачи.
Математическим решением задачи является известная формула:
где с-длина гипотенузы, a, b – длины катетов.
Слайд 14Этап 2. Определение входных и выходных данных.
Входными данными являются значения катетов a

и b. Выходными данными является длина гипотенузы – c.
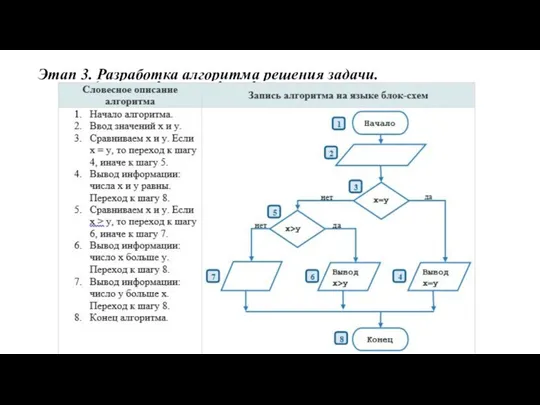
Слайд 15Этап 3. Разработка алгоритма решения задачи.

Слайд 17Пример
Разработать алгоритм вычисления наибольшего числа из двух чисел x и y.
Этап

1. Математическое описание решения задачи.
Из курса математики известно, если x > y, то наибольшее число x, если x < y, то наибольшее число y, если x = y, то число x равно числу y.
Слайд 18Этап 2. Определение входных и выходных данных.
Входными данными являются значения чисел x

и y.
Выходным данными являются:
наибольшее число
любое из чисел, если числа равны
Для решения задачи нам необходимо знать значения x и y.
Слайд 19Этап 3. Разработка алгоритма решения задачи.
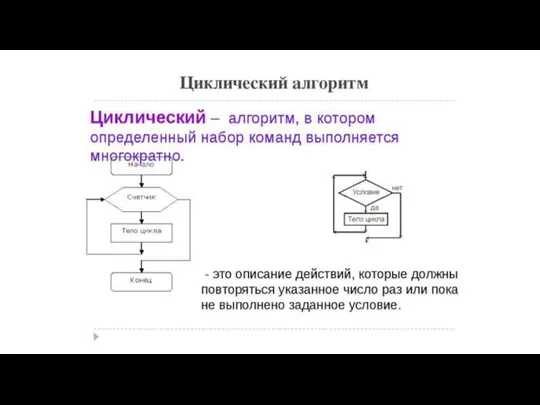
Слайд 21Циклическая структура
параметр цикла;
начальное и конечное значения параметров цикла;
шаг цикла.

Слайд 24Пример
Разработать алгоритм вычисления суммы натуральных чисел от 1 до 100.
Этап 1.

Математическое описание решения задачи.
Обозначим сумму натуральных чисел через S. Тогда формула вычисления суммы натуральных чисел от 1 до 100 может быть записана так:
где Xi – натуральное число X c номером i, который изменяется от 1 до n, n=100 – количество натуральных чисел.
Слайд 25Этап 2. Определение входных и выходных данных.
Входными данными являются натуральные числа: 1, 2,

3, 4, 5, …, 98, 99, 100.
Выходные данные – значение суммы членов последовательности натуральных чисел.
Параметр цикла – величина, определяющая количество повторений цикла. В нашем случае i – номер натурального числа.
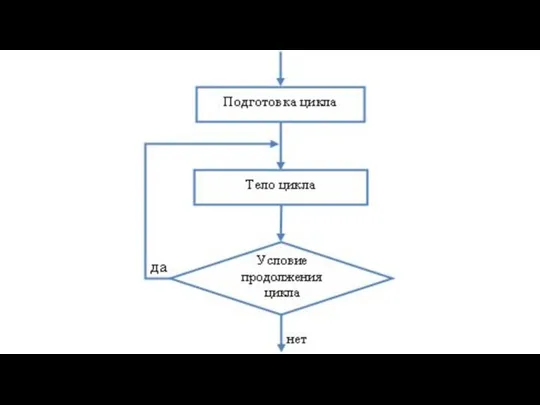
Подготовка цикла заключается в задании начального и конечного значений параметра цикла.
начальное значение параметра цикла равно 1,
конечное значение параметра цикла равно n,
шаг цикла равен 1.
Для корректного суммирования необходимо предварительно задать начальное значение суммы, равное 0.
Тело цикла. В теле цикла будет выполняться накопление значения суммы чисел, а также вычисляться следующее значение параметра цикла по формулам:
S=S+i; I=I+1;
Условие продолжения цикла: цикл должен повторяться до тех пор, пока не будет добавлен последний член последовательности натуральных чисел, т.е. пока параметр цикла будет меньше или равен конечному значению параметра цикла.
Слайд 26Этап 3. Разработка алгоритма решения задачи.

Слайд 27Задача 1
Алгоритм вычисления значения выражения K=3b+6а.

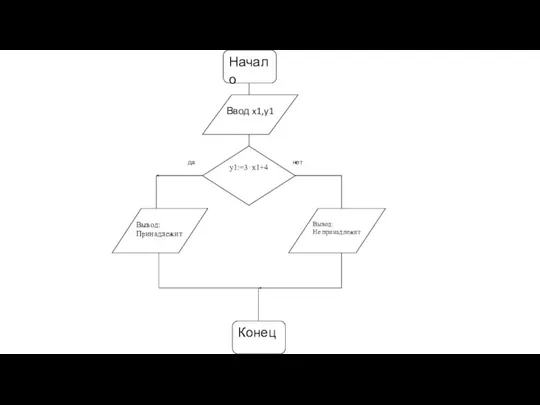
Слайд 28Задача 2
Алгоритм, определяющий, пройдет ли график функции y=3x+4 через точку с координатами

x1,y1.
Слайд 30Задача 3
Алгоритм, определяющий факториал натурального числа n:
n! = 1*2*3*….*(n-1)*n
0!=1
5!=1*2*3*4*5=120























 Создание легкой в обращении программы для отслеживания интересующих интернет-источников, и взаимодействия с ними
Создание легкой в обращении программы для отслеживания интересующих интернет-источников, и взаимодействия с ними A post office is a public facility that provides mail services. (9)
A post office is a public facility that provides mail services. (9) Работа в системе OSYM
Работа в системе OSYM Портфолио Войтович Анны
Портфолио Войтович Анны Использование Google - ресурсов при контроле знаний и умений
Использование Google - ресурсов при контроле знаний и умений Создание базы данных Access, импорт данных из Excel, связывание таблиц
Создание базы данных Access, импорт данных из Excel, связывание таблиц Складання алгоритмів з розгалуженням та повторенням. Урок 24
Складання алгоритмів з розгалуженням та повторенням. Урок 24 Разработка моделей для справочной системы по ремонту сложных узлов автомобиля
Разработка моделей для справочной системы по ремонту сложных узлов автомобиля Алгоритмы электронной подписи. Схема Эль-Гамаля
Алгоритмы электронной подписи. Схема Эль-Гамаля Продуктовый магазин. Правила проверки. Логин, пароль, аутентификация
Продуктовый магазин. Правила проверки. Логин, пароль, аутентификация Классификация мемов
Классификация мемов 3D модели
3D модели Основные теги HTML
Основные теги HTML Интегрированный урок информатики и литературы
Интегрированный урок информатики и литературы Презентація 5 клас Урок 7
Презентація 5 клас Урок 7 Шаблон создания тестов в PowerPoint
Шаблон создания тестов в PowerPoint История языков программирования: разброд и консолидация JavaScript
История языков программирования: разброд и консолидация JavaScript Функции JavaScript
Функции JavaScript Типы данных и циклы С++
Типы данных и циклы С++ Аппаратное обеспечение компьютера
Аппаратное обеспечение компьютера Проект Витрина
Проект Витрина Основи програмування
Основи програмування Электронные таблицы. Обработка числовой информации в электронных таблицах
Электронные таблицы. Обработка числовой информации в электронных таблицах Презентация ВОСП
Презентация ВОСП Аналіз моделі лісостану з континуальною розмірною структурою на основі рівнянь фон Форстера
Аналіз моделі лісостану з континуальною розмірною структурою на основі рівнянь фон Форстера Экспертные системы
Экспертные системы Pengajuan Permohonan Visa
Pengajuan Permohonan Visa МУ к КП
МУ к КП