Содержание
- 2. СИСТЕМЫ СЧИСЛЕНИЯ Система счисления – принятый способ записи чисел. В современном мире принята – десятичная система
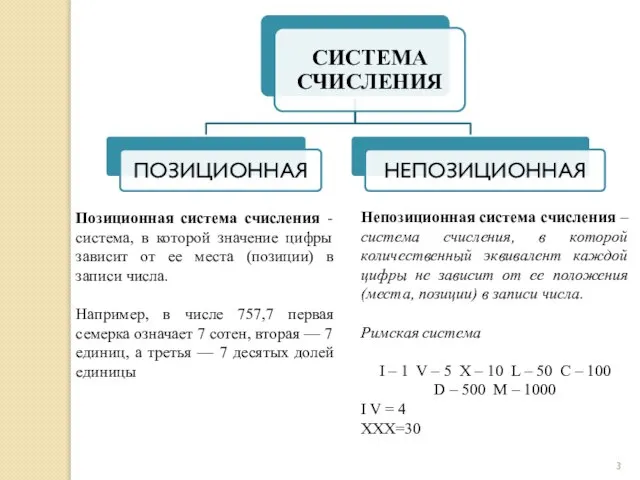
- 3. Непозиционная система счисления – система счисления, в которой количественный эквивалент каждой цифры не зависит от ее
- 4. ПРИМЕРЫ ПОЗИЦИОННЫХ СИСТЕМ СЧИСЛЕНИЯ
- 5. Основанием системы счисления называется количество знаков или символов, используемых для изображения числа в данной системе счисления.
- 6. ПРЕДСТАВЛЕНИЕ ЧИСЕЛ В РАЗНЫХ СИСТЕМАХ СЧИСЛЕНИЯ 1101(2)= 1*23 + 1*22+0*21+ 1*20; 112(3)= l*32+ 1*31 +2*30; 341,5(8)=3*82+
- 7. В каждой системе счисления цифры упорядочены в соответствии с их значениями: 1 больше 0, 2 больше
- 8. Целые числа в любой системе счисления порождаются с помощью Правила счета: Применяя это правило, запишем первые
- 9. Правило Для того чтобы число из любой системы счисления перевести в десятичную систему счисления, необходимо его
- 10. Правило перевода целых чисел из десятичной системы счисления в систему с основанием «P»: Последовательно выполнять деление
- 11. Пример перевода целого числа из десятичной системы счисления в любую другую. Переведем число 25(10) в двоичную
- 12. Правило перевода дробных чисел из десятичной системы счисления в систему с основанием «P»: Последовательно выполнять умножение
- 13. Переведем число 0,5625(10) в двоичную систему счисления 0,562510 0,5625*2=1,125 0,125*2=0,25 0,25*2=0,5 0,5*2=1,0 Таким образом, 0,5625 (10)=0,1001(2)
- 14. Правило перевода: необходимо каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр).
- 15. Правило перевода: число нужно разбить влево и вправо от запятой на триады (для восьмеричной) или тетрады
- 17. Скачать презентацию













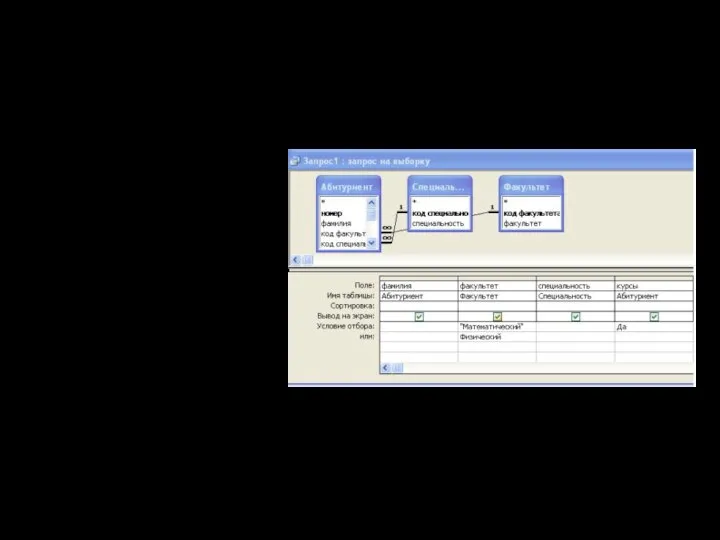 Помощь ко второй части практического задания 11 по информатике. Вид
Помощь ко второй части практического задания 11 по информатике. Вид Программные средства компьютерных коммуникаций. Назначения и классификация
Программные средства компьютерных коммуникаций. Назначения и классификация IT-квантум. ЭкоБот
IT-квантум. ЭкоБот Аутентификация и авторизация
Аутентификация и авторизация Название команды: Rework Название проекта: Redu от Re-education
Название команды: Rework Название проекта: Redu от Re-education Лети (игра)
Лети (игра) Результаты поиска литературы в электронных каталогах библиотек
Результаты поиска литературы в электронных каталогах библиотек Элементы окна программы Paint. Игра
Элементы окна программы Paint. Игра Алгоритм Ветвление. Трассировка
Алгоритм Ветвление. Трассировка Организация рабочих мест сотрудника ЗИ
Организация рабочих мест сотрудника ЗИ Разработка системы управления взаимоотношениями с клиентами-CRM на примере
Разработка системы управления взаимоотношениями с клиентами-CRM на примере Множества. Изучение алгоритмизации и основ программирования на языке Python в курсе Информатика и ИКТ
Множества. Изучение алгоритмизации и основ программирования на языке Python в курсе Информатика и ИКТ Переменные
Переменные Способы создания и продвижения новостей в медиа
Способы создания и продвижения новостей в медиа Способы записи алгоритмов
Способы записи алгоритмов Протокол IPv6. Вычислительные сети и коммуникации
Протокол IPv6. Вычислительные сети и коммуникации Персональные компьютеры и приложения
Персональные компьютеры и приложения Алгоритмы и модели трассировки печатных соединений в ЭА
Алгоритмы и модели трассировки печатных соединений в ЭА Студенческое объединение Камчатка представляет
Студенческое объединение Камчатка представляет Семисегментный индикатор
Семисегментный индикатор Как обеспечить 100% возврат первичных документов и сохранить нервы при проверках
Как обеспечить 100% возврат первичных документов и сохранить нервы при проверках Reigister on the PCH website
Reigister on the PCH website Разработка таблицы с расчетами
Разработка таблицы с расчетами Рисуем торт
Рисуем торт Пошаговая инструкция по работе с цифровой платформой
Пошаговая инструкция по работе с цифровой платформой Разработка календарного плана в MS Project 2007-2010
Разработка календарного плана в MS Project 2007-2010 Телевидение как искусство и средство коммуникации
Телевидение как искусство и средство коммуникации Перемещение объектов. Урок 6
Перемещение объектов. Урок 6