Системы счисления. Способы представления чисел

Система счисления
Система счисления – это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами. Системы счисления делятся на непозиционные и позиционные.

Типы систем счисления
Непозиционная система счисления – это система, в которой значение символа не зависит от его положения в числе. Примером непозиционной системы счисления может служить римская система счисления, в которой цифры обозначаются различными знаками: Ⅰ – 1, Ⅲ – 3, Ⅵ – 6, L – 50 …

Типы систем счисления
Позиционная система счисления – это система, в которой значение символа зависит от его места (позиции) в ряду цифр, изображающих число.

Алфавит системы счисления
Алфавит системы счисления – это совокупность цифр и букв, с помощью которых записываются числа

Основание системы счисления
Система счисления – это количество цифр в алфавите

Виды систем счисления
Двоичная система
Восьмеричная система
Десятичная система
Шестнадцатеричная система

Двоичная система счисления
Двоичная система счисления – основание S=2. Для записи числа используются две цифры: 0 и 1. При этом каждый старший разряд больше соседнего младшего в два раза. Любое число в двоичной системе счисления представляется в виде суммы целых степеней основания S=2, умноженных на соответствующие коэффициенты (0 или 1).

Восьмеричная система счисления
Восьмеричная система счисления – основание S=8.
Используются цифры: 0, 1, 2, …, 7. Любое число представляется суммой целых степеней основания S=8, умноженных на соответствующие коэффициенты ai=0, …, 7.

Десятичная система счисления
Десятичная система счисления – основание S=10.
Набор цифр этой системы 0, 1, 2, …, 9. Любое целое число в десятичной системе счисления записывается как сумма величин: 100, 101, 102, …, каждая из которых может быть взята от 1 до 9 раз.

Шестнадцатеричная система счисления
Шестнадцатеричная система счисления – основание S=16.
Алфавит цифровых знаков состоит из 16-ти символов: первые десять – арабские цифры от 0 до 9 и дополнительные – A(10), B(11), C(12), D(13), E(14), F(15).

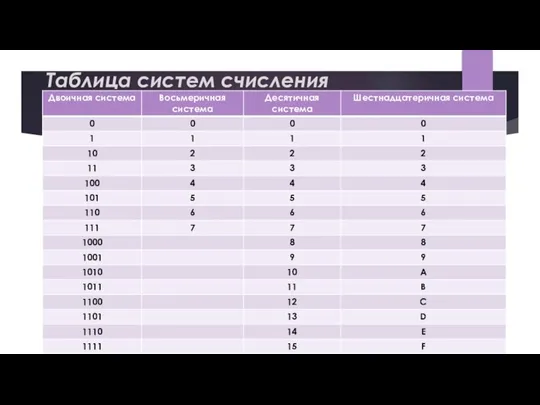
Таблица систем счисления

Переводы из десятичной системы счисления
Сначала производится последовательное деление столбиком исходного числа и получаемых (от предыдущих делений) частных (больших или равных основанию) на основание новой системы счисления и записываются остатки от делений. Деление продолжается до тех пор, пока частное не станет меньше основания. Затем выписываются цифры в новой системе счисления вместо (полученных в десятичной системе счисления) последнего частного и остатков от делений в обратном (получению) порядке.
Полученное число является записью исходного числа в новой системе счисления.

Переводы из десятичной системы счисления

Переводы в десятичную систему
Считается сумма произведений цифр исходной системы счисления (предварительно переведённых в десятичную систему счисления) на веса разрядов (основание системы счисления в степени номер разряда, начиная с нулевого) в исходной системе.
Полученное число является записью исходного числа в десятичной системе счисления.

Переводы в десятичную систему счисления

Исходное число двоичной системы счисления разбивается на триады (тройки цифр двоичной системы счисления), начиная с цифры единиц (самой правой). Последняя (самая левая) триада может быть неполной, тогда в неё слева добавляется цифра 0 (одна или две). Затем триады заменяются на соответствующие (по таблице триад) цифры восьмеричной системы счисления.
Пример: 10110011111² = 010 110 011 111² =2637 и в обратном направлении
Перевод из двоичной системы в восьмеричную

Перевод из двоичной системы в шестнадцатеричную
Исходное число двоичной системы счисления разбивается на тетрады (четвёрки цифр двоичной системы счисления), начиная с цифры единиц (самой правой). Последняя (самая левая) тетрада может быть неполной, тогда в неё слева добавляется цифра 0 (одна, две или три). Затем тетрады заменяются на соответствующие (по таблице тетрад) цифры шестнадцатеричной системы счисления.
Пример: 10110011111² = 0101 1001 1111² =59F и в обратном направлении