«Старинные системы записи чисел» Составила: Барышева Маргарита, обучающаяся 7 класса. Руководитель: Медведева Елена Валерьевна,
Содержание
- 2. Так говорили пифагорейцы, подчёркивая необычайно важную роль чисел в практической деятельности.
- 3. Люди всегда считали и записывали числа, даже пять тысяч лет назад. Но записывали они их по
- 4. Что есть число? Число – это некоторая величина
- 5. Числа складываются из цифр по особым правилам. На разных этапах развития человечества, у разных народов эти
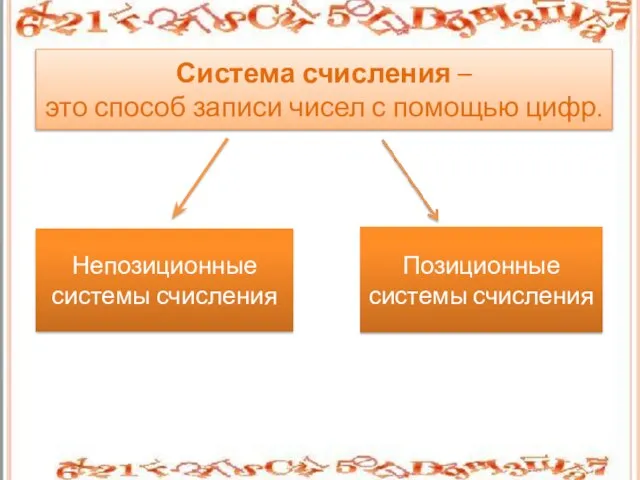
- 6. Позиционные системы счисления Система счисления – это способ записи чисел с помощью цифр. Непозиционные системы счисления
- 7. Непозиционные системы счисления - количественные значения символов, используемых для записи чисел, не зависят от их места
- 8. Единичная непозиционная система счисления 10 - 11 тысяч лет до н.э., когда у людей появилась потребность
- 9. Древнеегипетская десятичная непозиционная система счисления Древнеегипетская десятичная непозиционная система счисления возникла во второй половине третьего тысячелетия
- 10. Алфавитная непозиционная система счисления Древней Греции Наряду с иероглифическими знаками в древности широко применялись алфавитные системы
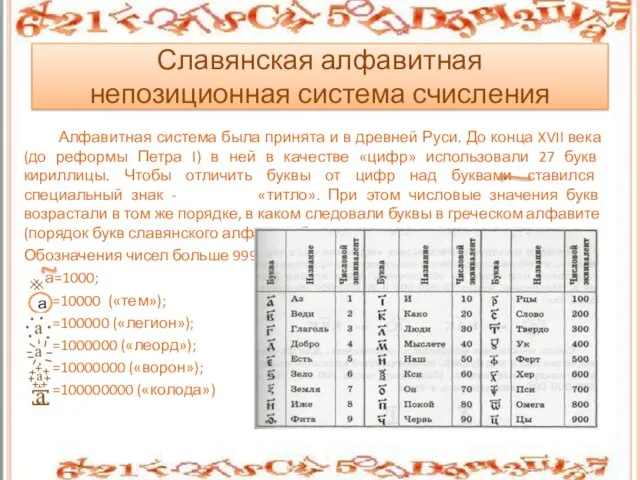
- 11. Алфавитная система была принята и в древней Руси. До конца XVII века (до реформы Петра I)
- 12. Римская непозиционная система счисления Римские числа являются примером полупозиционной системы образования числа, которая сохранилась до наших
- 13. Иероглифические и алфавитные системы счисления имели один существенный недостаток – в них было очень трудно выполнять
- 14. Индийская мультипликативная система счисления; Вавилонская система счисления; Десятичная система счисления. Старинные позиционные системы счисления - количественные
- 15. Вавилонская система счисления Идея приписывать цифрам разные величины в зависимости от того, какую позицию они занимают
- 16. Десятичная система счисления Современная десятичная система счисления возникла приблизительно в V веке н. э. в Индии.
- 17. Простота выполнения арифметических операций; Ограниченное количество символов, необходимых для записи чисел; Удобна для механического представления чисел.
- 19. Скачать презентацию














 Форсаж 2018
Форсаж 2018 Организация работы локальной сети. Стек протоколов TCP/IP
Организация работы локальной сети. Стек протоколов TCP/IP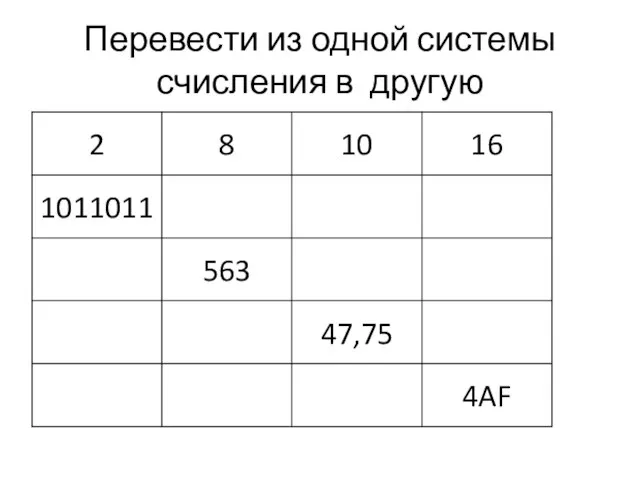 Перевод из одной системы счисления в другую
Перевод из одной системы счисления в другую Инфомагия. Игра (8 класс)
Инфомагия. Игра (8 класс) Создание модели компьютерного класса будущего
Создание модели компьютерного класса будущего Единое информационное пространство в сфере культуры
Единое информационное пространство в сфере культуры Моделирование, как метод познания
Моделирование, как метод познания Мосты. Прозрачные мосты. Транслирующие и инкапсулирующие мосты
Мосты. Прозрачные мосты. Транслирующие и инкапсулирующие мосты Интернет и английский язык: что нужно знать пользователю подростку
Интернет и английский язык: что нужно знать пользователю подростку Введение в объекты Java
Введение в объекты Java Game Studies, уличная фотография в видеоиграх
Game Studies, уличная фотография в видеоиграх ИК Базы данных. Урок 6. Презентация
ИК Базы данных. Урок 6. Презентация SDSM. Sample distribution shadow maps
SDSM. Sample distribution shadow maps Задача и SPARQL-запрос
Задача и SPARQL-запрос Creating Internet applications. HTML Technology
Creating Internet applications. HTML Technology Информационные технологии комплектации заказов в логистике
Информационные технологии комплектации заказов в логистике Устройства ввода графической информации. Итоговое тестирование
Устройства ввода графической информации. Итоговое тестирование Advent Empire. Карьерная лестница
Advent Empire. Карьерная лестница Информационная система диагностики оборудования электродегидратора
Информационная система диагностики оборудования электродегидратора Изобретатель Приложений. Урок 6
Изобретатель Приложений. Урок 6 Классификация программного обеспечения
Классификация программного обеспечения Операционные системы их виды и функции
Операционные системы их виды и функции Основы сетевых технологий_Лекция 3
Основы сетевых технологий_Лекция 3 Версионное хранение данных
Версионное хранение данных Хранение информации
Хранение информации Табличные информационные модели
Табличные информационные модели Братья Гримм. Сказки
Братья Гримм. Сказки Основы_CSS_D74VJtP
Основы_CSS_D74VJtP