Тема 2.1.2

Сжатие данных
Алгоритмическое преобразование данных, производимое с целью уменьшения занимаемого ими объёма

КОЭФФИЦИЕНТ СЖАТИЯ
СООТНОШЕНИЕ ИСХОДНОГО И СЖАТОГО ФАЙЛА

АЛГОРИТМ RLE
КОДИРОВАНИЕ ЦЕПОЧЕК ОДИНАКОВЫХ СИМВОЛОВ
100
100
200 байтов
Файл qq.txt
Файл qq.rle (сжатый)
4 байта

КОДИРОВАНИЕ ШЕННОНА — ФАНО
АЛГОРИТМ ПРЕФИКСНОГО НЕОДНОРОДНОГО КОДИРОВАНИЯ. ОТНОСИТСЯ К ВЕРОЯТНОСТНЫМ МЕТОДАМ СЖАТИЯ.
ИСПОЛЬЗУЕТ ИЗБЫТОЧНОСТЬ СООБЩЕНИЯ, ЗАКЛЮЧЁННУЮ В НЕОДНОРОДНОМ РАСПРЕДЕЛЕНИИ ЧАСТОТ СИМВОЛОВ ЕГО (ПЕРВИЧНОГО) АЛФАВИТА, ТО ЕСТЬ ЗАМЕНЯЕТ КОДЫ БОЛЕЕ ЧАСТЫХ СИМВОЛОВ КОРОТКИМИ ДВОИЧНЫМИ ПОСЛЕДОВАТЕЛЬНОСТЯМИ, А КОДЫ БОЛЕЕ РЕДКИХ СИМВОЛОВ — БОЛЕЕ ДЛИННЫМИ ДВОИЧНЫМИ ПОСЛЕДОВАТЕЛЬНОСТЯМИ.

ОСНОВНЫЕ ЭТАПЫ АЛГОРИТМА ШЕННОНА — ФАНО
СИМВОЛЫ ПЕРВИЧНОГО АЛФАВИТА M1 ВЫПИСЫВАЮТ ПО УБЫВАНИЮ ВЕРОЯТНОСТЕЙ.
СИМВОЛЫ ПОЛУЧЕННОГО АЛФАВИТА ДЕЛЯТ НА ДВЕ ЧАСТИ, СУММАРНЫЕ ВЕРОЯТНОСТИ СИМВОЛОВ КОТОРЫХ МАКСИМАЛЬНО БЛИЗКИ ДРУГ ДРУГУ.
В ПРЕФИКСНОМ КОДЕ ДЛЯ ПЕРВОЙ ЧАСТИ АЛФАВИТА ПРИСВАИВАЕТСЯ ДВОИЧНАЯ ЦИФРА «0», ВТОРОЙ ЧАСТИ — «1».
ПОЛУЧЕННЫЕ ЧАСТИ РЕКУРСИВНО ДЕЛЯТСЯ И ИХ ЧАСТЯМ НАЗНАЧАЮТСЯ СООТВЕТСТВУЮЩИЕ ДВОИЧНЫЕ ЦИФРЫ В ПРЕФИКСНОМ КОДЕ.

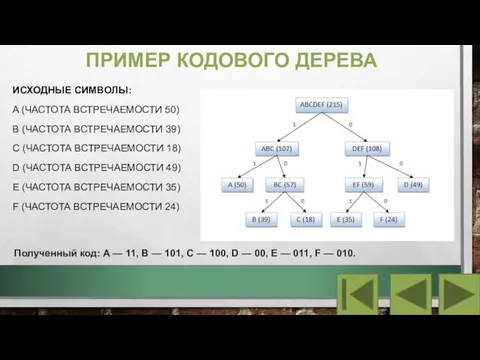
ПРИМЕР КОДОВОГО ДЕРЕВА
ИСХОДНЫЕ СИМВОЛЫ:
A (ЧАСТОТА ВСТРЕЧАЕМОСТИ 50)
B (ЧАСТОТА ВСТРЕЧАЕМОСТИ 39)
C (ЧАСТОТА ВСТРЕЧАЕМОСТИ 18)
D (ЧАСТОТА ВСТРЕЧАЕМОСТИ 49)
E (ЧАСТОТА ВСТРЕЧАЕМОСТИ 35)
F (ЧАСТОТА ВСТРЕЧАЕМОСТИ 24)
Полученный код: A — 11, B — 101, C — 100, D — 00, E — 011, F — 010.

КОД ШЕННОНА-ФАНО
ДОСТОИНСТВА И НЕДОСТАТКИ
учитывается частота символов
не нужен символ-разделитель
код префиксный – можно декодировать по мере поступления данных
нужно заранее знать частоты символов
код неоптимален
при ошибке в передаче сложно восстановить «хвост»
не учитывает повторяющиеся последовательности символов

АЛГОРИТМ ХАФФМАНА
АЛГОРИТМ ОПТИМАЛЬНОГО ПРЕФИКСНОГО КОДИРОВАНИЯ АЛФАВИТА С МИНИМАЛЬНОЙ ИЗБЫТОЧНОСТЬЮ
ЭТОТ МЕТОД КОДИРОВАНИЯ СОСТОИТ ИЗ ДВУХ ОСНОВНЫХ ЭТАПОВ:
ПОСТРОЕНИЕ ОПТИМАЛЬНОГО КОДОВОГО ДЕРЕВА.
ПОСТРОЕНИЕ ОТОБРАЖЕНИЯ КОД-СИМВОЛ НА ОСНОВЕ ПОСТРОЕННОГО ДЕРЕВА.

КЛАССИЧЕСКИЙ АЛГОРИТМ ХАФФМАНА НА ВХОДЕ ПОЛУЧАЕТ ТАБЛИЦУ ЧАСТОТ ВСТРЕЧАЕМОСТИ СИМВОЛОВ В СООБЩЕНИИ. ДАЛЕЕ НА ОСНОВАНИИ ЭТОЙ ТАБЛИЦЫ СТРОИТСЯ ДЕРЕВО КОДИРОВАНИЯ ХАФФМАНА (Н-ДЕРЕВО).
СИМВОЛЫ ВХОДНОГО АЛФАВИТА ОБРАЗУЮТ СПИСОК СВОБОДНЫХ УЗЛОВ. КАЖДЫЙ ЛИСТ ИМЕЕТ ВЕС, КОТОРЫЙ МОЖЕТ БЫТЬ РАВЕН ЛИБО ВЕРОЯТНОСТИ, ЛИБО КОЛИЧЕСТВУ ВХОЖДЕНИЙ СИМВОЛА В СЖИМАЕМОЕ СООБЩЕНИЕ.
ВЫБИРАЮТСЯ ДВА СВОБОДНЫХ УЗЛА ДЕРЕВА С НАИМЕНЬШИМИ ВЕСАМИ.
СОЗДАЕТСЯ ИХ РОДИТЕЛЬ С ВЕСОМ, РАВНЫМ ИХ СУММАРНОМУ ВЕСУ.
РОДИТЕЛЬ ДОБАВЛЯЕТСЯ В СПИСОК СВОБОДНЫХ УЗЛОВ, А ДВА ЕГО ПОТОМКА УДАЛЯЮТСЯ ИЗ ЭТОГО СПИСКА.
ОДНОЙ ДУГЕ, ВЫХОДЯЩЕЙ ИЗ РОДИТЕЛЯ, СТАВИТСЯ В СООТВЕТСТВИЕ БИТ 1, ДРУГОЙ — БИТ 0. БИТОВЫЕ ЗНАЧЕНИЯ ВЕТВЕЙ, ИСХОДЯЩИХ ОТ КОРНЯ, НЕ ЗАВИСЯТ ОТ ВЕСОВ ПОТОМКОВ.
ШАГИ, НАЧИНАЯ СО ВТОРОГО, ПОВТОРЯЮТСЯ ДО ТЕХ ПОР, ПОКА В СПИСКЕ СВОБОДНЫХ УЗЛОВ НЕ ОСТАНЕТСЯ ТОЛЬКО ОДИН СВОБОДНЫЙ УЗЕЛ. ОН И БУДЕТ СЧИТАТЬСЯ КОРНЕМ ДЕРЕВА.

ПРИМЕР
ИСХОДНЫЕ СИМВОЛЫ:
Полученный код:

АЛГОРИТМ ХАФФМАНА
ДОСТОИНСТВА И НЕДОСТАТКИ
код оптимальный среди алфавитных кодов
нужно заранее знать частоты символов
при ошибке в передаче сложно восстановить «хвост»
не учитывает повторяющиеся последовательности символов

АЛГОРИТМ LZW
Этот метод позволяет достичь одну из наилучших степеней сжатия среди других существующих методов сжатия графических данных, при полном отсутствии потерь или искажений в исходных файлах. В настоящее время используется в файлах формата TIFF, PDF, GIF, PostScript и других, а также отчасти во многих популярных программах сжатия данных (ZIP, ARJ, LHA).

КОДИРОВАНИЕ
Начало.
Шаг 1. Все возможные символы заносятся в словарь. Во входную фразу X заносится первый символ сообщения.
Шаг 2. Считать очередной символ Y из сообщения.
Шаг 3. Если Y — это символ конца сообщения, то выдать код для X, иначе:
Если фраза XY уже имеется в словаре, то присвоить входной фразе значение XY и перейти к Шагу 2 ,
Иначе выдать код для входной фразы X, добавить XY в словарь и присвоить входной фразе значение Y. Перейти к Шагу 2.
Конец.

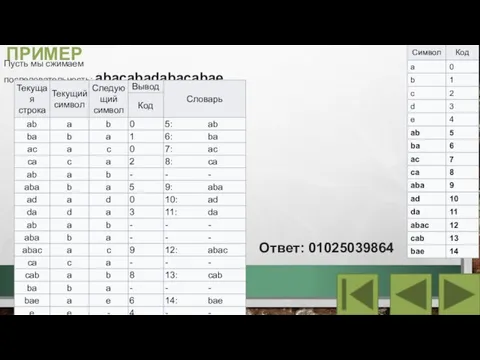
ПРИМЕР
Пусть мы сжимаем последовательность: abacabadabacabae.
Ответ: 01025039864

ДЕКОДИРОВАНИЕ
Начало.
Шаг 1. Все возможные символы заносятся в словарь. Во входную фразу X заносится первый код декодируемого сообщения.
Шаг 2. Считать очередной код Y из сообщения.
Шаг 3. Если Y — это конец сообщения, то выдать символ, соответствующий коду X, иначе:
Если фразы под кодом XY нет в словаре, вывести фразу, соответствующую коду X, а фразу с кодом XY занести в словарь.
Иначе присвоить входной фразе код XY и перейти к Шагу 2 .
Конец.

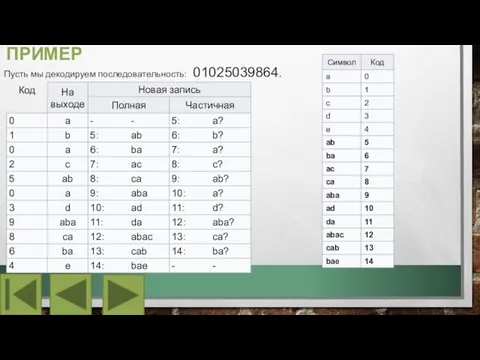
ПРИМЕР
Пусть мы декодируем последовательность: 01025039864.