Целые числа. Метод координат. Прямоугольная система координат на плоскости. Введение в программирование для начинающих

ЦЕЛЬ ЗАНЯТИЯ
Изучить целые числа числа.
Ознакомиться с прямоугольной системой координат.
Определять координаты точки, отмеченной на координатной плоскости.
Научиться строить точки по заданным её координатам.

ЦЕЛЫЕ ЧИСЛА

ЦЕЛЫЕ ЧИСЛА
5-2=3; -натуральное число 2-5=- 3; - отрицательное число
а, -а - противоположные числа
Между натуральными и отрицательными числами находится число «0»
а+0=а; а+(-а)=0;
N- множество натуральных чисел
Z- множество целых чисел

СРАВНЕНИЕ ЦЕЛЫХ ЧИСЕЛ
1<2<3<4<5<….
Из двух целых чисел меньше то, изображение которого лежит на числовой прямой левее другого.
| | - абсолютная величина.
|а|=а |-а|=а |0|=0
Отрицательное число меньше «0».
«0» меньше положительного числа.
Из двух отрицательных чисел меньше то, у которого больше отрицательная величина.
-5<0 -10<-5 -5<3

ПРАВИЛА СЛОЖЕНИЯ, ВЫЧИТАНИЯ, УМНОЖЕНИЯ И ДЕЛЕНИЯ
При сложении двух положительных или двух отрицательных чисел, складывают их абсолютные величины и приписывают сумме тот же знак.
2+5=7 -2 + (-5)= -7
При сложении чисел с разными знаками, от большей абсолютной величины отнимают меньшую приписывают сумме знак числа большей абсолютной величины.
-5+3=-2 5+(-3)=2
Вычитание можно заменить сложением
-5-3= -5+(-3)= -8 3-5=3+(-5)=-2 3-(-5)=8

ПРАВИЛА СЛОЖЕНИЯ, ВЫЧИТАНИЯ, УМНОЖЕНИЯ И ДЕЛЕНИЯ
Произведение и частное двух чисел с одинаковыми знаками положительно.
Произведение и частное двух чисел с разными знаками отрицательно.
(-2)*(-2)= 4 (-4):(-2)= 2
(-2)* 3=- 6 (-4): 2= -2

МЕТОД КООРДИНАТ. ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ НА ПЛОСКОСТИ

ОПРЕДЕЛЕНИЕ КООРДИНАТЫ
Координаты— это набор данных, по которому определяется положение того или иного объекта.

ДЕКАРТОВА СИСТЕМА КООРДИНАТ
Французский математик Рене Декарт (1596–1650) предложил задавать положение точки на плоскости с помощью двух координат.

СИСТЕМА КООРДИНАТ
Система координат —это две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является началом отсчёта для каждой из них.
Совокупность чисел, определяющих положение конкретной точки, называется координатами
этой точки.

СИСТЕМА КООРДИНАТ
Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве.
Декартовой обычно называют прямоугольную систему координат с одинаковыми масштабами по осям.

ДЕКАРТОВА СИСТЕМА КООРДИНАТ
ось абсцисс
ось ординат

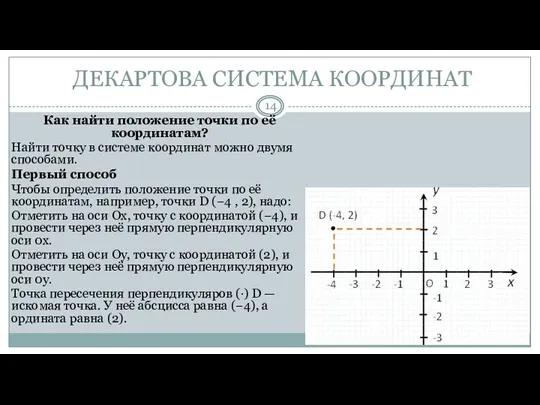
ДЕКАРТОВА СИСТЕМА КООРДИНАТ
Как найти положение точки по её координатам?
Найти точку в системе координат можно двумя способами.
Первый способ
Чтобы определить положение точки по её координатам, например, точки D (−4 , 2), надо:
Отметить на оси Ox, точку с координатой (−4), и провести через неё прямую перпендикулярную оси 0x.
Отметить на оси Oy, точку с координатой (2), и провести через неё прямую перпендикулярную оси 0y.
Точка пересечения перпендикуляров (·) D — искомая точка. У неё абсцисса равна (−4), а ордината равна (2).

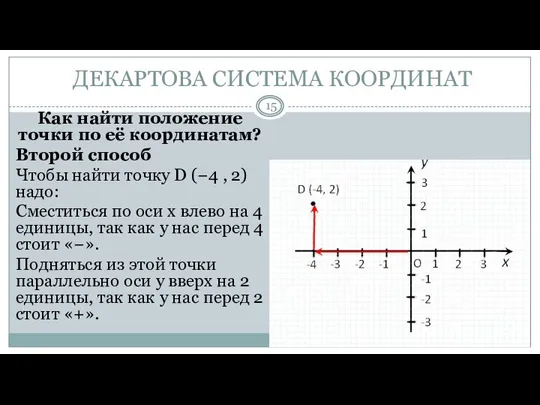
ДЕКАРТОВА СИСТЕМА КООРДИНАТ
Как найти положение точки по её координатам?
Второй способ
Чтобы найти точку D (−4 , 2) надо:
Сместиться по оси x влево на 4 единицы, так как у нас перед 4 стоит «−».
Подняться из этой точки параллельно оси y вверх на 2 единицы, так как у нас перед 2 стоит «+».

ДЕКАРТОВА СИСТЕМА КООРДИНАТ
Расшифровать фразу :
«Лучше один раз увидеть, чем сто раз услышать»