Устройство учебной модели компьютера “Е97”

Происхождение
Автор хотел обобщить основные принципы работы современных ЭВМ и разработать новую модель, которая с одной стороны проста и наглядна, а с другой — способна заменить собой при обучении реальную ЭВМ. Модель получила краткое название "Е97"

Структура памяти
Память двух видов - оперативная(ОЗУ) и постоянная(ПЗУ).
В первой хранится текущая информация по решаемой задаче, причем она может как считываться, так и записываться.
Во второй, предназначенной только для считывания, содержатся
разработанные при проектировании ЭВМ подпрограммы.

Организация данных
Минимальной адресуемой ячейкой памяти в современных
ЭВМ является байт. Все байты в памяти "Е97" пронумерованы и их 16-разрядные номера находятся в пределах от 0000 до FFFF.

Структура процессора
16-разрядный процессор "Е97", способен работать как с двухбайтовыми словами, так и с отдельными байтами. В процессоре имеются внутренние регистры памяти,
при помощи которых реализован метод косвенной адресации
к ОЗУ. Полное 16-разрядное адресное
пространство "Е97" позволяет напрямую адресовать до 64
Кбайт памяти.

Способы адресации команд
Регистровый метод адресации: операнд является содержимым указанного регистра;
Метод косвенной адресации: операндом является содержимое ячейки ОЗУ, адрес которой задан в указанном регистре;
Резерв; возможно, в будущих версиях здесь будет реализован индексный метод адресации;
Адресация по PC: операнд извлекается с использованием информации, входящей в команду.

Система команд процессора
1 – перепись
2 – сложение
3 – вычитание
4 – сравнение
5 – умножение
6 – деление
7 – логическое "И"
8 – ИЛИ
9 – ИСКЛЮЧАЮЩЕЕ ИЛИ
A – ввод из порта
B – вывод из порта.

Примеры программ на языке процессора

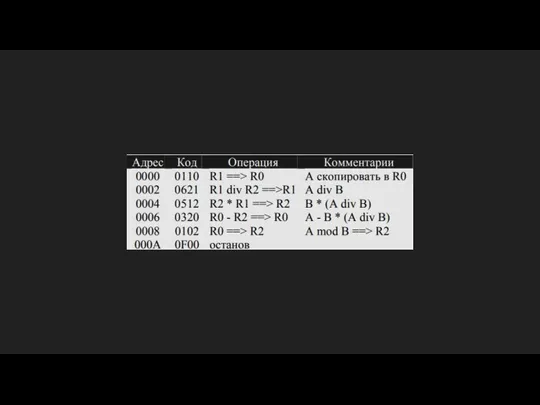
ПРИМЕР 1. ОСТАТОК ОТ ДЕЛЕНИЯ
Целые числа A и B хранятся в регистрах R1 и R2. Вычислить результат деления нацело A div B и остаток от деления A mod B, поместив результаты в регистры R1 и R2 соответственно.
РЕШЕНИЕ. Для деления нацело в "Е97" существует специальная команда. Что касается остатка от деления, то его можно вычислить по формуле
A mod B = A - B * (A div B)
При вычислениях для хранения промежуточных результатов используется регистр R0.

ПРИМЕР 2. ПОВЕРХНОСТЬ ПАРАЛЛЕЛЕПИПЕДА.
Вычислить полную поверхность параллелепипеда со сторонами A, B и C. Считать, что исходные значения находятся в ячейках ОЗУ. Результат также поместить в ячейку.
РЕШЕНИЕ. Как известно, полная поверхность параллелепипеда вычисляется по формуле
S = 2 * (A * B + A * C + B * C)
Для упрощения программы, выражение удобно представить в виде
S = 2 * [A * (B + C) + B * C]
Запомним на будущее, что преобразование исходного выражения часто позволяет заметно сократить программу.