Способы преобразования чертежа. Лекция 4

Основные способы преобразования
Способ перемены (замены) плоскостей проекций
Способ плоскопараллельного перемещения
Способ вращения вокруг проецирующих прямых
Способ вращения вокруг линий уровня

ЧЕТЫРЕ ОСНОВНЫЕ ЗАДАЧИ, РЕШАЕМЫЕ СПОСОБАМИ ПРЕОБРАЗОВАНИЯ
ПРЕОБРАЗОВАТЬ ПРЯМУЮ ОБЩЕГО ПОЛОЖЕНИЯ В ПРЯМУЮ ЧАСТНОГО ПОЛОЖЕНИЯ (ГОРИЗОНТАЛЬ ИЛИ ФРОНТАЛЬ)
ПРЕОБРАЗОВАТЬ ПРЯМУЮ ЧАСТНОГО ПОЛОЖЕНИЯ В ПРОЕЦИРУЮЩУЮ ПРЯМУЮ
ПРЕОБРАЗОВАТЬ ПЛОСКОСТЬ ОБЩЕГО ПОЛОЖЕНИЯ В ПРОЕЦИРУЮЩУЮ ПЛОСКОСТЬ
4. ПРЕОБРАЗОВАТЬ ПЛОСКОСТЬ ПРОЕЦИРУЮЩУЮ В ПЛОСКОСТЬ УРОВНЯ

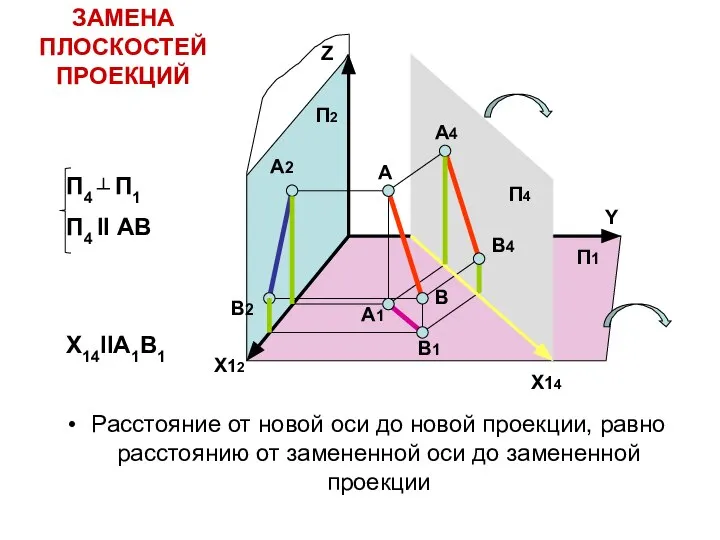
Расстояние от новой оси до новой проекции, равно расстоянию от замененной оси до замененной проекции
Y
X12
Z
А
В
А1
В1
А2
В2
В4
А4
X14
П4
П1
П2
ЗАМЕНА ПЛОСКОСТЕЙ ПРОЕКЦИЙ
П4 ┴ П1
П4 II АВ
X14IIA1B1

Позиционная задача
Определить углы наклона прямой к горизонтальной и фронтальной плоскостям проекций, если А(15,40,10); В(65,30,15).
Задачу решить способом замены плоскостей проекций
(φ и ψ)

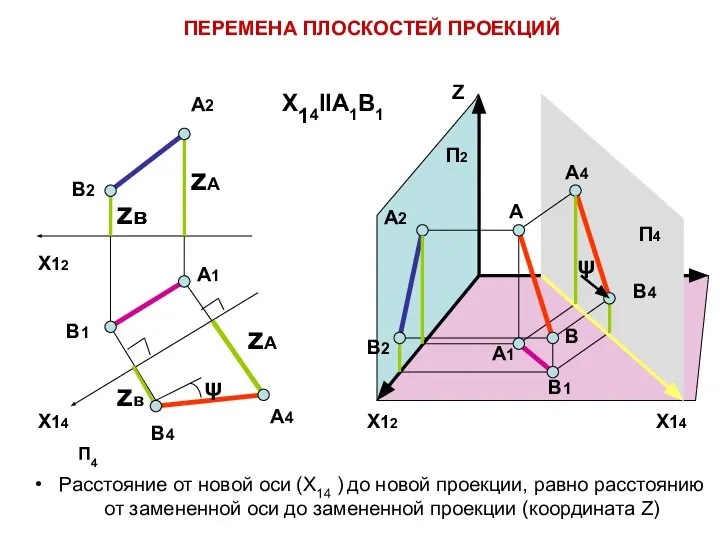
ПЕРЕМЕНА ПЛОСКОСТЕЙ ПРОЕКЦИЙ
А1
В1
А2
В2
В4
А4
X12
Z
А
В
А1
В1
А2
В2
В4
А4
X14
П4
П2
X12
X14
Расстояние от новой оси (X14 ) до новой проекции, равно расстоянию от замененной оси до замененной проекции (координата Z)
ψ
zв
zв
zА
zА
ψ
X14IIA1B1
П4

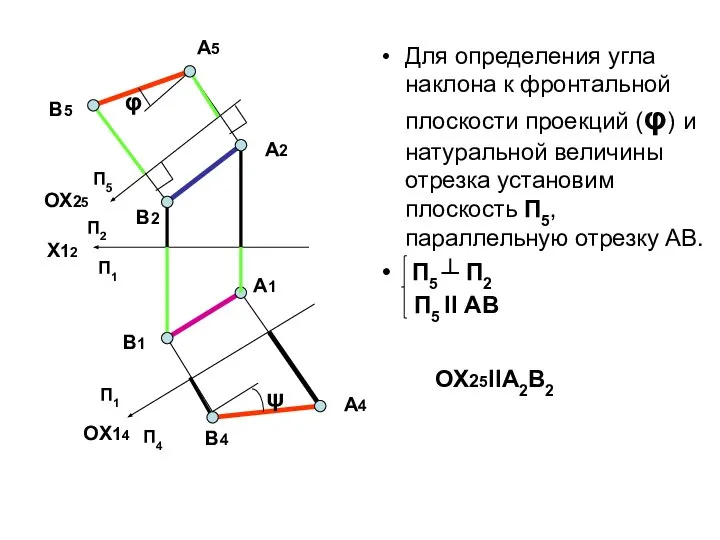
Для определения угла наклона к фронтальной плоскости проекций (φ) и натуральной величины отрезка установим плоскость П5, параллельную отрезку АВ.
П5 ┴ П2
П5 II АВ
А1
В1
А2
В2
В4
А4
X12
ОX14
ψ
А5
ОX25
В5
φ
ОX25IIA2B2
П5
П4
П1
П1
П2

Вывод:
При замене плоскости проекций П2 на новую плоскость П4 положение новой прямоугольной проекции точки определяется ее аппликатой (координатой Z)
При замене плоскости проекций П1 на новую плоскость П5 положение новой прямоугольной проекции точки определяется ее ординатой (координатой Y)

Метрическая задача
Определить натуральную величину
треугольника АВС и угол его наклона к горизонтальной плоскости проекций
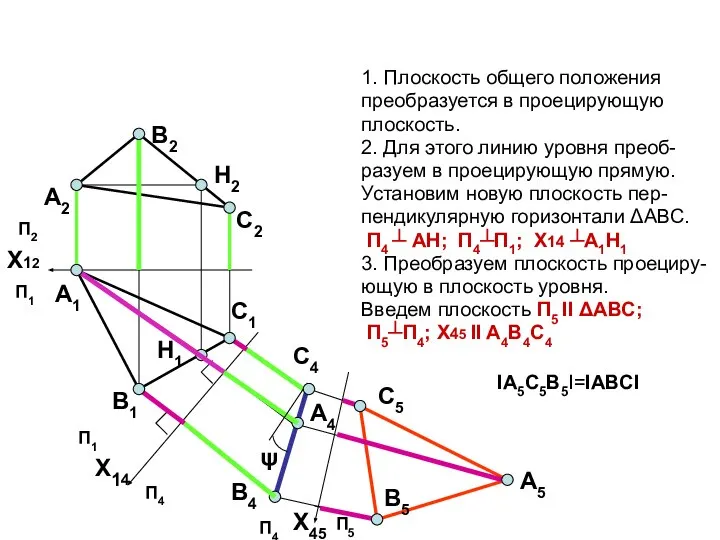
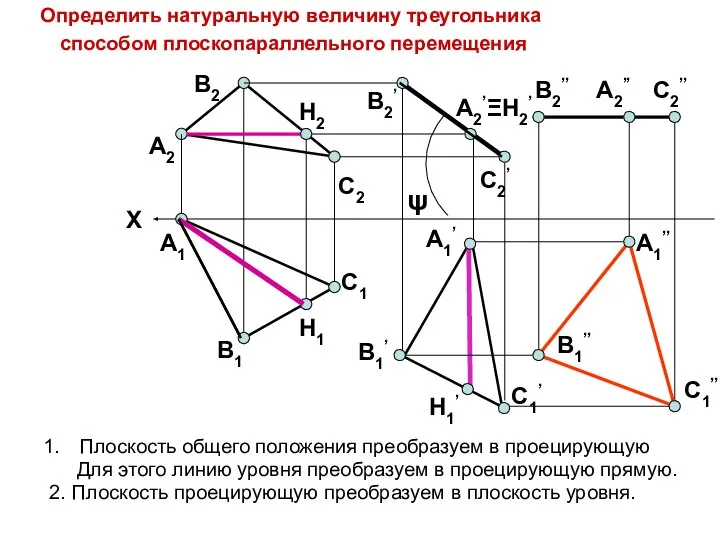
А(90,0,20); В(60,50,40); С(10,20,10)

1. Плоскость общего положения
преобразуется в проецирующую
плоскость.
2. Для этого линию уровня преоб-
разуем в проецирующую прямую.
Установим новую плоскость пер-
пендикулярную горизонтали ΔАВС.
П4 ┴ АH; П4┴П1; X14 ┴A1H1
3. Преобразуем плоскость проециру-
ющую в плоскость уровня.
Введем плоскость П5 ІІ ΔАВС;
П5┴П4; X45 II A4B4C4
X12
A1
B2
B1
C1
C2
A2
H2
H1
X14
A4
B4
C4
X45
В5
С5
А5
ІА5С5В5І=ІАВСІ
ψ
П1
П5
П4
П1
П2
П4

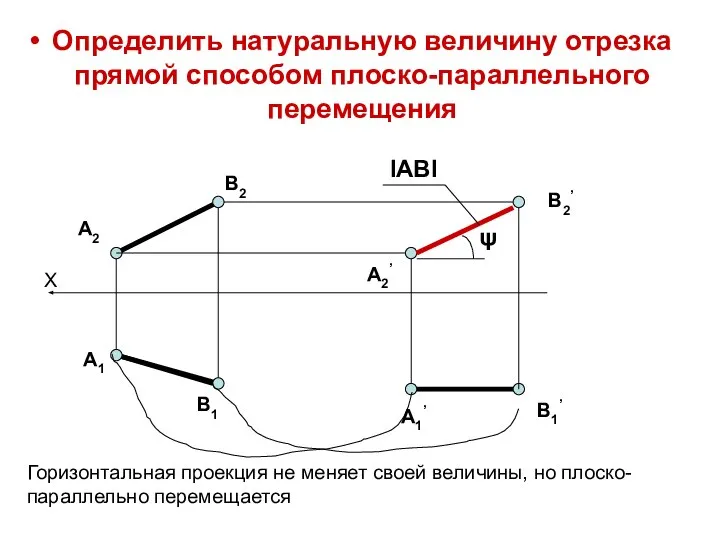
Сущность способа плоскопараллельного перемещения
Заданный геометрический объект совершает плоскопараллельное движение, при котором ВСЕ ЕГО ТОЧКИ движутся параллельно некоторой плоскости до положения параллельного или перпендикулярного плоскости проекций
Линия, по которой происходит перемещение всех точек объекта, находится В ПЛОСКОСТИ УРОВНЯ

Определить натуральную величину отрезка прямой способом плоско-параллельного перемещения
X
A2
B1
A1
B2
A1’
B1’
A2’
B2’
ψ
IАВI
Горизонтальная проекция не меняет своей величины, но плоско- параллельно перемещается

Плоскость общего положения преобразуем в проецирующую
Для этого линию уровня преобразуем в проецирующую прямую.
2. Плоскость проецирующую преобразуем в плоскость уровня.
Определить натуральную величину треугольника
способом плоскопараллельного перемещения
X
A1
B1
C1
C2
B2
A2
A1’
C1’
B1’
C2’
B2’
A2’ΞH2’
B2’’
A2’’
C2’’
B1’’
A1’’
C1’’
H1
H2
H1’
ψ

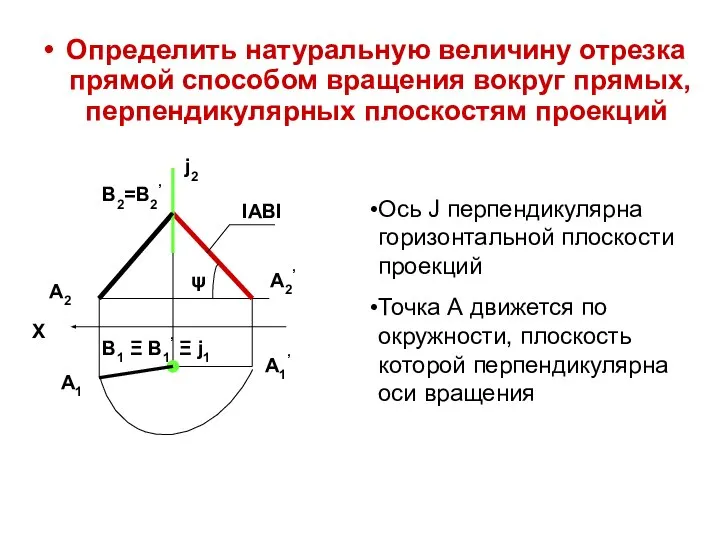
Сущность способа вращения вокруг прямых, перпендикулярных плоскостям проекций
Заданный геометрический объект вращается вокруг оси до положения параллельного или перпендикулярного какой-либо плоскости проекций.
Все точки объекта движутся по окружностям, которые располагаются в плоскостях уровня, перпендикулярных оси вращения.

Определить натуральную величину отрезка прямой способом вращения вокруг прямых, перпендикулярных плоскостям проекций
A2
B1 Ξ В1’ Ξ j1
A1
B2=В2’
j2
X
A1’
A2’
IABI
Ось J перпендикулярна горизонтальной плоскости проекций
Точка А движется по окружности, плоскость которой перпендикулярна оси вращения
ψ

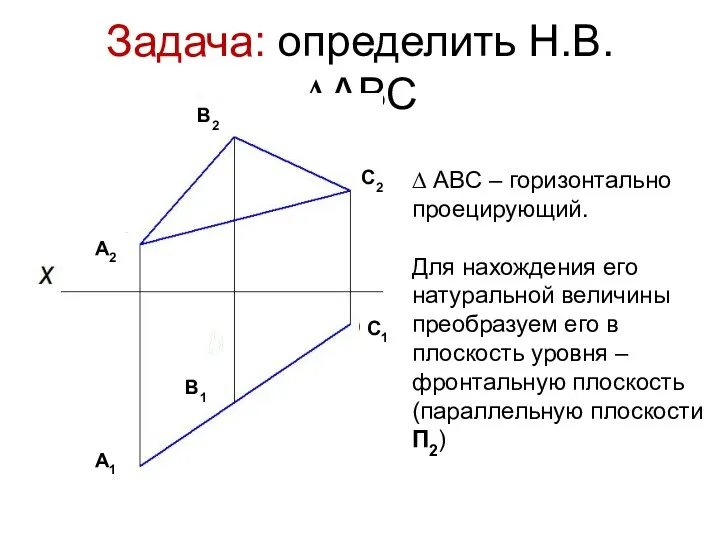
Задача: определить Н.В. ∆АВС
∆ АВС – горизонтально проецирующий.
Для нахождения его натуральной величины преобразуем его в плоскость уровня – фронтальную плоскость (параллельную плоскости П2)
A1
B1
C1
A2
B2
C2

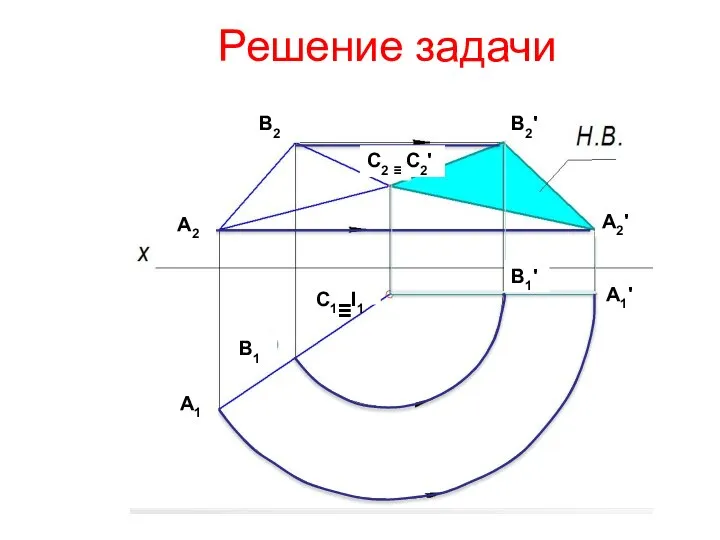
Решение задачи
A1
C1≡I1
B1
B1'
A1'
A2'
B2'
C2 ≡ C2'
B2
A2