Содержание
- 2. Лекція1«ШАМАНСТВО» В АНАЛіЗі ДАНИХ Інтелектуальний аналіз даних © ЄА. Лавров, 2015-2019 /14
- 3. Теоретико-системные основы математического моделирования (с) Н.М. Светлов, 2006 /20 План 1. Передмова 2. Управління силою думки
- 4. Теоретико-системные основы математического моделирования (с) Н.М. Светлов, 2006 /20 1. Передмова Іноді помітити феномен набагато цінніше,
- 5. Теоретико-системные основы математического моделирования (с) Н.М. Светлов, 2006 /20 2. Управління силою думки Не постачайте дітей
- 6. Теоретико-системные основы математического моделирования (с) Н.М. Светлов, 2006 /20 Людина сідає перед комп'ютером, а йому на
- 7. Теоретико-системные основы математического моделирования (с) Н.М. Светлов, 2006 /20 Рис. 1. Гра в теніс за комп'ютером
- 8. Теоретико-системные основы математического моделирования (с) Н.М. Светлов, 2006 /20 Є спеціальні системи введення слів за допомогою
- 9. Теоретико-системные основы математического моделирования (с) Н.М. Светлов, 2006 /20 Є спеціальні інвалідні крісла, які приводяться в
- 10. Теоретико-системные основы математического моделирования (с) Н.М. Светлов, 2006 /20 Мова йде не про розуміння думок людини
- 11. Теоретико-системные основы математического моделирования (с) Н.М. Светлов, 2006 /20 По тематиці «Brain Computer Interface» було проведено
- 12. Теоретико-системные основы математического моделирования (с) Н.М. Светлов, 2006 /20 Рішення описаної задачі Всі ілюстрації, які у
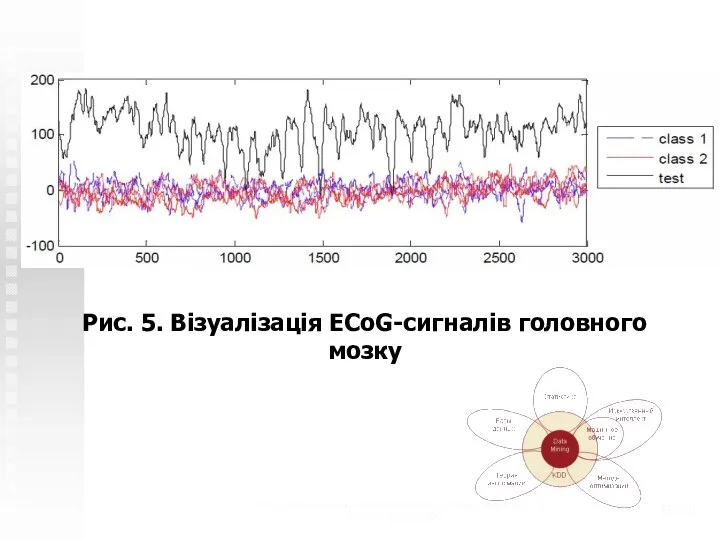
- 13. Теоретико-системные основы математического моделирования (с) Н.М. Светлов, 2006 /20 Рис. 5. Візуалізація ECoG-сигналів головного мозку
- 14. Теоретико-системные основы математического моделирования (с) Н.М. Светлов, 2006 /20 Найприродніший метод класифікації - подивитися, на сигнали
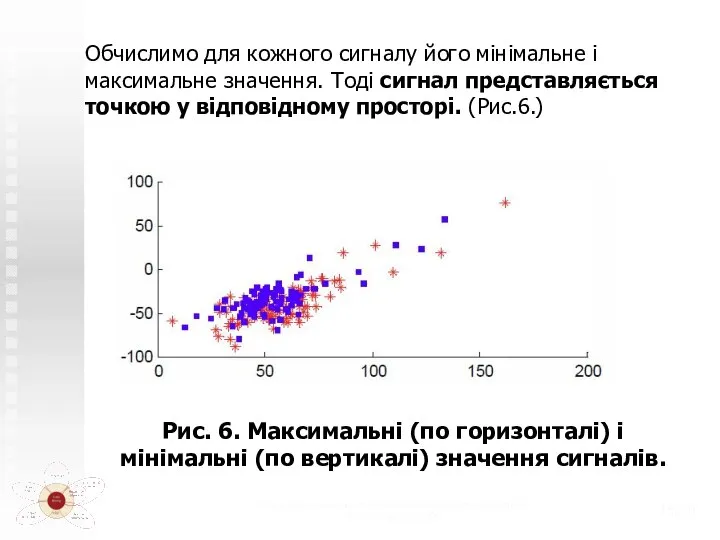
- 15. Теоретико-системные основы математического моделирования (с) Н.М. Светлов, 2006 /20 Обчислимо для кожного сигналу його мінімальне і
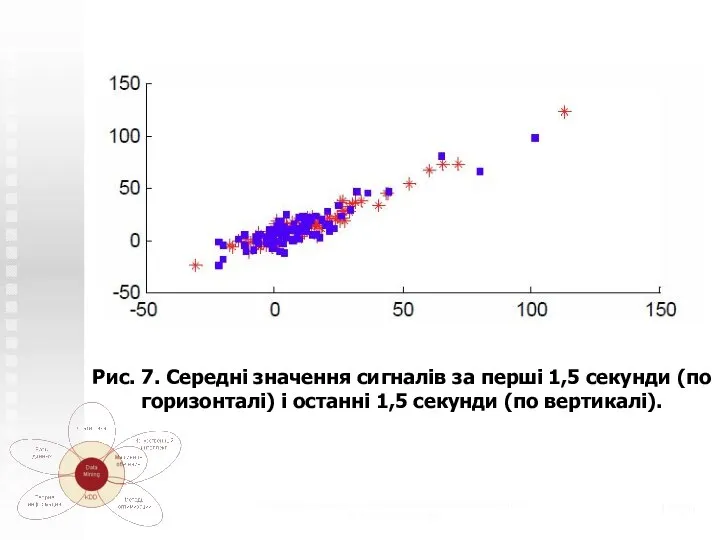
- 16. Теоретико-системные основы математического моделирования (с) Н.М. Светлов, 2006 /20 Ще приклад такого простору (рис. 7). Тут
- 17. Теоретико-системные основы математического моделирования (с) Н.М. Светлов, 2006 /20 Рис. 7. Середні значення сигналів за перші
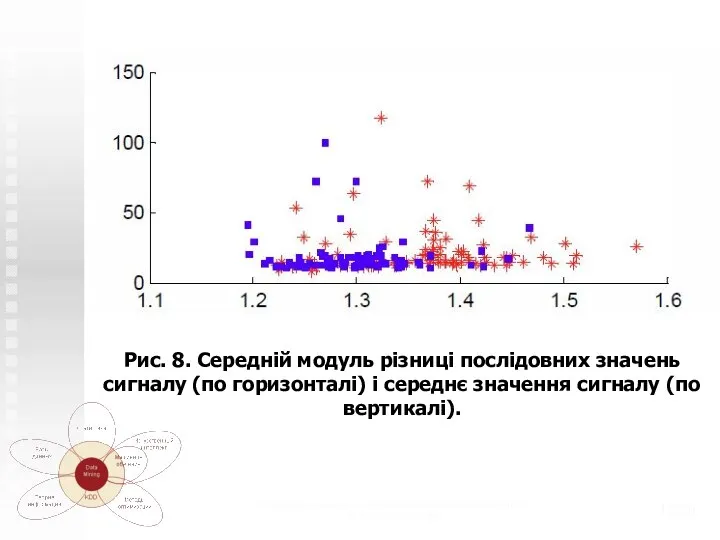
- 18. Теоретико-системные основы математического моделирования (с) Н.М. Светлов, 2006 /20 На (рис.8.) По вертикалі відкладено середнє значення
- 19. Теоретико-системные основы математического моделирования (с) Н.М. Светлов, 2006 /20 Рис. 8. Середній модуль різниці послідовних значень
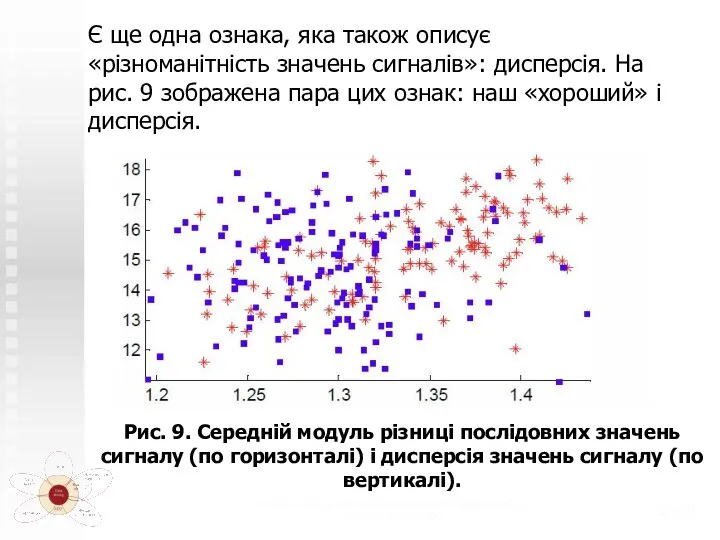
- 20. Теоретико-системные основы математического моделирования (с) Н.М. Светлов, 2006 /20 Є ще одна ознака, яка також описує
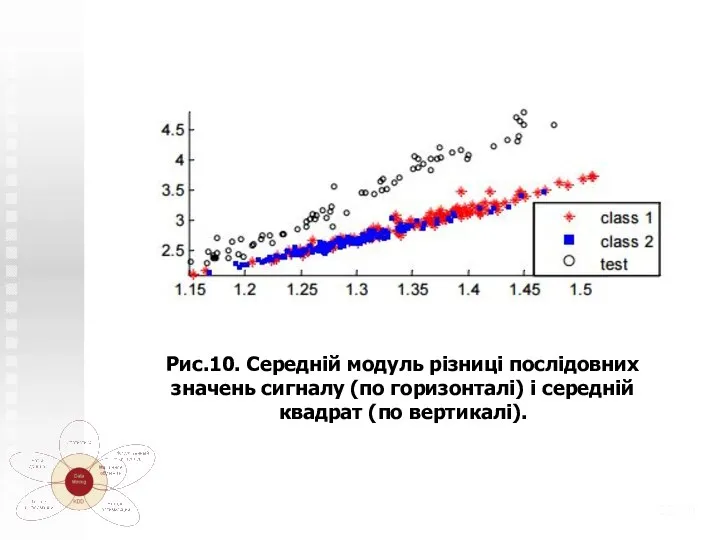
- 21. Ще один стандартний прийом, застосовуваний при візуальному аналізі даних: «трохи» змінити знайдену ознаку. Замість модуля використовувати
- 22. /20 Рис.10. Середній модуль різниці послідовних значень сигналу (по горизонталі) і середній квадрат (по вертикалі).
- 23. Отже, ми, власне, вирішили задачу! Звичайно, не з 100% -й точністю (яка тут і не досяжна),
- 24. 3. Дивовижні закономірності Не обтяжувати дітей мертвим вантажем фактів, навчіть їх прийомам і способам, які допоможуть
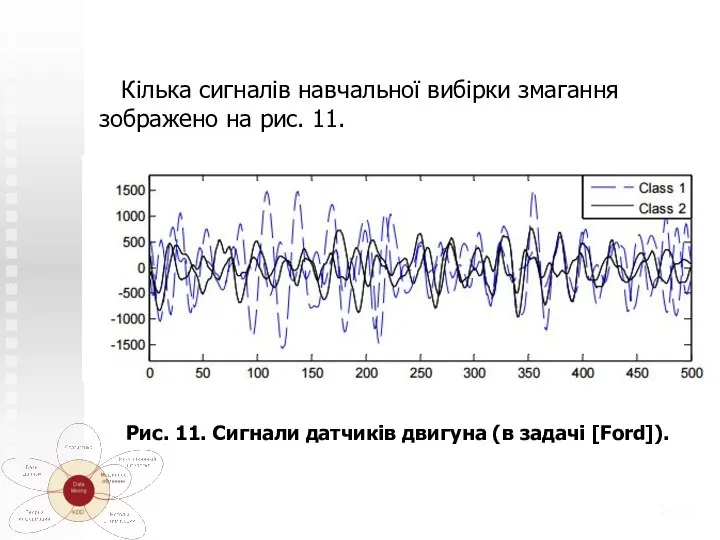
- 25. Постановка На міжнародному змаганні «Ford Classification Challenge» 2008 [Ford] треба було розробити алгоритм, який розрізняє сигнали
- 26. Кілька сигналів навчальної вибірки змагання зображено на рис. 11. Рис. 11. Сигнали датчиків двигуна (в задачі
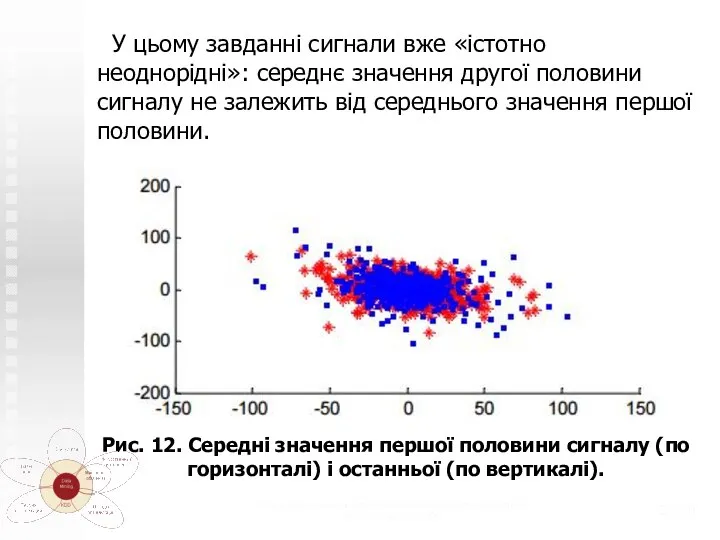
- 27. У цьому завданні сигнали вже «істотно неоднорідні»: середнє значення другої половини сигналу не залежить від середнього
- 28. У цьому завданні сигнали вже «істотно неоднорідні»: середнє значення другої половини сигналу не залежить від середнього
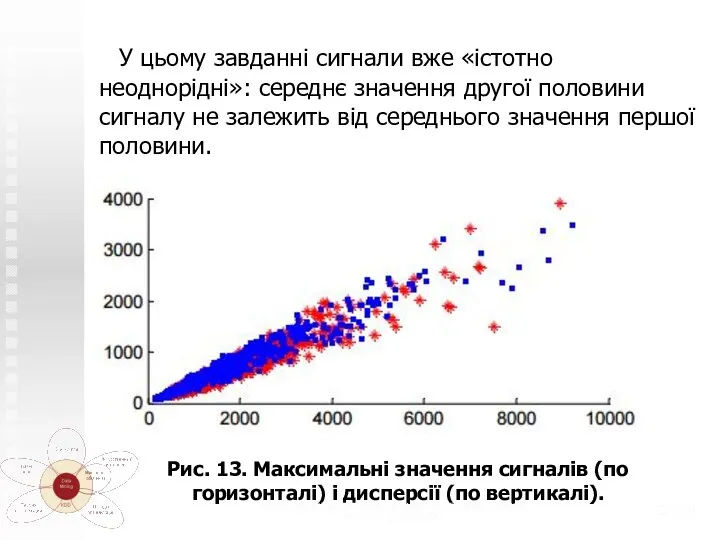
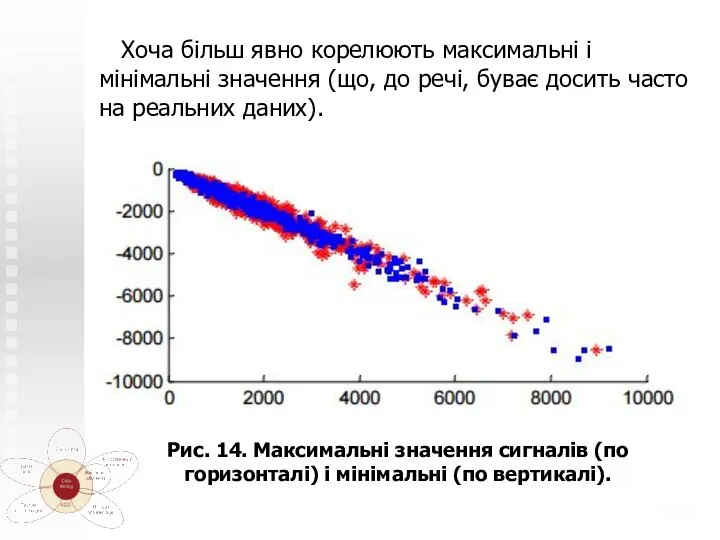
- 29. Хоча більш явно корелюють максимальні і мінімальні значення (що, до речі, буває досить часто на реальних
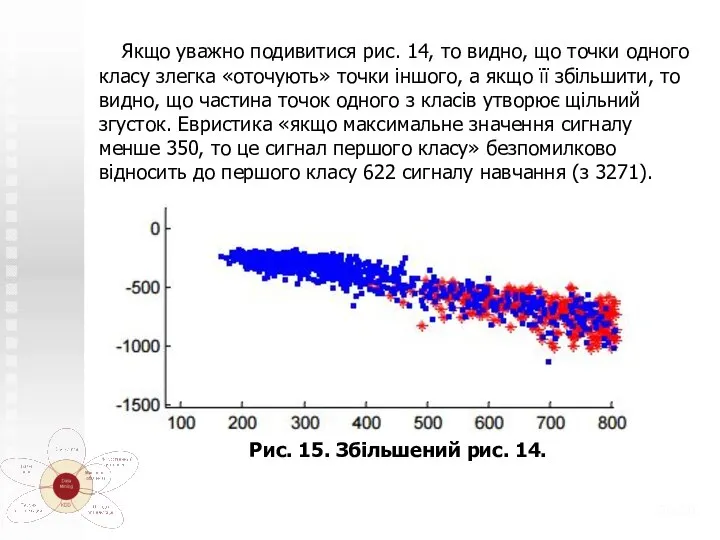
- 30. Якщо уважно подивитися рис. 14, то видно, що точки одного класу злегка «оточують» точки іншого, а
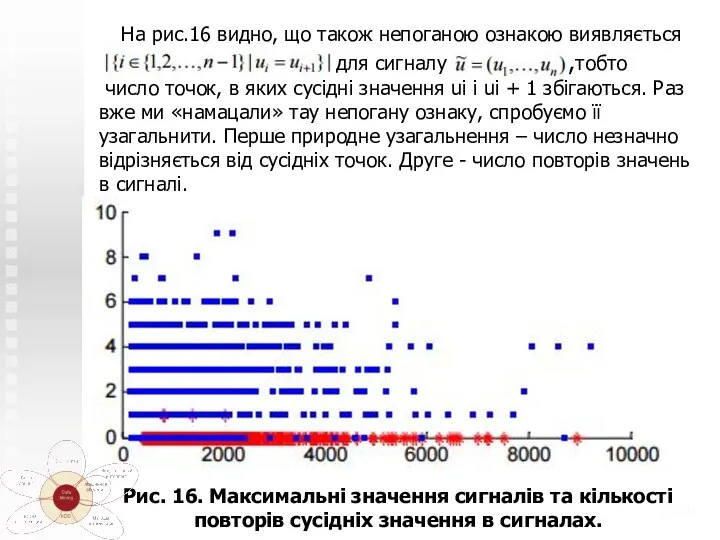
- 31. На рис.16 видно, що також непоганою ознакою виявляється для сигналу ,тобто число точок, в яких сусідні
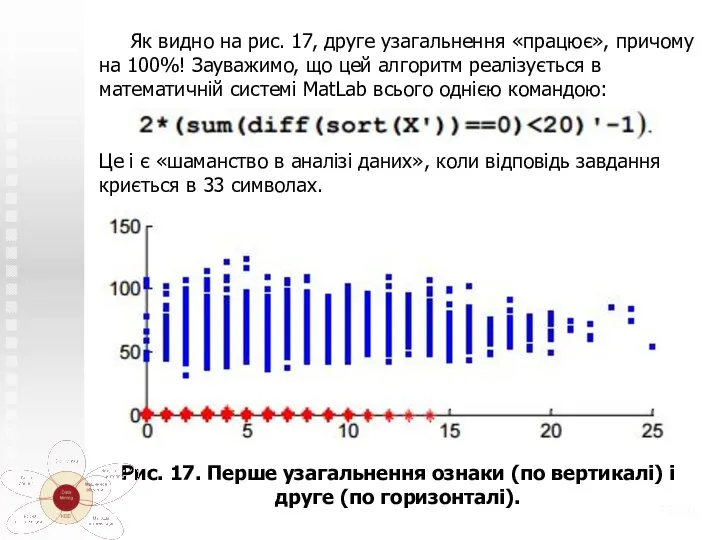
- 32. Як видно на рис. 17, друге узагальнення «працює», причому на 100%! Зауважимо, що цей алгоритм реалізується
- 33. 4. Правила справжнього шамана Дорога до істини вміщено парадоксами (О. Уайльд) Спочатку треба «подивитися на задачу».
- 34. Час не щадить те, що зроблено без витрати часу. (Е. Делакруа) 3. Рішення прикладних задач вимагає
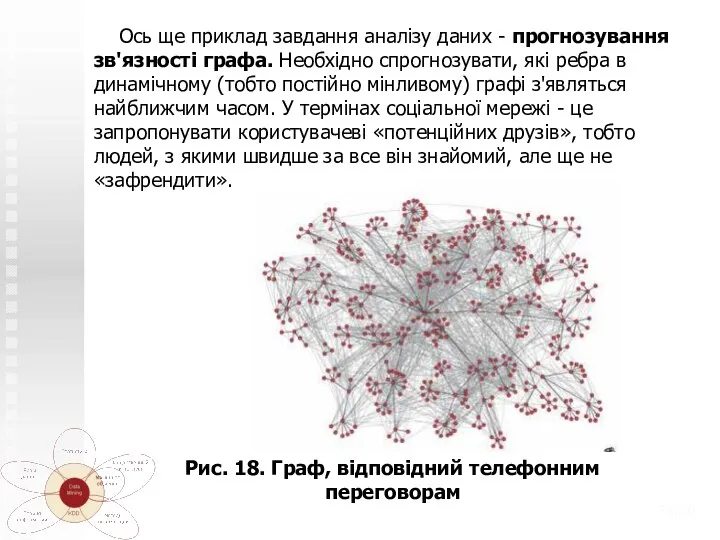
- 35. Ось ще приклад завдання аналізу даних - прогнозування зв'язності графа. Необхідно спрогнозувати, які ребра в динамічному
- 36. З погляду програмування дуже схожі зовсім різні завдання. Задача ієрархічної класифікації текстів. Є новинний ресурс, всі
- 38. Скачать презентацию














![Постановка На міжнародному змаганні «Ford Classification Challenge» 2008 [Ford] треба було розробити](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/989217/slide-24.jpg)



 Tekhnologii_ERP
Tekhnologii_ERP Платформа Freescale Semiconductor для реализации беспроводных решений ZigBee / 802.15.4 / SMAC
Платформа Freescale Semiconductor для реализации беспроводных решений ZigBee / 802.15.4 / SMAC Системы телемедицины. Программное обеспечение для телемедицины. Лекция 4
Системы телемедицины. Программное обеспечение для телемедицины. Лекция 4 Основы программирования на языке C++
Основы программирования на языке C++ Какво представлява WebAssembly
Какво представлява WebAssembly Введення повідомлення 05 про склад поїзда
Введення повідомлення 05 про склад поїзда лекция 5
лекция 5 Сэмюэл Морзе – телеграф и код Морзе
Сэмюэл Морзе – телеграф и код Морзе Информация, сообщения
Информация, сообщения Programing C
Programing C Задача о потоке минимальной стоимости
Задача о потоке минимальной стоимости Программирование циклов
Программирование циклов Презентация на тему Электронные деньги
Презентация на тему Электронные деньги  Коммерческое предложение по составлению SEO-стратегии
Коммерческое предложение по составлению SEO-стратегии Система управления базами данных моделирование и формализация. 9 класс
Система управления базами данных моделирование и формализация. 9 класс Концепция развития сервисного обслуживания предприятий Машиностроительного комплекса
Концепция развития сервисного обслуживания предприятий Машиностроительного комплекса ЭБС Букап
ЭБС Букап Алгоритмы и исполнители. Основы алгоритмизации
Алгоритмы и исполнители. Основы алгоритмизации Формирование информационной грамотности через работу с текстом на уроках окружающего мира
Формирование информационной грамотности через работу с текстом на уроках окружающего мира Устройство анализа сетевого трафика ЦПС
Устройство анализа сетевого трафика ЦПС Просмотр и редактирование жесткого диска (DiskEditor)
Просмотр и редактирование жесткого диска (DiskEditor) Технологии мультимедиа и восприятие ощущений. Общая физиология зрения
Технологии мультимедиа и восприятие ощущений. Общая физиология зрения Использование социальных сетей в деятельности педагога
Использование социальных сетей в деятельности педагога Презентация на тему Создание WEB–сайта с помощью языка HTML
Презентация на тему Создание WEB–сайта с помощью языка HTML  Правила расположения рук на клавиатуре
Правила расположения рук на клавиатуре Вредоносные ПО
Вредоносные ПО Определение каскадной точки входа
Определение каскадной точки входа Связь между листами. Лабораторная работа
Связь между листами. Лабораторная работа