Содержание
- 2. ИСТОРИЯ Для чего были придуманы логарифмы? Конечно, для ускорения и упрощения вычислений. Изобретатель первых логарифмических таблиц,
- 3. ИСТОРИЯ Принцип, лежащий в основе любой системы логарифмов, известен очень давно и может быть прослежен в
- 4. ИСТОРИЯ Штифель заметил, что сумма двух чисел в первой строке (строке показателей степени) равна показателю степени
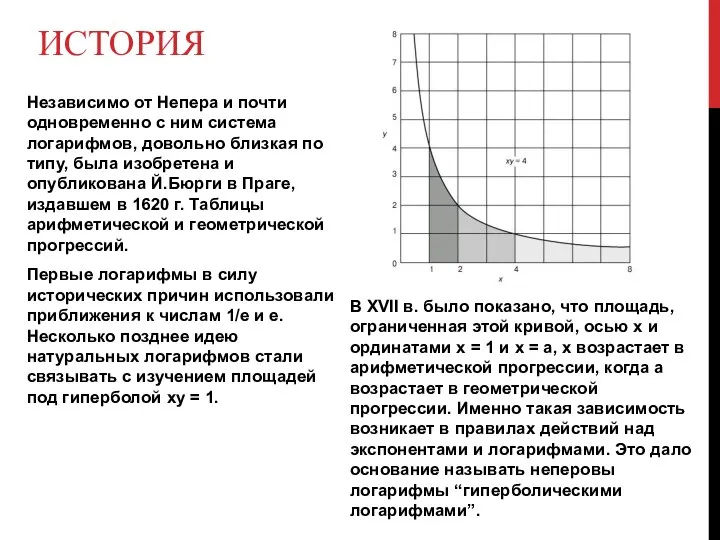
- 5. ИСТОРИЯ Независимо от Непера и почти одновременно с ним система логарифмов, довольно близкая по типу, была
- 6. ОПРЕДЕЛЕНИЕ Логарифм положительного числа b по основанию a — это показатель степени, в которую надо возвести
- 7. ЛОГАРИФМЫ Десятичный логарифм — логарифм с основанием 10, который обозначается как Натуральный логарифм — логарифм с
- 8. СВОЙСТВА ЛОГАРИФМОВ
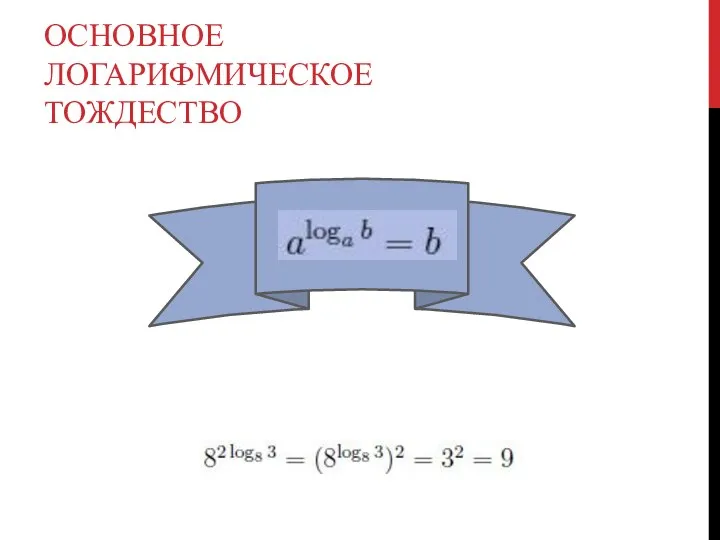
- 9. ОСНОВНОЕ ЛОГАРИФМИЧЕСКОЕ ТОЖДЕСТВО
- 10. Решенья их мне словно дети, Которых всей душой растишь. Пишу я с трепетом в ответе: Один
- 11. Логарифм произведения — это сумма логарифмов Логарифм частного — это разность логарифмов
- 12. СВОЙСТВА СТЕПЕНИ ЛОГАРИФМИРУЕМОГО ЧИСЛА И ОСНОВАНИЯ ЛОГАРИФМА Показатель степени логарифмируемого числа Показатель степени основания логарифма в
- 13. ПЕРЕХОД К НОВОМУ ОСНОВАНИЮ в частности, если c = b, то
- 15. Скачать презентацию










 Нашествие с Востока (1237-1240)
Нашествие с Востока (1237-1240) Презентация на тему Кино, кинематограф
Презентация на тему Кино, кинематограф  История Казахстана (1914 – до сегодня)
История Казахстана (1914 – до сегодня) Российское государство на рубеже столетий и правление Александра I
Российское государство на рубеже столетий и правление Александра I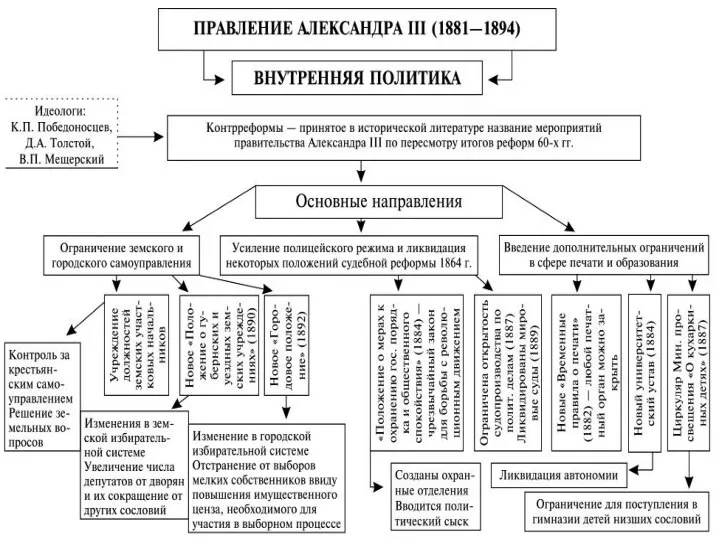 Правление Александра III
Правление Александра III Презентация на тему Общественное движение при Александре 2
Презентация на тему Общественное движение при Александре 2  Некрополи новгородских храмов как источник по изучению повседневной жизни древнерусского города
Некрополи новгородских храмов как источник по изучению повседневной жизни древнерусского города Народы Поволжья в XVI веке
Народы Поволжья в XVI веке Георгий Фёдорович Тимушев - герой Советского Союза
Георгий Фёдорович Тимушев - герой Советского Союза Империя Карла Великого и ее распад
Империя Карла Великого и ее распад Лента времени. Хронология (от греч. Χρόνος — время; λόγος — учение)
Лента времени. Хронология (от греч. Χρόνος — время; λόγος — учение) Феодализм на Руси
Феодализм на Руси Поездка в музей народного хора Ветеран
Поездка в музей народного хора Ветеран Презентация на тему Реформа политической системы: цели, этапы, итоги
Презентация на тему Реформа политической системы: цели, этапы, итоги  Образование очага войны на Дальнем Востоке. Дальневосточный узел международных противоречий
Образование очага войны на Дальнем Востоке. Дальневосточный узел международных противоречий Город-герой Тула
Город-герой Тула Великодный Василий Петрович. 1919 – 1982
Великодный Василий Петрович. 1919 – 1982 Искусство Чукотки
Искусство Чукотки Мужество Солдата. Посвящается памяти сержанта Крыгина С.Г
Мужество Солдата. Посвящается памяти сержанта Крыгина С.Г Распад СССР. Образование СНГ в 1991 году
Распад СССР. Образование СНГ в 1991 году Демократия в Древней Греции
Демократия в Древней Греции Омск в годы Великой Отечественной войны
Омск в годы Великой Отечественной войны Презентация на тему Троянская война в поэме Гомера "Илиада"
Презентация на тему Троянская война в поэме Гомера "Илиада"  Столица Казанского ханства
Столица Казанского ханства Состав скоплений охры из Каповой пещеры
Состав скоплений охры из Каповой пещеры Годы, опалённые войной Локнянский район в годы оккупации 22 июля 1941г.- 26 февраля 1944г.
Годы, опалённые войной Локнянский район в годы оккупации 22 июля 1941г.- 26 февраля 1944г. Внешняя политика Александра I в 1801-1812 г.г
Внешняя политика Александра I в 1801-1812 г.г История российской культуры с Анастасией Манохиной. Культура древней Руси X - начала XII века
История российской культуры с Анастасией Манохиной. Культура древней Руси X - начала XII века