Содержание
- 2. Триглиф (греч. triglyphos, от tri-, в сложных словах - три и glypho - режу), прямоугольная, несколько
- 3. На каждый интерколумний приходилось (в эпоху расцвету) по 2 метопы и 2 триглифа. Последние располагались над
- 4. Для того чтобы триглифный фриз получил на углах периптера (портика и т. д.) метрически четкое и
- 5. Между тем в реальных постройках триглифы, как правило, были уже поперечного сечения архитрава, и это неизбежно
- 6. Несложные вычисления, впервые произведенные Кольдевеем, показывают, что если ширина поперечного сечения архитрава А больше ширины триглифа
- 7. Такое композиционное решение углов в храмах и других ордерных постройках может считаться типичным для зрелой формы
- 9. Скачать презентацию
Слайд 2Триглиф (греч. triglyphos, от tri-, в сложных словах - три и glypho
Триглиф (греч. triglyphos, от tri-, в сложных словах - три и glypho

Слайд 3На каждый интерколумний приходилось (в эпоху расцвету) по 2 метопы и 2
На каждый интерколумний приходилось (в эпоху расцвету) по 2 метопы и 2

Слайд 4Для того чтобы триглифный фриз получил на углах периптера (портика и т.
Для того чтобы триглифный фриз получил на углах периптера (портика и т.

Размещение углового триглифа (разные варианты): а — ширина архитрава балки; т — ширина триглифа; м — ширина метопы; Иу— интерколумний угловой; Ин — интерколумний нормальный
Слайд 5Между тем в реальных постройках триглифы, как правило, были уже поперечного сечения
Между тем в реальных постройках триглифы, как правило, были уже поперечного сечения

Слайд 6Несложные вычисления, впервые произведенные Кольдевеем, показывают, что если ширина поперечного сечения архитрава
Несложные вычисления, впервые произведенные Кольдевеем, показывают, что если ширина поперечного сечения архитрава

Размещение углового триглифа (разные варианты): а — ширина архитрава балки; т — ширина триглифа; м — ширина метопы; Иу— интерколумний угловой; Ин — интерколумний нормальный
Слайд 7Такое композиционное решение углов в храмах и других ордерных постройках может считаться
Такое композиционное решение углов в храмах и других ордерных постройках может считаться

В храме Аполлона в Коринфе угловые пролеты сужены на торцовых фасадах до 3,77 м, на продольных— 3,48 м. Это сужение, нацеленное на решение проблемы углового триглифа, недостаточно значительно. Для более или менее незаметного для зрителя выравнивания частей фриза крайние к углу метопы были уширены примерно на 5 см.
Коринф. Храм Аполлона. фасад (реконструкция)
 Путешествие в Древнюю Русь
Путешествие в Древнюю Русь Екатерина Великая
Екатерина Великая Мой 20 век
Мой 20 век Отечественная война 1812 года
Отечественная война 1812 года 7 подвигов Александра Невского
7 подвигов Александра Невского Презентация на тему "Византийское тысячелетие (395-1453)" - презентации по Истории
Презентация на тему "Византийское тысячелетие (395-1453)" - презентации по Истории  Геноцид
Геноцид История славянской азбуки
История славянской азбуки История одной песни. Синий платочек
История одной песни. Синий платочек Тучково в годы Великой Отечественной войны
Тучково в годы Великой Отечественной войны Великая Отечественная война в истории моей семьи. Я горжусь своими прадедами
Великая Отечественная война в истории моей семьи. Я горжусь своими прадедами Классный час. Помнят люди
Классный час. Помнят люди Социально-экономическое развитие страны в первой четверти XIX в
Социально-экономическое развитие страны в первой четверти XIX в Стоунхендж /Stonehenge
Стоунхендж /Stonehenge Православие в Древней Руси (5 класс)
Православие в Древней Руси (5 класс) Россия - Родина моя
Россия - Родина моя Большевики и старообрядцы
Большевики и старообрядцы Карл Генрих Маркс Манифест коммунистической партии
Карл Генрих Маркс Манифест коммунистической партии Первые князья
Первые князья Варварская бомбардировка Сталинграда
Варварская бомбардировка Сталинграда Китай во второй половине XX века
Китай во второй половине XX века День энергетика
День энергетика Душегубец. История архаизма
Душегубец. История архаизма Ғұндар айналысқан шаруашылық түрлері
Ғұндар айналысқан шаруашылық түрлері Презентация на тему Виды рынков. Конкуренция и монополия
Презентация на тему Виды рынков. Конкуренция и монополия  Сформирование: в середине первого тысячелетия до нашей эры в северной части Индии
Сформирование: в середине первого тысячелетия до нашей эры в северной части Индии 15 февраля 1989 года - День вывода советских войск из Афганистана
15 февраля 1989 года - День вывода советских войск из Афганистана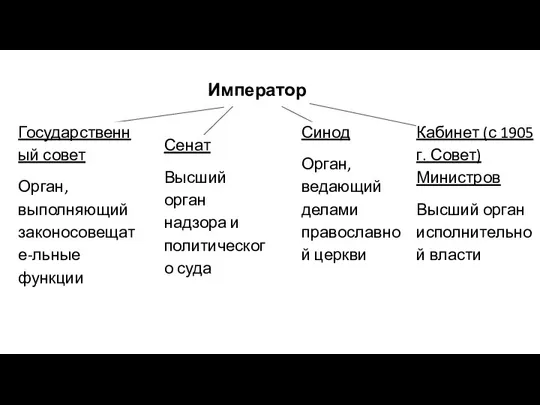 Представления населения о власти. Россия в начале ХХ века
Представления населения о власти. Россия в начале ХХ века