Слайд 3Содержание
Свойства фракталов
Классификация фракталов
Геометрические фракталы
Снежинка Коха и её построение
Треугольник и ковёр Серпинского
Пыль Кантора

и её построение
Кривые Пеано и их построение
Кривая Леви и её построение
Дерево Пифагора и его построение
Слайд 4Содержание
Алгебраические фракталы
Множества Жюлиа
Множество Мандельброта
Стохастические фракталы

Слайд 5Свойства фракталов
Фрактал (от лат. «Fractus» — «фрагментированный, изломанный, неправильный по форме») —

структура, состоящая из частей, которые в некотором смысле подобны целому.
Свойства:
Нерегулярность. Если фрактал описывать функцией, то свойство нерегулярности в математических терминах будет означать, что такая функция не дифференцируема, то есть не гладкая ни в какой точке.
Самоподобие означает, что у объекта нет характерного масштаба: будь у него такой масштаб, вы сразу бы отличили увеличенную копию фрагмента от исходного снимка.
Слайд 6Свойства фракталов
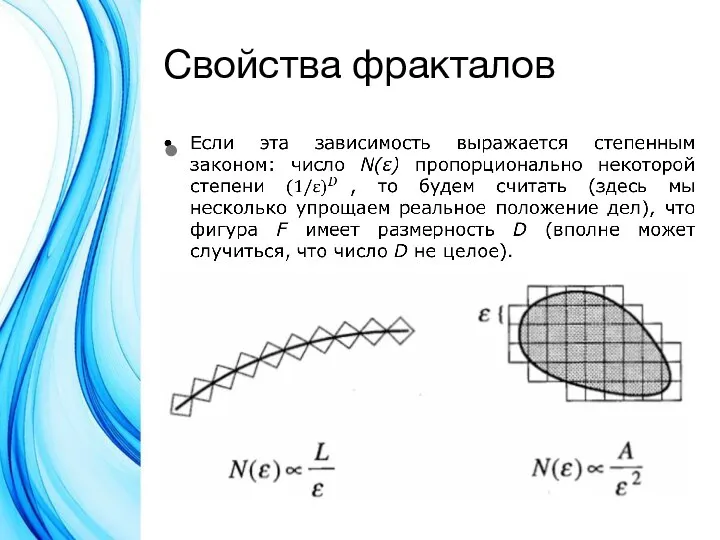
Размерность. Интуитивно мы понимаем термин размерность как число координат, необходимых для

задания положения точки внутри фигуры. Но фрактальные объекты имеют размерность, отличную от евклидовой. Фрактальная размерность является показателем сложности кривой.
Допустим, что фигура F, размерность которой мы хотим найти, расположена на плоскости. А плоскость, в свою очередь, покрыта сеткой из квадратиков со стороной ε. Через N(ε) обозначим число квадратиков, которые пересекаются с фигурой F (объединение всех таких квадратиков содержит в себе F). Ясно, что это число зависит от размера квадратиков: чем они меньше, тем больше их нужно, чтобы покрыть фигуру.
Слайд 8Классификация фракталов
Для представления многообразия фракталов удобно прибегнуть к их общепринятой классификации:
геометрические (конструктивные);
алгебраические
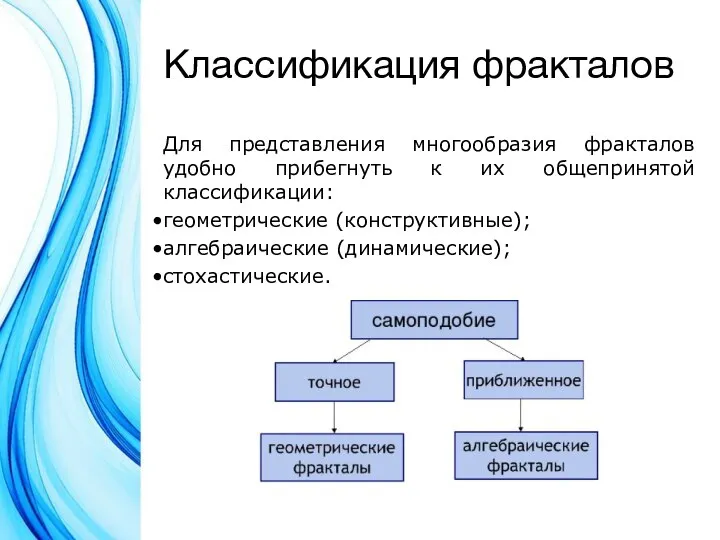
(динамические);
стохастические.
Слайд 9Геометрические фракталы
Это самый первый, ранний тип фракталов, с которых, по сути, и

началась история фракталов. Такие фракталы – одни из самых наглядных, в них сразу видно точное самоподобие частей при любых масштабах, и получаются они путём простых геометрических построений:
Задаётся фигура, на основе которой будет строиться фрактал.
К данной фигуре применяется набор правил, который преобразует её.
Бесконечно (или требуемое количество раз) повторяем применение набора правил.
Слайд 10Геометрические фракталы
Наиболее известными геометрическими фракталами являются снежинка Коха, ковёр и треугольник Серпинского,

пыль Кантора, кривые Пеано, кривая Леви, дерево Пифагора.
Слайд 11Снежинка Коха и её построение
Один из первых исследованных учёными фракталов.
Придумана шведским математиком

Хельге фон Кохом
в 1904 году.
Свойства:
Она непрерывна, но нигде не дифференцируема.
Имеет бесконечную длину.
Снежинка Коха ограничивает конечную площадь при бесконечном периметре.
Фрактальная размерность равна
log 4/log 3 = log34 ≈ 1,261859
Слайд 12Снежинка Коха и её построение
Начнём с равностороннего треугольника, который фактически является нулевой

итерации снежинки Коха.
Найдём центральную точку на каждом ребре текущей снежинки.
В центре каждого ребра добавим выступающий наружу равносторонний треугольник со стороной, равной 1/3 длины текущего ребра.
Определим следующую итерацию снежинки Коха, чтобы оказаться снаружи с внешней стороны предыдущей снежинки и всех добавленных треугольников.
Повторим шаги 2-4 необходимое количество раз.
Слайд 14Треугольник и ковёр Серпинского
Треугольник (салфетка) Серпинского был описан польским математиком Вацлавом Серпинским

в 1915 г.
Свойства:
Треугольник Серпинского имеет нулевую площадь.
Неожиданная связь с комбинаторикой. Если в треугольнике Паскаля с 2n строками покрасить все четные числа белым, а нечетные — черным, то видимые числа образуют треугольник Серпинского (в некотором приближении).
Квадратная версия фрактала была описана в 1916 году.
Слайд 15Треугольник и ковёр Серпинского
Чтобы получить треугольник Серпинского, нужно взять (равносторонний) треугольник с

внутренностью, провести в нём средние линии и выкинуть центральный из четырёх образовавшихся маленьких треугольников. Дальше эти же действия нужно повторить с каждым из оставшихся трёх треугольников,
и т. д.
Чтобы получить ковёр (квадрат) Серпинского, берётся квадрат, и также на каждом шаге выбрасывается центральная часть.
Слайд 17Пыль Кантора и её построение
Пыль (множество) Кантора — классический фрактал, описанный немецким

математиком Георгом Кантором в 1883 г.
Свойства:
Канторово множество замкнуто и не счётно.
Не содержит интервалов положительной длины.
Сумма длин интервалов, удалённых при построении множества С, в точности равна 1.
Пыль Кантора есть фрактал размерности
log 2/log 3 ≈ 0,6309.
Слайд 18Пыль Кантора и её построение
Построение классической пыли Кантора начинается с выбрасывания средней

трети (не включая концы) единичного отрезка.
То есть исходное множество есть отрезок [0,1], и первый шаг состоит в удалении открытого интервала (1/3,2/3). На следующем и всех остальных шагах мы выкидываем среднюю треть (не включая концы) всех отрезков текущего уровня.
Слайд 20Кривые Пеано и их построение
Кривые Пеано — общее название общее название для
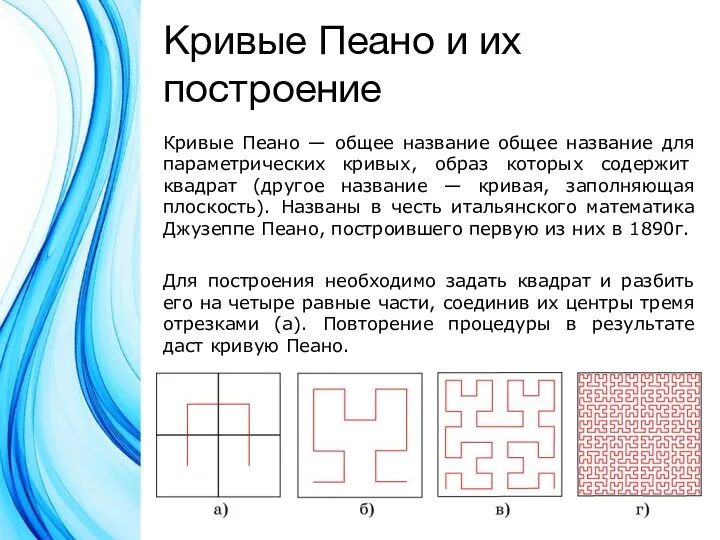
параметрических кривых, образ которых содержит квадрат (другое название — кривая, заполняющая плоскость). Названы в честь итальянского математика Джузеппе Пеано, построившего первую из них в 1890г.
Для построения необходимо задать квадрат и разбить его на четыре равные части, соединив их центры тремя отрезками (а). Повторение процедуры в результате даст кривую Пеано.
Слайд 22Кривая Леви и её построение
Хотя этот объект изучал еще итальянец Эрнесто Чезаро

в 1906 году, его самоподобие и фрактальные свойства исследовал в 1930-х годах француз Поль Пьер Леви. Фрактальная размерность границы этого фрактала примерно равна 1,9340... . Но это довольно сложный математический результат, а точное значение неизвестно.
За сходство с буквой «С», написанной витиеватым шрифтом, ее еще называют С-кривой Леви.
Слайд 23Дерево Пифагора и его построение
Пифагор, доказывая свою знаменитую теорему, построил фигуру, где

на сторонах прямоугольного треугольника расположены квадраты. В наш век эта фигура Пифагора выросла в целое дерево. Впервые дерево Пифагора построил А. Е. Босман (1891—1961) во время второй мировой войны, используя обычную чертёжную линейку.
Одним из свойств дерева Пифагора является то, что если площадь первого квадрата равна единице, то на каждом уровне сумма площадей квадратов тоже будет равна единице.
Слайд 24Дерево Пифагора и его построение
Если в классическом дереве Пифагора угол равен 45

градусам, то также можно построить и обобщённое дерево Пифагора при использовании других углов. Такое дерево часто называют обдуваемое ветром дерево Пифагора. Если изображать только отрезки, соединяющие каким-либо образом выбранные «центры» треугольников, то получается обнаженное дерево Пифагора.
Кроной дерева Пифагора является кривая Леви.
Слайд 25Дерево Пифагора и его построение

Слайд 26Алгебраические фракталы
Фракталы этого типа возникают при исследовании нелинейных динамических систем (отсюда и

название). Поведение такой системы можно описать комплексной нелинейной функцией (многочленом) f(z).
Возьмем какую-нибудь начальную точку z0 на комплексной плоскости. Теперь рассмотрим бесконечную последовательность чисел на комплексной плоскости, каждое следующее из которых получается из предыдущего:
z0, z1 = f(z0), z2 = f(z1), ... zn+1 = f(zn).
В зависимости от начальной точки z0 такая последовательность может вести себя по-разному: стремиться к бесконечности при n → ∞; сходиться к какой-то конечной точке; циклически принимать ряд фиксированных значений; возможны и более сложные варианты.
Слайд 27Алгебраические фракталы
Как известно (из синергетических представлений), нелинейные динамические системы могут иметь несколько

устойчивых состояний. При этом состояние, в котором оказалась динамическая система после определенного конечного числа итераций, напрямую зависит от ее начального состояния. А это значит, что изучаемая система может рассматриваться в некотором фазовом пространстве, в котором будут присутствовать области притяжения (аттракторы).
Рассматривая двумерное фазовое пространство и окрашивая области притяжения различными цветами, можно получить цветовой фазовый портрет любой системы. Применение различных алгоритмов выбора цвета позволяет получить достаточно сложные фрактальные картины с удивительными многоцветными узорами.
Слайд 28Алгебраические фракталы
Важным понятием в данной теме является понятие аттракторов — множеств, к
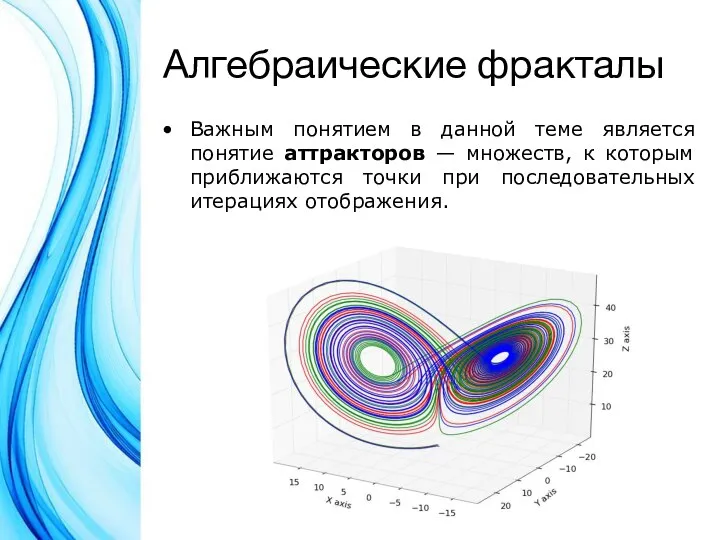
которым приближаются точки при последовательных итерациях отображения.
Слайд 29Множества Жюлиа
Любая точка z комплексной плоскости имеет свой характер поведения (остается конечной, стремится к

бесконечности, принимает фиксированные значения) при итерациях функции f(z), а вся плоскость делится на части. При этом точки, лежащие на границах этих частей, обладают таким свойством: при сколь угодно малом смещении характер их поведения резко меняется (такие точки называют точками бифуркации). При этом множества точек, имеющих один конкретный тип поведения, а также множества бифуркационных точек часто имеют фрактальные свойства. Это и есть множества Жюлиа для функции f(z).
Слайд 30Множества Жюлиа
Заполненное множество Жюлиа — множество точек, не стремящихся к бесконечности. Обычное

множество Жюлиа при этом является его границей.
Слайд 31Множество Мандельброта
Рассмотрим функцию fc(z) = z2 + с, где c —комплексное число. Построим последовательность этой функции с z0 = 0, в зависимости от

параметра с она может расходиться к бесконечности или оставаться ограниченной.
z0 = 0, z1 = z02 + с, ..., zn+1 = zn2 + c
При этом все значения с, при которых эта последовательность ограничена, как раз и образуют множество Мандельброта.
Слайд 32Множество Мандельброта
Визуально множество Мандельброта выглядит как набор бесконечного количества различных фигур, самая

большая из которых называется кардиоидой (она похожа на стилизованное изображение сердца и получила свое название от двух греческих слов — «сердце» и «вид»).
Кардиоида окружена всё уменьшающимися кругами, каждый из которых окружен еще меньшими кругами, и т. д. до бесконечности. При любом увеличении этого фрактала будут выявляться всё более и более мелкие детали изображения, дополнительные ветки с более мелкими кардиоидами, кругами.
Слайд 34Стохастические фракталы
Третьей крупной разновидностью фракталов являются стохастические фракталы, которые образуются путем многократных

повторений случайных изменений каких-либо параметров.
В результате итерационного процесса получаются объекты, очень похожие на природные фракталы — несимметричные деревья, изрезанные лагунами береговые линии островов и многое другое. Двумерные стохастические фракталы используются преимущественно при моделировании рельефа местности и поверхности моря.
Слайд 35Стохастические фракталы
Примеры стохастических фракталов:
траектория броуновского движения на плоскости и в пространстве;
различные виды

рандомизированных фракталов, то есть фракталов, полученных с помощью рекурсивной процедуры, в которую на каждом шаге введён случайный параметр.
Слайд 36Стохастические фракталы
Плазма — типичный представитель данного класса фракталов в компьютерной графике:
Для ее

построения возьмем прямоугольник и для каждого его угла определим цвет. Далее находим центральную точку прямоугольника и раскрашиваем ее в цвет равный среднему арифметическому цветов по углам прямоугольника плюс некоторое случайное число.
Слайд 37Стохастические фракталы
Ярким примером стохастических фракталов может служить броуновская поверхность, с помощью которой
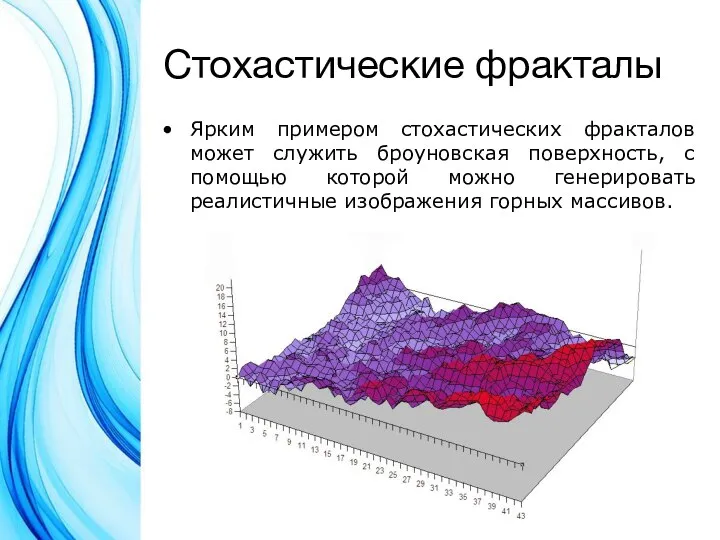
можно генерировать реалистичные изображения горных массивов.




































 Положительные и отрицательные числа (6 класс)
Положительные и отрицательные числа (6 класс) Задачи на построение
Задачи на построение Задачи линейный алгоритм
Задачи линейный алгоритм Методы решения тригонометрических уравнений
Методы решения тригонометрических уравнений Линии второго порядка
Линии второго порядка Отображение множеств. Диаграммы
Отображение множеств. Диаграммы Квадратный корень. Математический диктант
Квадратный корень. Математический диктант Десятичные и натуральные логарифмы
Десятичные и натуральные логарифмы Эконометрика. Временные ряды
Эконометрика. Временные ряды Решение уравнений третьей степени при подготовке к ЕГЭ
Решение уравнений третьей степени при подготовке к ЕГЭ Национальный стандарт по библиотечной статистике: преемственность и новые подходы
Национальный стандарт по библиотечной статистике: преемственность и новые подходы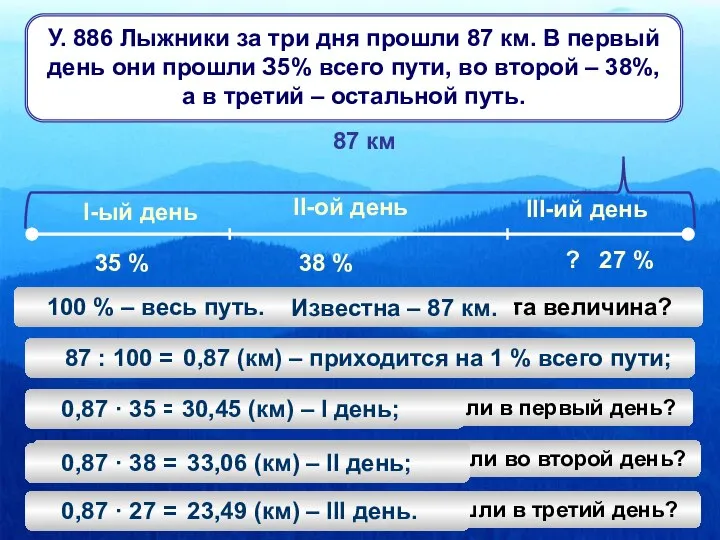 Задачи о лыжниках
Задачи о лыжниках Математический анализ
Математический анализ Четырёхугольники
Четырёхугольники Средние величины
Средние величины Проценты
Проценты Геометрия в искусстве
Геометрия в искусстве Использование метода ЛАЧХ для синтеза регуляторов манипулятора с гибким стержнем
Использование метода ЛАЧХ для синтеза регуляторов манипулятора с гибким стержнем Подобие треугольников
Подобие треугольников Возведение в квадрат суммы трех, четырех и более слагаемых
Возведение в квадрат суммы трех, четырех и более слагаемых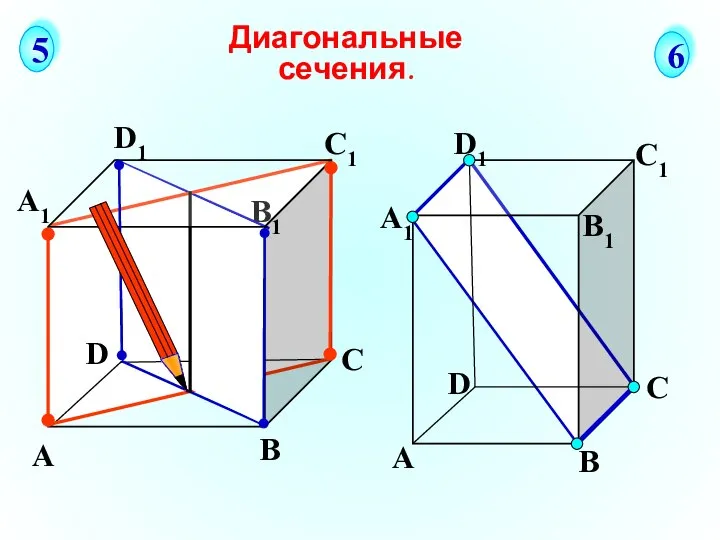 Диагональные сечения
Диагональные сечения Линейное уравнение с одной переменной
Линейное уравнение с одной переменной 38 попугаев
38 попугаев Ранг матрицы. Обратная матрица. Невырожденные матрицы
Ранг матрицы. Обратная матрица. Невырожденные матрицы Математический турнир Степень и ее свойства. 7 класс
Математический турнир Степень и ее свойства. 7 класс Презентация на тему Является ли система координат чисто математическим понятием
Презентация на тему Является ли система координат чисто математическим понятием  Статистика. Тренды
Статистика. Тренды ОГЭ 2020-21. Задание №9. Найдите корень уравнения
ОГЭ 2020-21. Задание №9. Найдите корень уравнения