MV1_Lektsia_2_-_Predstavlenie_nechetkikh_znaniy_-_kopia

Введение
Часто, представляя знания о сложных предметных областях, приходится сталкиваться с их неполнотой, неточностью, неоднозначностью, нечеткостью
Нечеткость связана с отсутствием точных границ области определений и свойственна большинству понятий
Эта нечеткость границ приводит к тому, что в общем случае оказывается невозможным решать вопрос о соответствии данного объекта и данного понятия по принципу да/нет
Часто можно только говорить о степени соотнесенности одного другому, оценивая ее, например, в интервале от 1 (определенное да) до 0 (определенное нет)
Это означает, что переход от полной принадлежности объекта классу к полной его непринадлежности происходит не скачком, а плавно, причем принадлежность объекта классу выражается числом из интервала [0,1]
Методы представления нечетких знаний были предложены американским профессором Л.Заде в 1965 году
Он ввел два фундаментальных понятия: лингвистическая переменная и нечеткое множество

Понятие лингвистической переменной (1)
Лингвистическая переменная (ЛП) – это переменная, значениями которой являются слова или выражения естественного (иногда искусственного) языка
Например, переменную Возраст можно рассматривать как лингвистическую переменную, если она принимает не числовые значения (например, от 0 до 100), а лингвистические значения, такие как молодой, старый, очень молодой, очень старый и т.п.
Лингвистическая переменная описывается кортежем:
(N, T(N), U, G, M), где
N – название лингвистической переменной
T(N) – терм-множество N, т.е. совокупность ее лингвистических значений
U – универсальное множество
G – синтаксическое правило, порождающее терм-множество T(N)
M – семантическое правило, которое каждому лингвистическому значению X ставит в соответствие его смысл M(X), причем M(X) обозначает нечеткое подмножество множества U (т.е. подмножество, границы которого размыты)

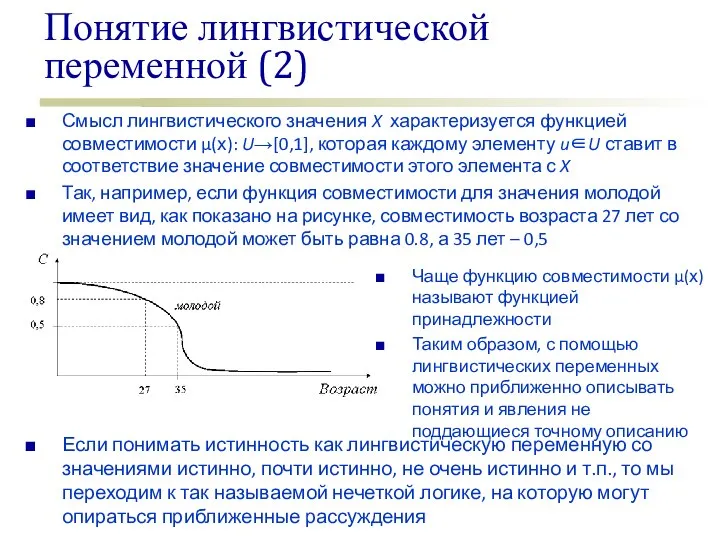
Понятие лингвистической переменной (2)
Смысл лингвистического значения X характеризуется функцией совместимости μ(х): U→[0,1], которая каждому элементу u∈U ставит в соответствие значение совместимости этого элемента с X
Так, например, если функция совместимости для значения молодой имеет вид, как показано на рисунке, совместимость возраста 27 лет со значением молодой может быть равна 0.8, а 35 лет – 0,5
Если понимать истинность как лингвистическую переменную со значениями истинно, почти истинно, не очень истинно и т.п., то мы переходим к так называемой нечеткой логике, на которую могут опираться приближенные рассуждения
Чаще функцию совместимости μ(х) называют функцией принадлежности
Таким образом, с помощью лингвистических переменных можно приближенно описывать понятия и явления не поддающиеся точному описанию

Нечеткие множества (1)
Нечеткое множество (НМ) A = {(x,μA(x))} определяется как совокупность упорядоченных пар, составленных из элементов x универсального множества X и соответствующих степеней принадлежности μA(x), или непосредственно в виде функции
μA: X →[0,1]
Универсальным множеством (УМ) X нечеткого множества A называется область определения функции принадлежности A
Носителем НМ A называется множество таких точек в X, для которых μA(x)>0
Высотой НМ A называется величина supμA(x)
Точкой перехода НМ A называется такой элемент множества X, степень принадлежности которого множеству A равна 0.5

Нечеткие множества (2)
Пример. Пусть УМ X представляет собой интервал [0,100], и переменная x, принимающая значения из этого интервала, интерпретируется как возраст
Нечеткое подмножество универсального множества X, обозначаемое термином старый, можно определить функцией принадлежности вида
μA(x) = 0, при 0 ≤x ≤50
μA(x) = (1+((x – 50)/5)-2)-1), при 50
В этом примере носителем НМ "старый" является интервал [50,100], высота близка к 1, а точкой перехода является значение x=55
Обычно НМ A универсального множества X записывается в виде
A = 1|x1 + 2|x2 + ... + n|xn
где i, i=1,...,n - степень принадлежности элемента xi НМ A

Нечеткие множества: основные операции (1)

Нечеткие множества: основные операции (2)

Нечеткие множества: нечеткие отношения (1)

Нечеткие множества: нечеткие отношения (2)
Пусть U = U1 × U2 × ... × Un — прямое произведение универ­сальных множеств и М — некоторое множество принадлежностей (например, М = [0, 1])
Нечеткое n-ое отношение определя­ется как нечеткое подмножество R на U, принимающее свои значения в М
В случае n= 2 и М = [0, 1] нечетким отношением R между множествами X = U1 и Y = U2 будет называться функ­ция
R:(X, Y) → [0, 1], которая ставит в соответствие каждой паре элементов (x, у) ϵ X × Y величину μR(x, у) ϵ [0, 1]
Обозначение: нечеткое отношение на X × Y запишется в виде
х ϵ X, у ϵ Y: xRy
В случае, когда X = У, т.е. X и Y совпадают, нечеткое отно­шение
R: X × X → [0, 1] называется нечетким отношением на множестве X

Нечеткие множества: нечеткие отношения: операции над нечеткими отношениями (1)

Нечеткие продукции: определение
Определение. В общем случае под правилом нечеткой продукции или просто — нечеткой продукцией понимается выражение следующего вида:
(i): Q;P; А⇒В ; S,F,N, где
( i )— имя нечеткой продукции
Q— сфера применения нечеткой продукции
Р— условие применимости ядра нечеткой продукции
А⇒В— ядро нечеткой продукции, в котором
А— условие ядра (или антецедент)
В— заключение ядра (или консеквент)
'⇒' — знак логической секвенции (или следования)
S — метод или способ определения количественного значения степени истинности заключения ядра
F— коэффициент определенности или уверенности нечеткой продукции
N— постусловия продукции
Аналогично классическим правилам продукций ядро А⇒В также является центральным компонентом нечеткой продукции

Нечеткие продукции: ядро продукции
Ядро продукции записывается в более привычной форме:
"ЕСЛИ А, ТО В"
или в наиболее распространенном виде:
"IF А, THEN В", где
А и В — некоторые выражения нечеткой логики, которые наиболее часто представляются в форме нечетких высказываний
При этом секвенция (⇒, ТО, THEN ) интерпретируется в обычном логическом смысле как знак логического следования заключения из условия
В качестве выражений и могут использоваться составные логические нечеткие высказывания, т. е. элементарные нечеткие высказывания (атомарные формулы), соединенные нечеткими логические связками, такими как:
нечеткое отрицание
нечеткая конъюнкция
нечеткая дизъюнкция

Нечеткие продукции: база знаний
Продукционная нечеткая система или система нечетких правил продукций представляет собой некоторое согласованное множество отдельных нечетких продукций или правил нечетких продукций в форме
"ЕСЛИ , ТО"
или в виде: "IF , THEN ", как определено в Стандарте
IEC 1131-7
Далее обе эти формы записи будут использоваться как эквивалентные в зависимости от удобства в том или ином контексте
Согласованное множество нечетких продукций также называется нечеткой базой знаний или базой нечетких продукций или базой нечетких правил

Нечеткие продукции: ядро продукции: посылки (1)
В правиле "ЕСЛИ А, ТО В" после ключевого слова "ЕСЛИ" следует антецедент (посылки) или по-другому условие правила – А
Посылки или условие правила зачастую состоит из подусловий – элементарных высказываний (атомарных формул)
А = {Аi| i=1, …,n, n – количество входных переменных}
Подусловие или атомарная формула имеет вид
<параметр> = <значение>, где
Параметр – это входная лингвистическая переменная хi∈Х
Значение – это терм t ∈T
Т – множество значений лингвистической переменной хi, его также называют базовым терм-множеством
Часто вместо знака равенства используют слово "есть", например,
"ЕСЛИ температура есть высокая И головная боль есть высокая ТО …"

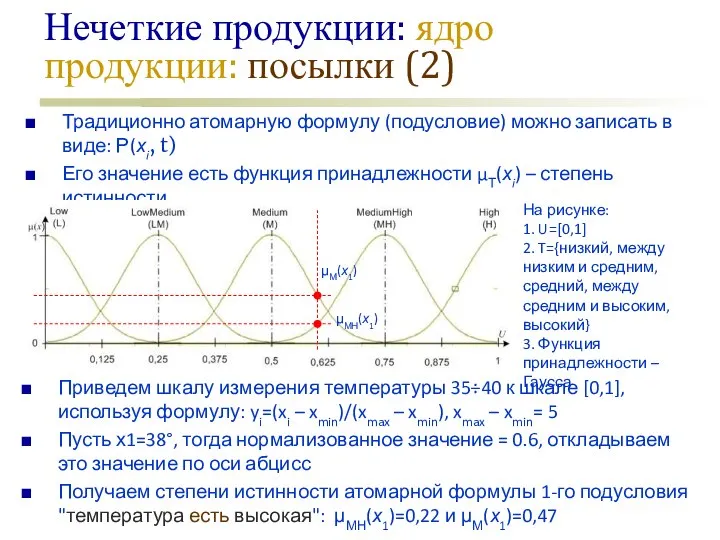
Нечеткие продукции: ядро продукции: посылки (2)
Традиционно атомарную формулу (подусловие) можно записать в виде: Р(хi, t)
Его значение есть функция принадлежности μТ(хi) – степень истинности
На рисунке:
1. U=[0,1]
2. T={низкий, между низким и средним, средний, между средним и высоким, высокий}
3. Функция принадлежности – Гаусса
Приведем шкалу измерения температуры 35÷40 к шкале [0,1], используя формулу: yi=(xi – xmin)/(xmax – xmin), xmax – xmin= 5
Пусть х1=38°, тогда нормализованное значение = 0.6, откладываем это значение по оси абцисс
Получаем степени истинности атомарной формулы 1-го подусловия "температура есть высокая": μМН(х1)=0,22 и μМ(х1)=0,47

Нечеткие продукции: ядро продукции: заключение правила(2)
В ядре продукции "ЕСЛИ А, ТО В" заключением правила (консеквентом) является элемент В
Заключение правила В также как и условие А может состоять из набора подзаключений
За исключением модели Сугено каждое подзаключение имеет такой же как и подусловие:
<параметр> = <значение>
Отличие заключается в том, что параметром является выходная лингвистическая переменная

Заключение
Для формирования базы нечетких продукций необходимо:
Определить входные и выходные лингвистические переменные
Определить шкалы их измерений
Построить терм-множество значений лингвистических переменных
Сформировать правила
Системы правил нечетких продукций позволяют не только получить более адекватное решение проблемы, но и менее строго относиться к противоречивости и полноте исходных правил