Уравнение прямой на плоскости

СОДЕРЖАНИЕ
Основные понятия
Уравнения прямой по точке и вектору нормали
Уравнение прямой проходящей через две точки
Уравнение прямой по точке и угловому коэффициенту
Уравнение прямой по точке и направленному вектору
Уравнение прямой в отрезках
Нормальное уравнение прямой
Угол между прямыми на плоскости
Уравнение прямой, проходящей через данную точку
перпендикулярно данной прямой
Расстояние от точки до прямой
Выводы
Кратка теория

Определение.
Любая прямая на плоскости может быть задана уравнением первого порядка
*причем постоянные А, В не равны нулю одновременно.
ОСНОВНЫЕ ПОНЯТИЯ
Ах + Ву + С = 0

Его называют общим уравнением. В зависимости от значений постоянных А,В и С возможны следующие частные случаи:
Уравнение прямой на плоскости может быть представлено в различном виде в зависимости от каких – либо заданных начальных условий.
X
y
• C = 0, А ≠0, В ≠ 0 – проходит через начало координат (рис.1)
Рис.1
• А = 0, В ≠0, С ≠0 { By + C = 0}- параллельна оси Ох(рис.2,а)
• В = 0, А ≠0, С ≠ 0 { Ax + C = 0} – параллельна оси Оу(рис.2,б)
Рис.2
y
X
• В = С = 0, А ≠0 – совпадает с осью Оу(рис.3,а)
• А = С = 0, В ≠0 – совпадает с осью Ох(рис.3,б)
а
б
X
y
Рис.3
а
б

УРАВНЕНИЕ ПРЯМОЙ ПО ТОЧКЕ И ВЕКТОРУ НОРМАЛИ
Определение. В декартовой прямоугольной системе координат вектор с координатами {А, В}. перпендикулярен прямой Ах + Ву + С = 0.
Пример . Найти уравнение прямой, проходящей через точку А(1, 2) перпендикулярно вектору n{3, -1}.
y
x
A
Решение. Составим при А = 3 и В = -1 уравнение: 3х – у + С = 0. Для нахождения коэффициента С подставим в полученное выражение координаты заданной точки А. Получаем: 3 – 2 + C = 0, следовательно, С = -1. Окончательно получим: 3х – у – 1 = 0.

УРАВНЕНИЕ ПРЯМОЙ, ПРОХОДЯЩЕЙ ЧЕРЕЗ ДВЕ ТОЧКИ
Если какой- либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель. Данное уравнение прямой м.б. записано:
y
x
.
.

УРАВНЕНИЕ ПРЯМОЙ, ПРОХОДЯЩЕЙ ЧЕРЕЗ ДВЕ ТОЧКИ
Пример. Найти уравнение прямой, проходящей через две точки А(1, 2) и В(3, 4).
x
y
.
.
Решение. Применяя записанную выше формулу, получаем:
А
B

УРАВНЕНИЕ ПРЯМОЙ ПО ТОЧКЕ И УГЛОВОМУ КОЭФФИЦИЕНТУ
Если общее уравнение прямой на плоскости Ах + Ву + С = 0 привести к виду:

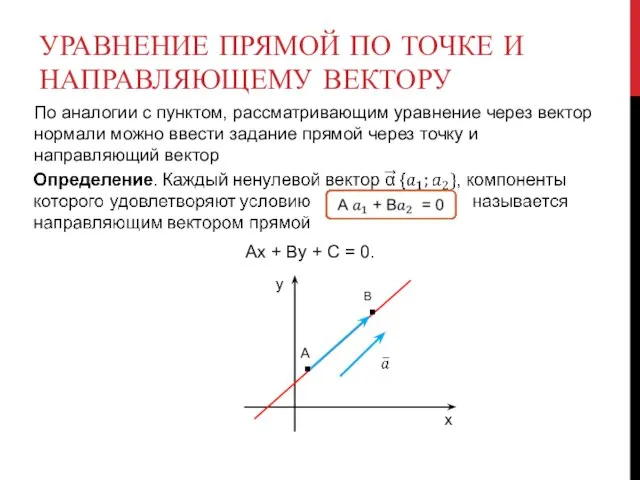
УРАВНЕНИЕ ПРЯМОЙ ПО ТОЧКЕ И НАПРАВЛЯЮЩЕМУ ВЕКТОРУ
По аналогии с пунктом, рассматривающим уравнение через вектор нормали можно ввести задание прямой через точку и направляющий вектор
Ах + Ву + С = 0.
.
.
x
y
A
B

Пример. Найти уравнение прямой, проходящей через точку А(1, 2) с направляющим вектором {1, -1}.
УРАВНЕНИЕ ПРЯМОЙ ПО ТОЧКЕ И НАПРАВЛЯЮЩЕМУ ВЕКТОРУ
.
x
y
A
Решение. Будем искать в виде: Ax + By + C = 0. В соответствии с определением, коэффициенты должны удовлетворять условиям:
1 * A + (-1) * B = 0, т.е. А = В.
Тогда получим вид: Ax + Ay + C = 0, или x + y + C / A = 0. при х = 1, у = 2 получаем С/ A = -3, т.е. искомое:
х + у - 3 = 0

УРАВНЕНИЕ ПРЯМОЙ В ОТРЕЗКАХ
Если в общем уравнении Ах + Ву + С = 0 С≠0, то, разделив на –С, получим:
или
Геометрический смысл коэффициентов в том, что коэффициент а является координатой точки пересечения прямой с осью Ох, а b – координатой точки пересечения с осью Оу.
, где
.
x
y
a
.
b
0

УРАВНЕНИЕ ПРЯМОЙ В ОТРЕЗКАХ
Пример . Задано общее уравнение х – у + 1 = 0. Найти его в виде уравнение прямой в отрезках.
С = 1, , а = -1, b = 1.
Решение.
.
x
y
a
.
b

НОРМАЛЬНОЕ УРАВНЕНИЕ ПРЯМОЙ
Если уравнение прямой на плоскости Ах + Ву + С = 0 умножить на число , ,которое называется
нормирующем множителем,
то получим
xcosφ + ysinφ - p = 0 –
нормальное уравнение. Знак ± нормирующего множителя надо выбирать так, чтобы μ * С < 0. р – длина перпендикуляра, опущенного из начала координат на
прямую, а φ - угол, образованный этим перпендикуляром с положительным направлением оси Ох.
x
y
0
φ
P

НОРМАЛЬНОЕ УРАВНЕНИЕ ПРЯМОЙ
Пример . Дано 12х – 5у – 65 = 0. Требуется написать различные типы уравнений этой линии.
Решение.
уравнение прямой в отрезках:
уравнение прямой с угловым коэффициентом: (делим на 5)
нормальное уравнение прямой:
cos φ = 12/13; sin φ= -5/13; p = 5.
;
Следует отметить, что не каждую прямую можно представить в отрезках, например, параллельные осям или проходящие через начало координат.

НОРМАЛЬНОЕ УРАВНЕНИЕ ПРЯМОЙ
Пример. Прямая отсекает на координатных осях равные положительные отрезки. Найти её, если площадь треугольника, образованного этими отрезками равна 8 см 2 .
Решение. Искомое уравнение имеет вид:
ab /2 = 8;
ab=16; a=4, a=-4. a = -4 < 0 не подходит по условию задачи
Итого:
или х + у – 4 = 0.

НОРМАЛЬНОЕ УРАВНЕНИЕ ПРЯМОЙ
Пример. Какая прямая проходит через точку А(-2, -3) и начало координат.
Решение. Имеем:
где х 1 = у 1 = 0; x2 = -2; y2 = -3.

УГОЛ МЕЖДУ ПРЯМЫМИ НА ПЛОСКОСТИ
Определение. Если заданы две прямые y = k1 x + b1 , y = k 2x + b2 , то острый угол между ними будет определяться как
Теорема. Ах + Ву + С = 0 и А 1 х + В1 у + С1 = 0 параллельны, когда пропорциональны коэффициенты А1 = λА, В1 = λВ. Если еще и С1 = λС, то они совпадают. Координаты точки пересечения находятся как решение системы этих уравнений.
x
y

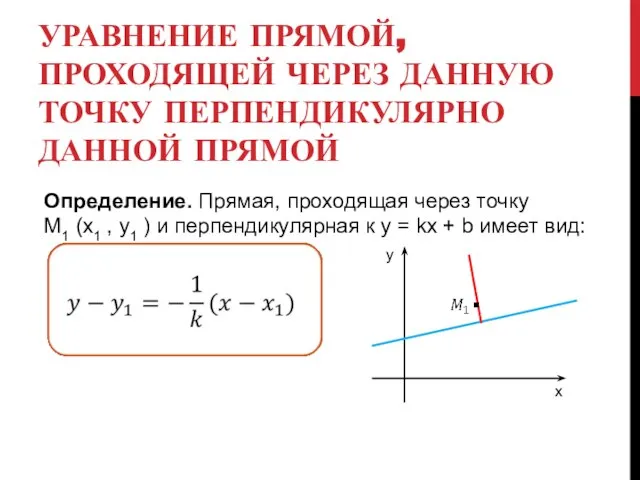
УРАВНЕНИЕ ПРЯМОЙ, ПРОХОДЯЩЕЙ ЧЕРЕЗ ДАННУЮ ТОЧКУ ПЕРПЕНДИКУЛЯРНО ДАННОЙ ПРЯМОЙ
Определение. Прямая, проходящая через точку М1 (х1 , у1 ) и перпендикулярная к у = kx + b имеет вид:
x
y
.

РАССТОЯНИЕ ОТ ТОЧКИ ДО ПРЯМОЙ
Теорема. Если задана точка М(х0 , у0 ), то расстояние до Ах + Ву + С =0 определяется как
Доказательство. Пусть точка М 1(х 1, у 1) – основание перпендикуляра, опущенного из точки М на заданную прямую. Тогда расстояние между точками М и М1 :
Координаты x1 и у1 могут быть найдены как решение системы уравнений:
(1)
x
y
.
M

РАССТОЯНИЕ ОТ ТОЧКИ ДО ПРЯМОЙ
Второе уравнение системы – это линия, проходящей через заданную точку М 0 перпендикулярно заданной прямой. Преобразовать первое к виду:
A(x – x 0 ) + B(y – y0 ) + Ax0 + By0 + C = 0,
то, решая, получим:
Подставляя эти выражения в (1), находим:
Теорема доказана.

РАССТОЯНИЕ ОТ ТОЧКИ ДО ПРЯМОЙ
Пример. Определить угол между: y = -3 x + 7; y = 2 x + 1.
Решение. k 1 = -3; k 2 = 2; tgφ =
; φ= π /4.

РАССТОЯНИЕ ОТ ТОЧКИ ДО ПРЯМОЙ
Пример. Показать, что 3х – 5у + 7 = 0 и 10х + 6у – 3 = 0 перпендикулярны.
Решение. Находим: k 1 = 3/5, k2 = -5/3, k 1* k 2 = -1, следовательно, они перпендикулярны.

РАССТОЯНИЕ ОТ ТОЧКИ ДО ПРЯМОЙ
Пример. Даны вершины треугольника А(0; 1), B (6; 5), C (12; -1). Найти высоту, проведенной из вершины С.
Решение. Находим сторону АВ:
;
4 x = 6 y – 6;
2 x – 3 y + 3 = 0;
Искомая высота имеет вид: Ax + By + C = 0 или y = =kx + b . k =
. Тогда y =
. Т.к. высота проходит
через точку С, то ее координаты удовлетворяют
данному уравнению:
откуда b = 17.
Итого:
Ответ: 3 x + 2 y – 34 = 0.

ВЫВОДЫ
Любое линейное уравнение является уравнением прямой.
Любая прямая задается уравнением первого порядка.
По линейному уравнению можно определить взаимное расположение прямых.

КРАТКАЯ ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Общее уравнение прямой
Частные случаи:

КРАТКАЯ ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Уравнение прямой «в отрезках»
Уравнение прямой с угловым коэффициентом
(A,B,C≠0 в общем уравнении прямой)
Частные случаи:

КРАТКАЯ ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Частные случаи:

Параметрические уравнения прямой
КРАТКАЯ ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
y
x
0
M

КРАТКАЯ ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
y
x
0
M

КРАТКАЯ ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
y
x
0
Уравнение прямой в нормальном вид