Нахождение угла между двумя прямыми в пространстве

Цели обучения
11.4.2 - находить угол между прямыми
(по заданным уравнениям прямых);

Цели урока
Уметь находить угла между двумя прямыми в пространстве

Каноническое уравнение прямой
Параметрическое уравнение прямой
Угол между двумя прямыми
Прямая в пространстве

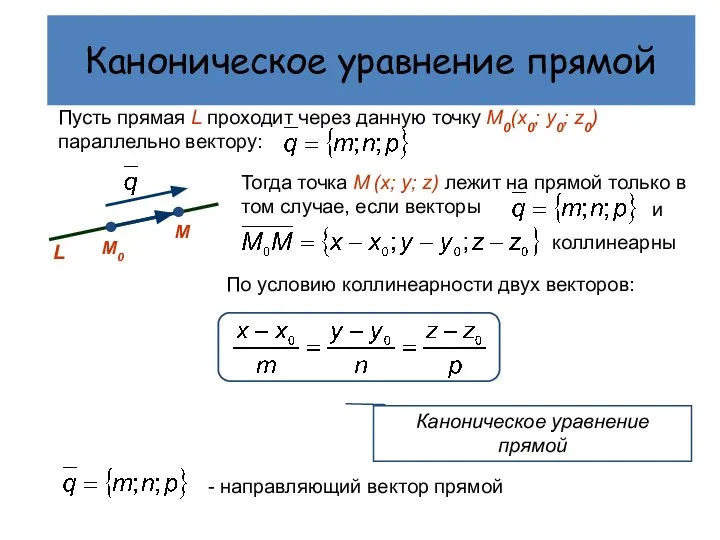
Пусть прямая L проходит через данную точку М0(x0; y0; z0) параллельно вектору:
Каноническое уравнение прямой
М0
L
М
Тогда точка М (x; y; z) лежит на прямой только в том случае, если векторы
и
коллинеарны
По условию коллинеарности двух векторов:
- направляющий вектор прямой
Каноническое уравнение прямой

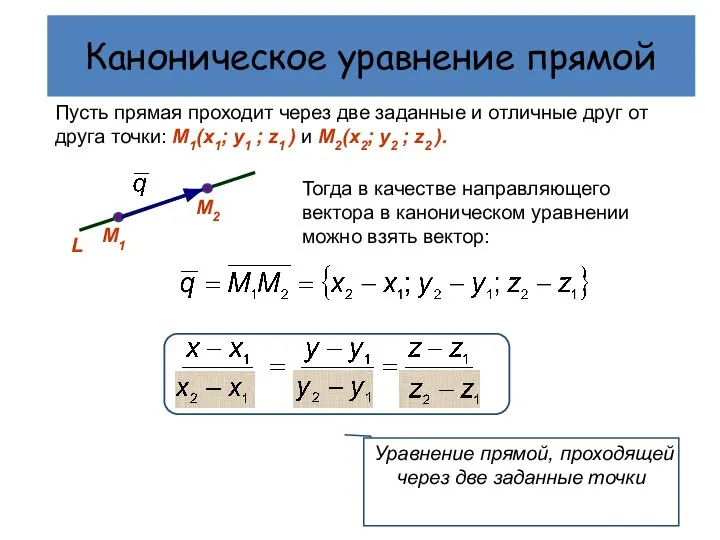
Каноническое уравнение прямой
Пусть прямая проходит через две заданные и отличные друг от друга точки: М1(х1; у1 ; z1 ) и М2(х2; у2 ; z2 ).
М1
М2
Тогда в качестве направляющего вектора в каноническом уравнении можно взять вектор:
Уравнение прямой, проходящей через две заданные точки
L
Каноническое уравнение прямой

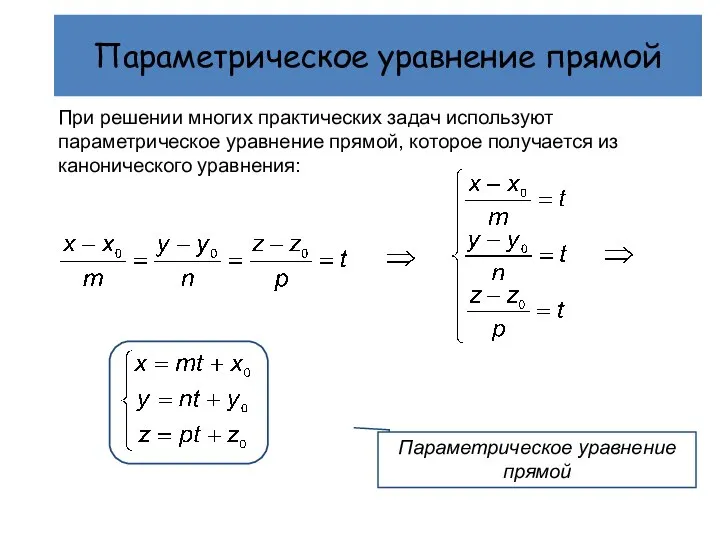
При решении многих практических задач используют параметрическое уравнение прямой, которое получается из канонического уравнения:
Параметрическое уравнение прямой
Параметрическое уравнение прямой

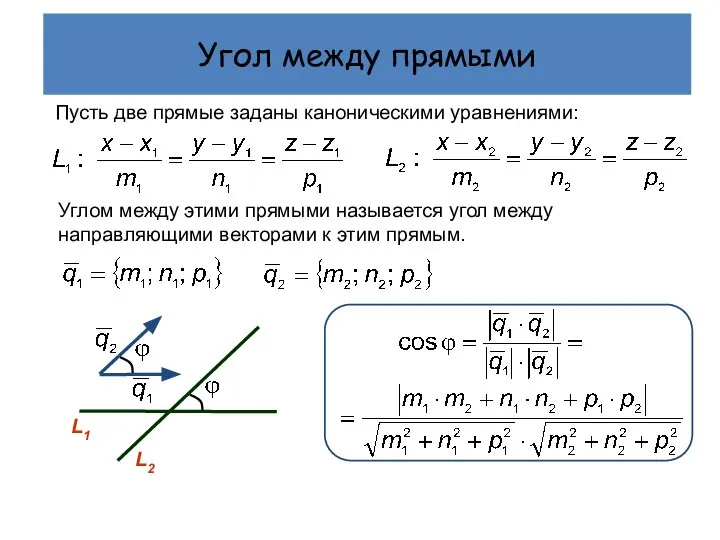
Угол между прямыми
Пусть две прямые заданы каноническими уравнениями:
Углом между этими прямыми называется угол между направляющими векторами к этим прямым.
L1
L2
Угол между прямыми

Пример:
Решение: Для решения этой задачи найдем направляющие векторы этих прямых. Уравнение первой прямой задано в канонической форме, поэтому направляющий вектор {3; 4; 5}. Преобразуем второе уравнение к каноническому вид.
Получено уравнение второй прямой в канонической форме:
{-2; -1/3; 2/3} - направляющий вектор второй прямой.

Решение задач