что это недостаток, так как 8 меньше 10. Делители числа 12 - 1, 2, 3, 4, 6. Их сумма равна 16, что считали избытком. А числа, у которых сумма делителей равна самому числу, особенно ценили и называли их совершенными. Так, совершенными числами являются числа 6 и 28, т.к.
6=1+2+3, 28=1+2+4+7+14.
Знаменитый греческий философ и математик Никомах Герасский, живший в 1 в., отмечал, что совершенные числа красивы, а красивые вещи редки и немногочисленны. Он не знал, сколько имеется совершенных чисел. Не знаем этого и мы. До настоящего времени неизвестно существуют ли нечетное и наибольшее чётное совершенные числа?
До сегодняшнего дня не обнаружено ни одного нечетного совершенного числа, хотя и не доказано, что такого числа не существует.
Совершенные числа









 Интегральные уравнения
Интегральные уравнения Как вычислить площадь поверхности тела человека
Как вычислить площадь поверхности тела человека Прямая и плоскость в пространстве. Смешанные задачи
Прямая и плоскость в пространстве. Смешанные задачи Система MatLab. Методические указания к выполнению лабораторных работ
Система MatLab. Методические указания к выполнению лабораторных работ Дискретная математика. Лекция 1. Введение
Дискретная математика. Лекция 1. Введение Презентация на тему Свойства четырехугольников
Презентация на тему Свойства четырехугольников  Пропорция
Пропорция Diskretnaya_matematika_sootvetstvia
Diskretnaya_matematika_sootvetstvia Правильные многоугольники
Правильные многоугольники Построение графика функции
Построение графика функции Правила комбинаторики. Решение комбинаторных задач
Правила комбинаторики. Решение комбинаторных задач Методика обучения решению простых задач
Методика обучения решению простых задач Пифагор. Жизнь и эпоха
Пифагор. Жизнь и эпоха Решение уравнений и неравенств. Задания для самостоятельной работы
Решение уравнений и неравенств. Задания для самостоятельной работы Свойства действий над числами
Свойства действий над числами Системы счисления
Системы счисления Решите систему неравенств и укажите все целые числа, которые являются ее решениями
Решите систему неравенств и укажите все целые числа, которые являются ее решениями Векторы
Векторы Решение уравнений третьей степени
Решение уравнений третьей степени Модуль числа. 6 класс
Модуль числа. 6 класс Признаки параллельности прямых
Признаки параллельности прямых Прямоугольный параллелепипед
Прямоугольный параллелепипед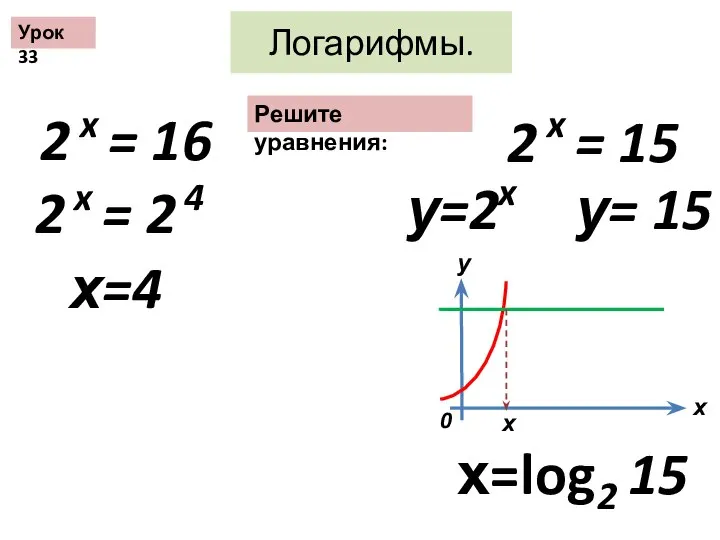 Логарифмы
Логарифмы Тригонометрия. Контрольная работа
Тригонометрия. Контрольная работа История развития математики
История развития математики Координаты вектора
Координаты вектора Сантиметр. Линейка
Сантиметр. Линейка Презентация на тему Физико-математический КВН в 9-х классах
Презентация на тему Физико-математический КВН в 9-х классах